动态规划之01背包
动态规划之01背包
1.什么是动态规划
动态规划是一种思想,是一种解决方法,并不是一种特定的算法。动态规划最重要的是状态和状态转移方程。是不是感觉还是听不懂这动态规划到底是啥?听起来就很牛皮,感觉完全学不会?其实并不是这么难理解,下面就结合一道例题来讲解一下https://vjudge.net/problem/POJ-3624
2.分析题意
有N种类型手镯,有着不同的属性,重量w和魅力值d,一个人想装备这些手镯,他有一个载重上限M,并且他想尽可能提高自己的魅力值,求最大的魅力值。
好了,现在让我们简单分析一下
- 装备一个手镯就会加魅力值和负重
- 要求魅力值最大,负重有一个上限,不同负重可能装备多种不同的手镯
2.1状态
那么,这题的状态是什么?我们通过上面的分析可以很简单地得出,状态就是不同负重下装备不同的手镯。我们怎么把不同的负重和不同类型手镯对应起来呢?我们可以很容易想到用一个二维数组,行是不同的负重,列是不同的手镯,行列对应的值代表当前的魅力值,这样就把所有的状态都存进来了。
ps.这里的列不是代表单纯只放这种类型手镯,而包括了前面放的手镯。
2.2状态转移
我们不妨令该数组为 D[M][N],对于D[M][N]来说,它的值有两种取值情况,一种是M的值小于w[N]的值,也就是当前负重不能放下第N个手镯,那么就有D[M][N]=D[M][N-1],也就是不放第N个手镯。另一种就是M的值大于w[N]的值,也就是可以放下第N个手镯,那么就有D[M][N]=D[M-w[N]][N-1]+d[N]。题目是求最大魅力值,那么转移方程也就出来了D[M][N]=max(D[M-w[N]][N-1]+d[N],D[M][N-1])。我们通过转移方程,可以发现,要想知道有N个手镯装备的魅力值,就要知道有N-1个手镯装备的魅力值,最终就归结到只有一个手镯的魅力值。
2.3图表分析
我们根据例题中的样例数据画出如下表格,记住,表格应该是从最底下那行开始往上画。
| 手镯类型\载重上限 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 4 | 7 | 12 | 16 | 19 | 23 |
| 2 | 0 | 7 | 12 | 13 | 19 | 19 |
| 3 | 0 | 7 | 12 | 12 | 19 | 19 |
| 4 | 0 | 7 | 7 | 7 | 7 | 7 |
我们可以很容易地从图中得知负重上限最大为6的时候,魅力值最大为23。
我们简单验证一下,对于D16,要看D25和D26,D25和D26都是19,但是D25+d1>D26,所以D16=19+4=23。
D25要看D35和D33,D33+d2=18,D35=19,故D25=19。
2.4简化
我们可以发现,要想知道当前层的情况,首先要知道下一层的情况,也就是二维数组其实可以用一维数组来代替。需要注意的一点是,如图
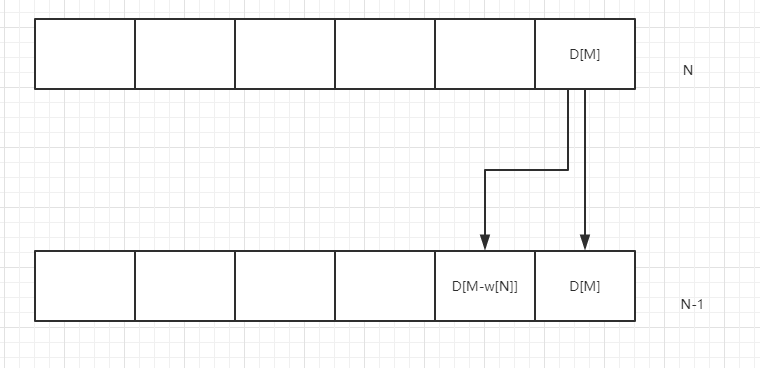
我们发现,上一行的值取决于下一行同一列的值或者前面的列的值。所以,计算该一维数组值的时候,应该从后往前计算。
3.AC代码
#include<iostream>
#include<string>
using namespace std;
int w[3500];
int v[3500];
int f[12900];
int max(int x, int y) {
return x > y ? x : y;
}
int main() {
memset(f, 0, sizeof(f));
memset(w, 0, sizeof(w));
memset(v, 0, sizeof(v));
int N, M;
while (cin >> N >> M) {
for (int i = 1; i <= N; i++) {
cin >> w[i] >> v[i];
}
for (int i = N; i >0; i--) {
for (int j = M; j > 0; j--) {
if (j >= w[i]) {
f[j] = max(f[j - w[i]] + v[i], f[j]);
}
}
}
cout << f[M] << endl;
}
return 0;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号