旋转数组

给你一个数组，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

提示：

1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
0 <= k <= 105

进阶：

尽可能想出更多的解决方案，至少有 三种 不同的方法可以解决这个问题。
你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？

解法1：新建另一数组temp，将nums数组复制到temp里面，在移位到nums

解法2：建立两个temp，一个存储当前i要移动的位置的数，一个存储当前i要移动的位置的数再移动的位置的数。需要考虑重复访问的问题。

有两种解决方案：①新建另一数组，如果某元素访问过，则标记；若下次遇到，直接跳过，下一个；

②找nums.length()与k之间的关系。据我目前的研究，对于len和k，需要进行gcd（len,k)次。

class Solution {
       public static int gcd(int q, int p)
       {
               if(p == 0)
                    {
                        return q;
                    }
                int r = q % p;
                return gcd(p,r);
       }
    public  void rotate(int[] nums, int k) {
           if(k!=0){
               int temp1;
               int temp2;
               int len = nums.length;
               int epoch;
               epoch = gcd(len, k);
               for(int i=0;i<epoch;i++){
                   temp1 = nums[i];
                   int j=(i+k)%len;
                   while(i!=j){
                       temp2 = nums[j];
                       nums[j] = temp1;
                       j = (j+k)%len;
                       temp1 = temp2;
                   }
                   nums[i] = temp1;
               }
           }
    }
}

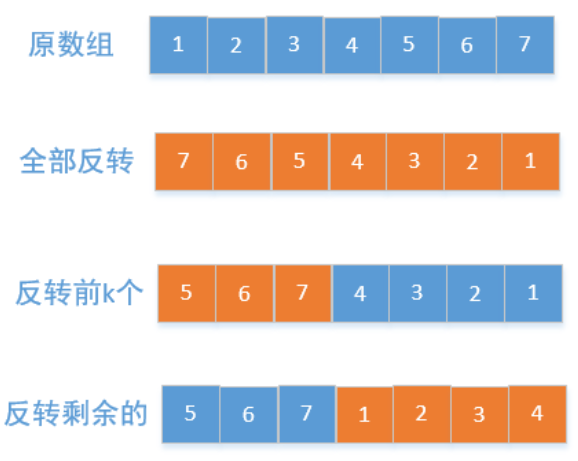
解法3. 第三种解法很巧妙。首先先翻转所有的数，再翻转前k个数，再翻转后k个数。大呼神奇！