五月集训（第27天）—图

目录

• 图
  • 1. 1791. 找出星型图的中心节点
  • 2. 797. 所有可能的路径
  • 3. 851. 喧闹和富有
  • 4. 959. 由斜杠划分区域

图

1. 1791. 找出星型图的中心节点

    思路：
        每条边都会连接中心结点，所以一条边的起点或者终点是中心结点。

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        int a = edges[0][0];
        if (a == edges[1][0] || a == edges[1][1]) {
            return a;
        }
        return edges[0][1];
    }
};

2. 797. 所有可能的路径

    思路：
        从起点0开始深搜，搜到点n-1保存答案路径，回到上一点再搜，直到找到图上所有到达n-1的路径。

class Solution {
    vector<vector<int>> ans;
    vector<int> temp;

    void dfs(int s, vector<vector<int>> &graph, int n) {
        int m = graph[s].size(), i;
        if (s == n - 1) {   /* 递归出口是搜到点 n - 1 保存答案 */
            ans.push_back(temp);
            return ;
        }

        for (i = 0; i < m; ++i) {   /* 回溯遍历 */
            temp.push_back(graph[s][i]);
            dfs(graph[s][i], graph, n);
            temp.pop_back();
        }
    }
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        int graph_size = graph.size();
        ans.clear();
        temp.clear();
        temp.push_back(0);
        dfs(0, graph, graph_size);
        return ans;
    }
};

3. 851. 喧闹和富有

    思路：
        利用richer数组建图：从一个人指向比自己富的人。
        从每个人出发，遍历每个可达结点，即比自己富的人，记录quiet最小的人为答案。（起始值设为自己）
        注意：每次从一个人出发，利用hash[]标记遍历过的结点，如果dfs中发现遍历过的结点，则直接返回。按理说n<=500且没有环,应该不会超时，但是不加hash[]就TLE，不理解，QAQ

class Solution {
    int hash[501];
    void dfs(int s, vector<vector<int>> &graph, vector<int> &ans, vector<int> &quiet, int pos_s) {
        if (hash[s]) return;
        hash[s] = 1;
        int m = graph[s].size(), i;
        if (m == 0) return ;
        for (i = 0; i < m; ++i) {
            if ( quiet[ graph[s][i] ] < quiet[ ans[pos_s] ] ) {
                ans[pos_s] = graph[s][i];
            }
            dfs(graph[s][i], graph, ans, quiet, pos_s);
        }
    }
public:
    vector<int> loudAndRich(vector<vector<int>>& richer, vector<int>& quiet) {
        vector<int> ans;
        int n = quiet.size();
        int richer_size = richer.size(), i;
        vector<vector<int>> graph (n);
        for (i = 0; i < n; ++i) ans.push_back(i);

        for (i = 0; i < richer_size; ++i) {
            graph[richer[i][1]].push_back(richer[i][0]);
        }

        for (i = 0; i < n; ++i) {
            memset(hash, 0, sizeof(hash));
            dfs(i, graph, ans, quiet, i);
        }
        return ans;
    }
};

4. 959. 由斜杠划分区域

    思路：
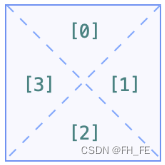
        两中方向的斜杠可以把一个方格划分为0，1，2，3四个区域，利用并查集对区域进行操作即可得连通块得数目。
        每个方块向右将当前方块的1区和右边方块得3区连通
        每个方块向下将当前方块的3区和下边方块得0区连通
        '/'将每个方块内的0区和3区，1区和2区连通
        '\\'将每个方块内的0区和1区，2区和3区连通
        ' '将每个方块内的0区,1区****2区,3区全部连通

class Solution {
    // 将一个方格分为上下左右四个三角形，并把二维网络压成一维，数组长度为 4 * n * n
    #define N 3610
    int F[N];
    int count;

    void union_find_init(int n) {
        int len = 4 * n * n, i;
        count = len;
        for (i = 0; i < len; ++i) F[i] = i;
    }

    void union_set(int a, int b) {
        int fa = find_f(a);
        int fb = find_f(b);
        if (fa == fb) return ;
        F[fa] = fb;
        count--;
    }

    int find_f(int x) {
        if (x == F[x]) return x;
        return F[x] = find_f(F[x]);
    }

public:
    int regionsBySlashes(vector<string>& grid) {
        int n = grid.size();
        union_find_init(n);
        int index = 0, i, j;

        for (i = 0; i < n; ++i) {
            for (j = 0; j < n; ++j) {
                int rect = i * n + j;
                int rect_right = i * n + j + 1;
                int rect_down = (i + 1) * n + j;
                if (i < n - 1) union_set((rect << 2) | 2, ((rect_down) << 2) | 0);     // 合并上面方格的2和下面方格的0
                if (j < n - 1) union_set((rect << 2) | 1, (rect_right << 2) | 3 );      // 合并左边方格的1和右边方格的3

                if (grid[i][j] == ' ') {            /* 空格则合并四个小三角 */
                    union_set((rect << 2) | 0, (rect << 2) | 1);
                    union_set((rect << 2) | 0, (rect << 2) | 2);
                    union_set((rect << 2) | 0, (rect << 2) | 3);
                } else if (grid[i][j] == '/') {     /* '/'则合并0，3和1，2区域 */
                    union_set((rect << 2) | 0, (rect << 2) | 3);
                    union_set((rect << 2) | 1, (rect << 2) | 2);
                } else {                            /* '\\'则合并0，1和2，3区域 */
                    union_set((rect << 2) | 0, (rect << 2) | 1);
                    union_set((rect << 2) | 2, (rect << 2) | 3);
                }
            }
        }
        return count;
    }
};