匀变速直线运动的规律
匀变速直线运动的规律
一、定义:匀变速直线运动为沿一条直线且加速度恒定不变的运动,在 \((v-t)\) 图中,其表示为一条倾斜的直线。
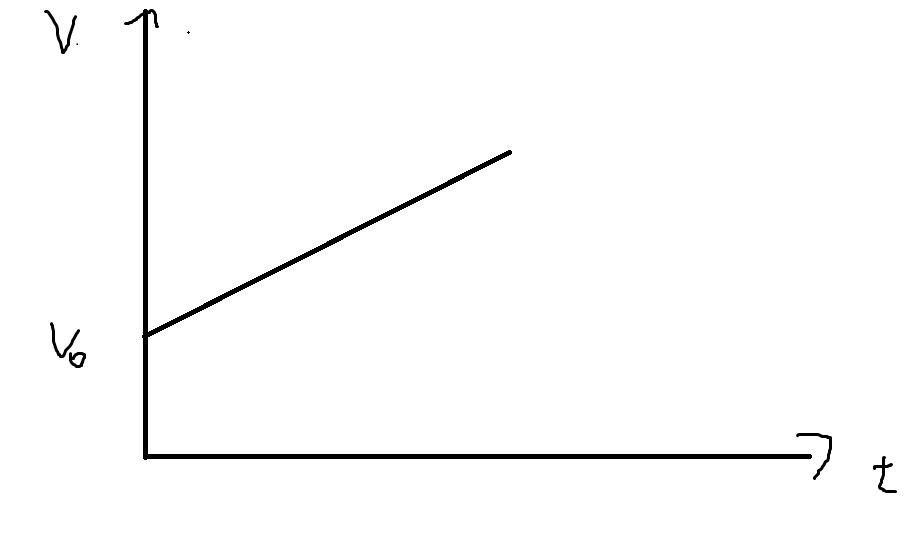
二、关于字母的解释:\(v_0\) 表示初始速度,\(v_t\) 表示末速度,\(t\) 表示时间,\(a\) 表示加速度,\(s\) 代表位移。
三、关于匀变速直线运动的公式。
物体的加速度等于物体速度的变化 \((\Delta v=v_t-v_0)\) 与发生这一变化所用时间 \(t\) 之比,用符号 \(a\) 来表示,即:\(a=\dfrac{v_t-v_0}{t}\),其表示为加速度定义式。
匀变速直线运动的基本规律:
\((1)\) 速度与时间关系式:\(v_t=v_0+at\),(这是由加速度定义式变形得来的)
\((2)\) 利用图像得到的公式:\(s=\dfrac{v_0+v_t}{2}×t\),(实际上就是\(s=\overline{v}t\),如下图,求梯形面积)
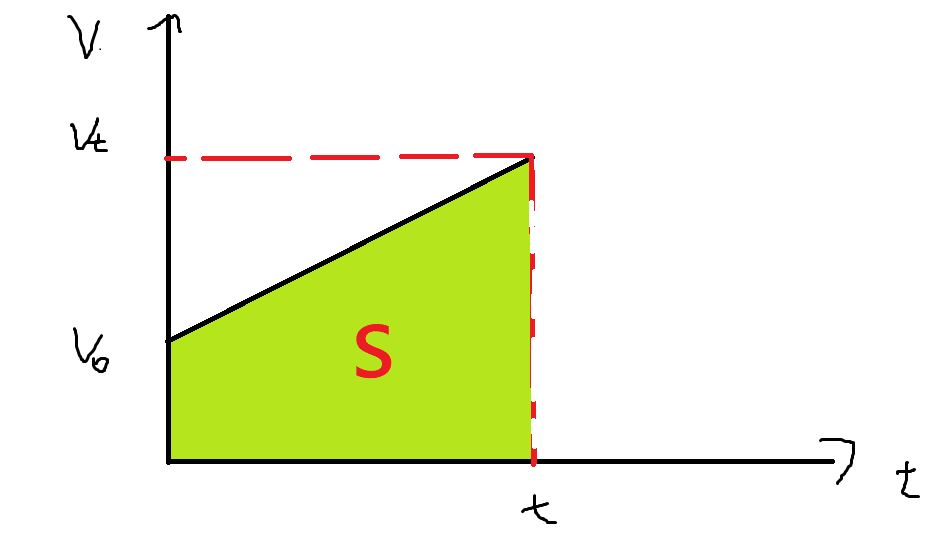
现在我们来推个公式
将 \((1)\)代入 \((2)\):
\(s=\dfrac{v_0+(v_0+at)}{2}×t\)
\(s=\dfrac{2v_0+at}{2}×t\)
\(s=v_0t+\frac{1}{2}at^2\)
这就是匀变速直线运动位移随时间变化的关系,称为匀变速直线运动的位移公式。
接下来我们用 \(\begin{cases}v_t=v_0+at①\\s=v_0t+\frac{1}{2}at^2②\end{cases}\) 来推出新式子
将\(①\)两边平方:\(v_t^2=v_0^2+2v_0at+a^2t^2\)
移项:\(v_t^2-v_0^2=2v_0at+a^2t^2\)
合并同类项:\(v_t^2-v_0^2=a(2v_0t+at^2)\)
发现此时的 \((2v_0t+at^2)\) 与 \(②\) 很像,就是两倍关系!
所以将 \(②\) 代入:\(v_t^2-v_0^2=2as\)
这就是速度与位移的关系式。
最后我们再推一个式子,还是用 \(\begin{cases}v_t=v_0+at①\\s=v_0t+\frac{1}{2}at^2②\end{cases}\) 来推
将 \(①\) 变形得到:\(v_0=v_t-at③\)
将 \(②\) 也变形:\(s=(v_0+\frac{1}{2}at)×t\)
将 \(\frac{1}{2}at\) 变成 \(at-\frac{1}{2}at\):\(s=(v0+at-\frac{1}{2}at)×t\)
将 \(③\) 代入 \(②\):\(s=[(v_t-at)+at-\frac{1}{2}at]×t\)
合并一下:\(s=v_tt-\frac{1}{2}at^2\)
这也是一个关系式。
总结一下:每个公式都有各自的优势,依据已知的条件选择恰当的公式。
| 公式 | 需要的物理量(任意三个即可套用) |
|---|---|
| \(s=\dfrac{v_0+v_t}{2}×t\) | \(s,v_0,v_t,t\) |
| \(s=v_0t+\frac{1}{2}at^2\) | \(s,v_0,a,t\) |
| \(v_t^2-v_0^2=2as\) | \(s,v_0,v_t,a\) |
| \(s=v_tt-\frac{1}{2}at^2\) | \(s,v_t,a,t\) |
| \(v_t=v_0+at\) | \(v_0,v_t,a,t\) |
四、匀变速直线运动的推论及应用。
详细见匀变速直线运动的推论,建议画图加深理解




 浙公网安备 33010602011771号
浙公网安备 33010602011771号