20230803

数论

筛素数

素数的定义: 只有1和它本身两个因数。

埃式筛

核心思想:如果一个数\(n\)能被\(\left ( 1,n \right )\)中的数整除, 那么这个数就不是素数.

bool check(long long num) {
    if (num == 1) {
        return false;
    }
    for (long long i = 2; i * i <= num; i++) {
        if (num % i == 0) {
            return false;
        }
    }
    return true;
}

线性筛

核心思想: 如果一个数\(n\)不是\(\left ( 1,n \right )\)中任意一个数的倍数, 那么\(n\)为素数, 所有n的倍数不是素数.

for (int i = 2; i < N; i++) {
        if (visNum[i] == 0) {
            primeCnt++;
            prime[primeCnt] = i;
        }
        for (int j = 1; j <= primeCnt && prime[j] * i < N; j++) {
            visNum[prime[j] * i] = true;
            if (i % prime[j] == 0) {
                break;
            }
        }
    }

排列组合

排列

排列\(n\)个不同的数，请问有多少种排列方式?

第一个数可以是有\(n\)种选择, 第二个数有\(n-1\)种选择, 第三个数有\(n-2\)种选择, 第\(i\)个数有\(n-i+1\)种选择, \(n\)个不同的数的排列就是\(n\times \left ( n-1 \right )\times \left ( n-2 \right ) \times \left ( n-3 \right ) \cdots \times 2 \times 1\)种方式, 也就是\({\large A^{n}_{n}}\) 种排列方式

共\(n\)个不同的数, 从中选\(m\)个数排列, 共有多少种排列方式?

与全部选择不同, 只需要选择到第\(m\)个数就是就可以, 就是\(n\times \left ( n-1 \right )\times \left ( n-2 \right ) \times \left ( n-3 \right ) \cdots \times \left ( n-m+2 \right ) \times \left ( n-m+1 \right )\), 也就是\({\large A^{m}_{n}}\)种选择方式

组合

有\(n\)个不同的数, 从中选取\(m\)个数, 请问有多少种选取方式?

首先计算出从\(n\)个数中选择\(m\)个数共有多少种有序的方式, 然后除去数字相同但是顺序不同的情况, 也就是\({\Large \frac{A^{m}_{m}}{A^{m}_{n}}}\)种方式, 也就是\({\large C^{m}_{n}}\)种方式

---

排列和组合的区别在于, 排列对顺序有要求, 组合对顺序没有要求

123和321在排列中被看作是两种情况, 而在组合中被看作是一种情况.

转换思维

\(n\)个不同的人排队, 其中有两个人必须站在一起, 问有多少种排列方式?

将两个人视作同一个人排列, 然后再考虑这两个人的站位问题, ${\Large A_{n-1}^{n-1} \times A_{2}^{2}} $.

球棍模型

将\(n\)个人分进\(m\)个不同的班级中, 请问有多少种方式? (可以有班级没有学生)(数据保证\(m < n\))

举例:
\(n = 5 , m = 3\)
将每个人看作一个球

将分班看作一根棍,
比如可以将1分进1班/23分进2班/45分进3班

又因为可以有班级没有学生, 那么棍子可以在球的最左边和最右边,

也就是所有学生都进了二班.
综上问题转换为在\(5+1=6\)个空隙中放入\(3-1=2\)根棍子, 共有多少种方式.
也就是在\(n+1\)个空隙中放入\(m-1\)根棍子, 共有多少种方式.
因为棍子和棍子没有区别, 所以是组合而不是排序
也就是\({\large C_{n+1}^{m-1}}\)

将\(n\)个人分进\(m\)个不同的班级中, 保证每个班级至少有一名学生, 请问有多少种方式? (数据保证\(m < n\))

整体思路和上题相同, 但因为每个班级至少有一名学生, 所以棍子不可以放在最左和最右, 也就是共有\(n-1\)个空隙,答案为\({\large C_{n-1}^{m-1}}\)

快速幂

OI-WIKI链接

模板:

long long binpow(long long a, long long b) {
    long long res = 1;
    while (b > 0) {
        if (b & 1) res = res * a;
        a = a * a;
        b >>= 1;
    }
    return res;
}

题目描述
监狱有 n 个房间，每个房间关押一个犯人，有 m 种宗教，每个犯人会信仰其中一种。如果相邻房间的犯人的宗教相同，就可能发生越狱，求有多少种状态可能发生越狱。

答案对 100,003 取模。

输入格式
输入只有一行两个整数，分别代表宗教数 m 和房间数 n。

输出格式
输出一行一个整数代表答案。

输入输出样例
输入

2 3

输出

6

说明/提示
样例输入输出 1 解释

状态编号	1号房间	2号房间	3号房间
1	信仰 1	信仰 1	信仰 1
2	信仰 1	信仰 1	信仰 2
3	信仰 1	信仰 2	信仰 2
4	信仰 2	信仰 1	信仰 1
5	信仰 2	信仰 2	信仰 2
6	信仰 2	信仰 2	信仰 1

数据规模与约定
对于 100% 的数据，保证1≤m≤108，1≤n≤1012。

所有可能性数量和两两相邻两个不同的数量相减, 剩下的就是相邻两个相同的数量. 第一个有\(m\)种选择, 第二个人和第一个人不同, 所以\(m-1\)种选择, 第三个人和第二个人不同, 但可以和第一个人相同, 所以也有\(m-1\)种选择, 以此类推, 除第一个人外剩下\(n-1\)个人都有\(m-1\)种选择

#include <bits/stdc++.h>

using namespace std;

const int MOD = 100003;

long long f(long long a, long long b) {//快速幂
    long long x = 1, y = a;
    while (b >= 1) {
        if (b % 2 == 1) {
            x = x * y % MOD;
        }
        y = y * y % MOD;
        b /= 2;
    }
    return x;
}

int main() {
    long long n;
    long long m;
    cin >> m >> n;
    cout << (f(m, n) - (m * f(m - 1, n - 1)) % MOD + MOD) % MOD;
    return 0;
}

图论

图

有向图

边有方向的就是有向图.

连通图: 图中任意两点间均有边.

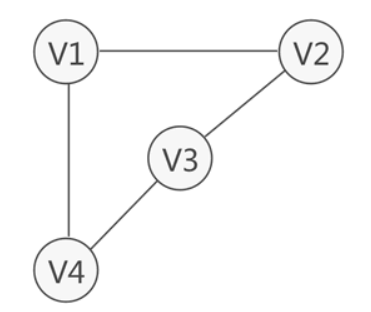
强连通图: 图中任意两点均可相互到达.

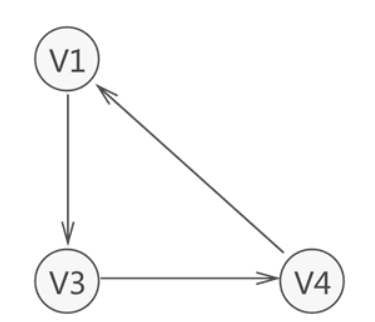
连通分量: 图中为连通图的部分.

强连通分量: 图中为强连通的部分.

无向图

将边视作双向边, 可变成有向图.

树

• 树是一种有向无环图.
• 树的根节点入度为0; 其他结点入度为1.