[杂题]URAL2047. Maths

题意：构造一个长度为n的串，使得 除了第一个以外，每个位置的前缀和的因子个数恰好等于该位置上的数。

n$\le 100000$

举个例子$a_i$：2   4    6     6    4    8    4    8    4   8

    前缀和   ：     6   12   18   22  30  34  42  46  54

6的因子：1 2 3 6 为4个  等于a[2]

12的因子：1 2 3 4 6 12 为6个  等于a[3]

18的因子：1 2 3 6 9 18 为6个  等于a[4]

...

...

54的因子：1 2 3 6 9 18 27 54 为8个 等于a[9]

 

所有都满足，则该列合法

 

一开始一直在想到哪儿为止会Impossible

然后就打算暴力一发 看到哪儿为止

后来发现正着写，根本写不出来。

于是发现把每个数的因子数写出来，倒着减回去，

每个数回去都只有一条路，最长的就是答案。

比如

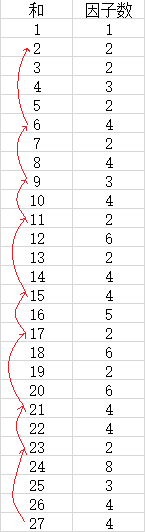
27这个数回去 长度为9

26这个数回去 长度为6

...

每个数回去都有一个长度

 

后来发现只需知道 “那个数减去因子个数” 的 那个数 回去有多长+1就好啦

那只要预处理一下因子个数

正着for一遍，O(1)就能得到长度

 

(for的是 和 ， 长度就是题目输入的n ， 需要输出的是 长度最长的那一串回去的路上的数的因子数)

 

那么打个这样的表，只需1秒钟

int phi[20000005];
int pri()
{
    memset(phi, 0, sizeof(phi));
    for(int i=2;i<=2000000;i++)
        for(int j=i;j<=2000000;j+=i)
            phi[j]++;
}

int dp[20000005];
void pre()
{
    memset(dp, 0, sizeof(dp));
    dp[1]=1, dp[2]=1;
    for(int i=3;i<=2000000;i++)
    {
        int num=phi[i]+1;
//        if(num>300 || dp[i-num]==-1)
//            dp[i]=-1;
//        else
            dp[i]=dp[i-num]+1;
//        printf("%d %d\n", i, dp[i]);
        if(dp[i]>=100000)
        {
            printf("%d %d\n", i, dp[i]);
            break;
        }
    }
}

int main()
{
//    freopen("out.txt", "w", stdout);
    pri();
    pre();
    return 0;
}

 

得到的这个1568617就是n为100000的最后一个数

 

要得到n个数，倒着减回去就好了

 

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PI;
const int N=1e5+5;
const double eps=1e-5;
const int mod=1e9+7;

int ans[100005], d;
int phi[1568625];
void pre()
{
    memset(phi, 0, sizeof(phi));
    for(int i=2;i<=1568617;i++)
        for(int j=i;j<=1568617;j+=i)
            phi[j]++;
    int x=1568617;
    d=0;
    while(x)
    {
        ans[d++]=x;
        int num=phi[x]+1;
        x-=num;
    }
}

int main()
{
    pre();
    int n;
    while(~scanf("%d",&n))
    {
        int sum=0;
        for(int i=d-1, j=1;j<=n;j++, i--)
        {
            printf("%d", ans[i]-sum);
            sum=ans[i];
            if(j==n)
                puts("");
            else
                putchar(' ');
        }
    }
    return 0;
}