【2011集训贾志鹏】Crash 的数字表格

题面

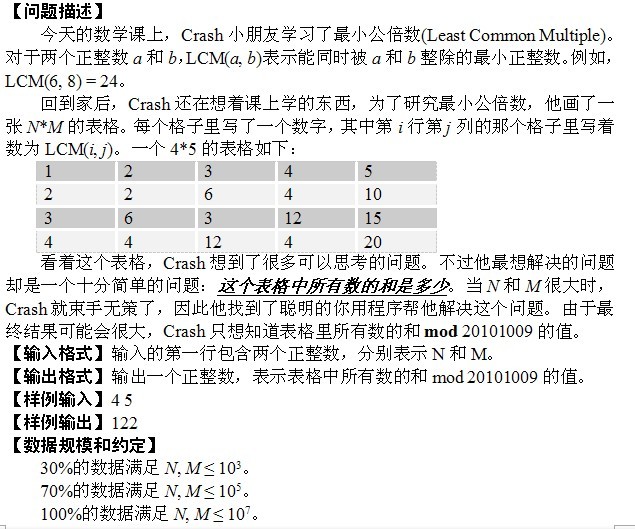
题目分析

（默认\(n<m\)）

题目要求\(\sum\limits_{i=1}^n\sum\limits_{j=1}^mlcm(i,j)\)。

由\(lcm(i,j)=\frac{i\cdot j}{gcd(i,j)}\)

得:

\[\begin{split} ans & =\sum\limits_{i=1}^n\sum\limits_{j=1}^m\frac{i\cdot j}{gcd(i,j)} \\ & =\sum\limits_{d=1}^n\sum\limits_{i=1}^n\sum\limits_{j=1}^m\frac{i\cdot j}{d}[gcd(i,j)==d]\\ & = \sum\limits_{d=1}^nd\cdot \sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}i\cdot j[gcd(i,j)==1] \end{split} \]

如果只看最后一部分，\(\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}i\cdot j[gcd(i,j)==1]\)，可以很自然想到莫比乌斯反演。

---

（以下\(n,m,gcd\)为\(\lfloor\frac n d\rfloor,\lfloor\frac m d \rfloor,\lfloor\frac {gcd}d\rfloor\)）

我们用\(g(i)\)表示\(gcd(i,j)==k\cdot i,k\in Z\)的贡献，\(f(i)\)表示\(gcd(i,j)==i\)的贡献。

于是有\(g(x)=\sum\limits_{x|d}^nf(d) \Rightarrow f(x)=\sum\limits_{x|d}^n\mu(\frac d x)\cdot g(d)\)。

只要可以快速求出\(g(d)\)便可得到答案。

对于\(g(x)\)：

\[\begin{split} g(x)&=\sum\limits_{i=1}^n\sum\limits_{j=1}^mi\cdot j[x|gcd(i,j)]\\ &=x\cdot x\cdot \sum\limits_{i=1}^{\lfloor\frac{n}{x}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{x}\rfloor}i\cdot j[1|gcd(i,j)]\\ &=x\cdot x\cdot \sum\limits_{i=1}^{\lfloor\frac{n}{x}\rfloor}i\sum\limits_{j=1}^{\lfloor\frac{m}{x}\rfloor}j\\ &=x\cdot x\cdot \frac{(1+\lfloor\frac{n}{x}\rfloor)\cdot \lfloor\frac{n}{x}\rfloor}{2}\cdot \frac{(1+\lfloor\frac{m}{x}\rfloor)\cdot \lfloor\frac{m}{x}\rfloor}{2} \end{split} \]

---

最终

\[\begin{split} ans &=\sum\limits_{d=1}^n d\cdot f(1)\\ &=\sum\limits_{d=1}^n d\cdot \sum\limits_{i=1}^{\lfloor\frac n d\rfloor}\mu(i)\cdot g(i)\\ \end{split} \]

你会发现，现在的时间复杂度还是有问题，这时候就需要整除分块求解。

P.S

加强版：【BZOJ2693】jzptab

代码实现

#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdio>
#include<iomanip>
#include<cstdlib>
#define MAXN 0x7fffffff
typedef long long LL;
const int N=1e7+5,mod=20101009;
using namespace std;
inline int Getint(){register int x=0,f=1;register char ch=getchar();while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}return x*f;}
int mu[N],prime[N],g[N];
bool vis[N];
int t(int x){return 1ll*x*(x+1)/2%mod;}
int f(int n,int m){
	if(n>m)swap(n,m);
	LL ans=0;
	for(int l=1,r;l<=n;l=r+1){
		r=min(n/(n/l),m/(m/l));
		ans=(ans+1ll*(g[r]-g[l-1])*t(n/l)%mod*t(m/l)%mod)%mod; 
	}
	return ans;
}
int main(){
	mu[1]=g[1]=1;
	for(int i=2;i<=1e7;i++){
		if(!vis[i])prime[++prime[0]]=i,mu[i]=-1;
		for(int j=1;j<=prime[0]&&1ll*i*prime[j]<=1e7;j++){
			vis[i*prime[j]]=1;
			if(i%prime[j]==0)break;
			mu[i*prime[j]]=-mu[i];
		}
		g[i]=(g[i-1]+1ll*i*i*mu[i]%mod)%mod;
	}
	
	int n=Getint(),m=Getint();
	if(n>m)swap(n,m);
	LL ans=0;
	for(int l=1,r;l<=n;l=r+1){
		r=min(n/(n/l),m/(m/l));
		ans=(ans+1ll*(l+r)*(r-l+1)/2%mod*f(n/l,m/l)%mod)%mod;
	}
	cout<<(ans+mod)%mod;
	return 0;
}