杜教筛

积性函数

如果一个数论函数\(f(n)\)，满足\(n,m\)互质，那么有\(f(n*m) = f(n)*f(m)\)，那么\(f(n)\)为积性函数

特别地，如果对于任意\(n,m\)都满足\(f(n*m) = f(n)*f(m)\),那么\(f(n)\)为完全积性函数

常见的积性函数有

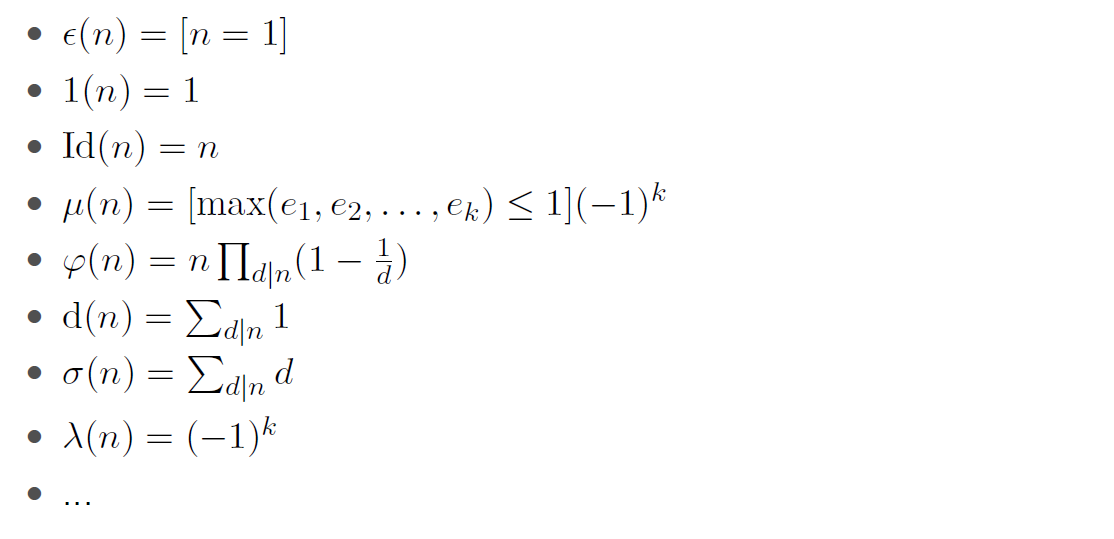
狄利克雷卷积

对于两个积性函数\(f(n),g(n)\)，定义它们的狄利克雷卷积为:\((f*g)(n) = \sum_{d|n} f(d) * g(\frac{n}{d})\)

常用的几种卷积关系：

$\mu * 1 = \epsilon $

\(\phi * 1=Id\quad \quad\varphi = Id * \mu\)

\(d = 1 * 1\quad \quad 1 = \mu*d\)

杜教筛

以低于线性的时间复杂度计算积性函数前缀和

假设要求的积性函数\(f\)的前缀和为\(S\)

构造两个辅助函数:积性函数\(g\),狄利克雷卷积\(f*g\)

有结论\(\sum_{i = 1}^n(f*g)(i) = \sum_{i = 1}^ng(i)S(\frac{n}{i})\)

变式:

\[g(1)S(n) = \sum_{i = 1}^n(f*g)(i) - \sum_{i = 2}^ng(i)S(\frac{n}{i}) \]

只需要找到一个\(g(n)\)使得\(\sum_{i = 1}^n(f*g)(i)\)可以被快速计算，且\(g(n)\)的前缀和容易求

那么可以分块+递归求出\(S(n)\)

莫比乌斯函数前缀和

\(S(n) = \sum_{i= 1}^n\mu(i)\)

\(g(1)S(n) = \sum_{i = 1}^n(f*g)(i) - \sum_{i = 2}^ng(i)S(\frac{n}{i})\)

选择\(g = 1(i)\)，那么对于\((f*g)(i) = \sum_{d|i}1*\mu(\frac{i}{d}) = \epsilon\)

又\(\sum_{j|i}\mu(j)= \left\{\begin{array}{ll} 0 & i \geq 2 \\ 1 & i=1 \end{array}\right.\)

\(S(n) = 1 - \sum_{i = 2}^nS(\lfloor\frac{n}{i}\rfloor)\)

欧拉函数前缀和

\(S(n) = \sum_{i = 1}^n\varphi(i)\)

\(g(1)S(n) = \sum_{i = 1}^n(f*g)(i) - \sum_{i = 2}^ng(i)S(\frac{n}{i})\)

选择\(g = 1(i)\)，那么对于\((f*g)(i) = \sum_{d|i}1 * \varphi(\frac{i}{d}) = Id\)

又\(\sum_{i = 1}^nId = \frac{n(n+1)}{2}\)

\(S(n) = \frac{n(n+1)}{2} - \sum_{i=2}^nS(\lfloor\frac{n}{i}\rfloor)\)

模板

#include <iostream>
#include <cstdio>
#include <unordered_map>
#define ll long long
using namespace std;
const int N = 3e6 + 5;
bool vis[N];
ll phi[N], mu[N], pri[N];
int tot = 0;
unordered_map<int,ll> ans_p, ans_m;
void table(int N){
    mu[1] = 1, phi[1] = 1; vis[1] = vis[0] = 1;
    for(int i = 2; i < N; i++){
        if(!vis[i]){
            pri[++tot] = i;
            mu[i] = -1;phi[i] = i - 1;
        }
        for(int j = 1; j <= tot; j++){
            if(i * pri[j] > N)break;
            vis[i * pri[j]] = 1;
            if(i % pri[j] == 0){
                mu[i * pri[j]] = 0;
                phi[i * pri[j]] = phi[i] * pri[j];
                break;
            }else{
                mu[i * pri[j]] = -mu[i];
                phi[i * pri[j]] = phi[i] * phi[pri[j]];
            }
        }
    }
    for(int i = 1; i <= N; i++){
        phi[i] += phi[i - 1];
        mu[i] += mu[i - 1];
    }
}
ll sum_p(int n){
    if(n <= N) return phi[n];
    if(ans_p[n]) return ans_p[n];
    ll ans = (ll)n * (n + 1) / 2;
    for(int l = 2, r; l <= n; l = r + 1){
        r = n / (n / l);
        ans -= sum_p(n / l) * (r - l + 1);
    }
    return ans_p[n] = ans;
}
ll sum_m(int n){
    if(n <= N) return mu[n];
    if(ans_m[n]) return ans_m[n];
    ll ans = 1;
    for(int l = 2, r; l <= n; l = r + 1){
        r = n / (n / l);
        ans -= sum_m(n / l) * (r - l + 1);
    }
    return ans_m[n] = ans;
}
int main(){
    table(N);
    int n;
    scanf("%d",&n);
    printf("%lld %lld\n", sum_m(n), sum_p(n));
    return 0;
}

mini筛