ST表--适用多查询O(1)

ST表类似树状数组，线段树这两种算法，是一种用于解决RMQ问题的离线算法。

预处理\(O(nlogn)\)，查询\(O(1)\)

给出一个长度为\(N\)的数列，和\(M\)次查询，求出每一次询问的区间内数字的最大值

定义：

\(st[i][j]\)表示从\(i\)位置开始的\(2^j\)个数中的最大值，即\(st[i][j] = max(a_i,...a_{i + 2^j-1})\)

预处理

\(O(nlogn)\)

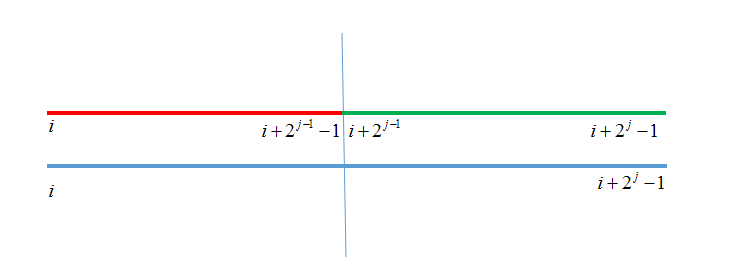
把\(st[i][j]\)对应的\([i,i + 2^j - 1]\)分成\([i,i + 2^{j - 1} - 1]\)和\([i+2^{j - 1},i+2^j-1]\)两部分

对应的是\(st[i][j - 1]\)和\(st[i + (1 << j) - 1][j - 1]\)

\[st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]); \]

查询

\(O(1)\)

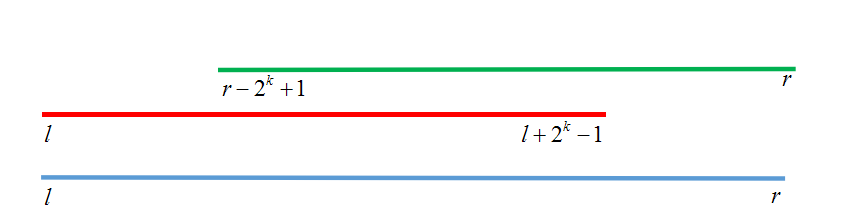
把\([l,r]\)分成两个有交集的区间\([l,l + 2^k-1]\)和\([r - 2^k + 1][r]\)

\[k = log2(r - l + 1)\\ ans = max(st[l][k],st[r - (1 << k) + 1][k]) \]

打表观察

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const int N = 3e5 + 5;
int st[N][22];
int main(){
    int n = 20;
    for(int j = 1; j <= 20; j++)
        for(int i = 1; i + (1 << j) - 1 <= n; i++)
            printf("%d [%d,%d] [%d,%d]\n", 1 << (j - 1), i, i + (1 << (j - 1)) - 1, i + (1 << (j - 1)), i + (1 << j) - 1);
    return 0;
}

{{uploading-image-762726.png(uploading...)}}

可以观察其变化情况

模板

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const int N = 1e5 + 5;
int st[N][20];
int query(int l, int r){
    int k = log2(r - l + 1);
    return max(st[l][k], st[r - (1 << k) + 1][k]);
}
int main(){
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
        scanf("%d", &st[i][0]);
    
  int k = log2(n / 2) + 1; //常数优化
    for(int j = 1; j <= 17; j++) // j in [1, k]
        for(int i = 1; i +(1 << j) - 1 <= N; i++)
            st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
    for(int i = 1; i <= m; i++){
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", query(l, r));
    }
    return 0;
}

扩展

st表必定是一个单调函数

• 维护最大值的st表 - 单调递增
• 维护最小值的st表 - 单调递减

可以用二分去寻找满足条件的区间个数

遍历下左区间，然后二分在st表里查找右区间

同时，st表也可以去维护其他的，比如区间LCA

总之，对于区间RMQ问题，或者区间问题，多组查询，且不修改，ST表很好用