结对编程作业

结对队友博客地址：https://www.cnblogs.com/minskiter/p/13816780.html
自己博客地址： https://www.cnblogs.com/ElizzF/p/13780877.html
张郑峰微信小程序+原型html+游戏视频演示Github项目地址：https://github.com/ElizzF/Picture-Klotski
后端Github项目地址： https://github.com/minskiter/klotski.git
具体分工：

姓名	工作	github	github内容
张郑峰	微信小程序开发，与后端交互，做原型	Elizzf	微信小程序，原型设计，游戏演示视频
叶飞扬	后端微服务开发，AI大比拼对接，微信小程序前后端对接	Minskiter	AI程序(klotskiserver)，图片处理程序（graph-python),AI大比拼简陋界面(apirank)

1、原型设计

1.1、设计说明

=
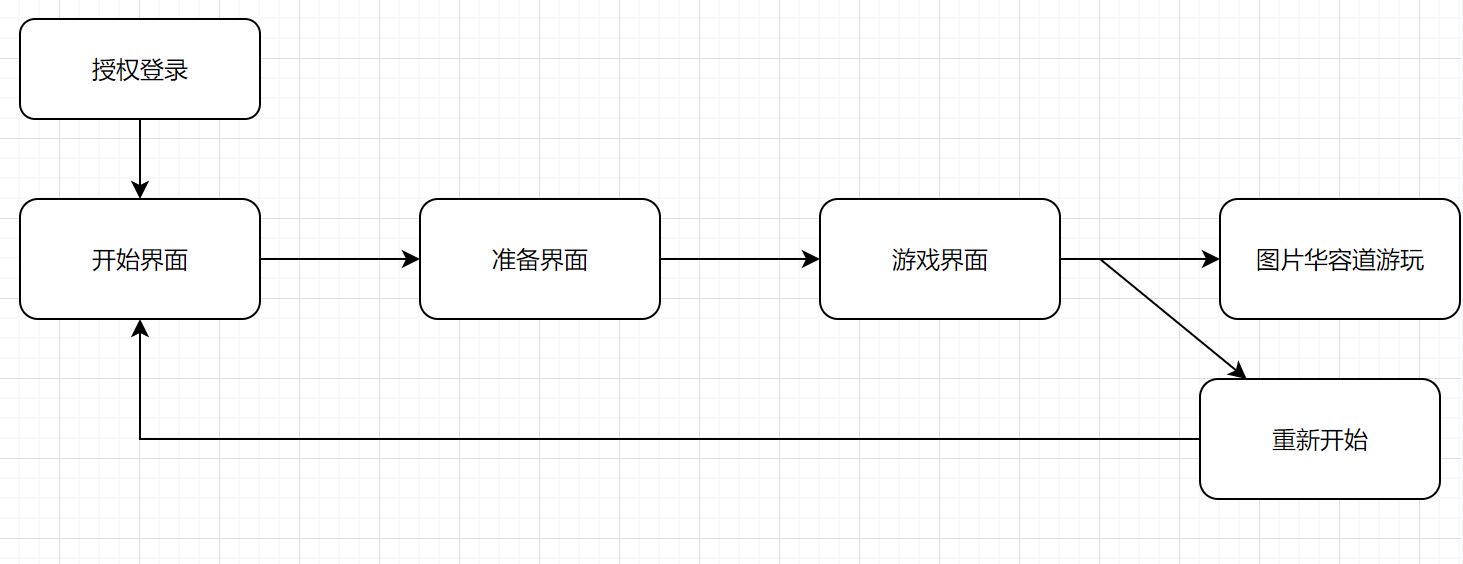
整体页面结构如下：
因为是做游戏，因此结构并没有太过复杂，一个开始界面，一个准备界面（用来预览要实现的目标图片），一个游戏界面，其中开始界面和游戏界面有弹窗事件。

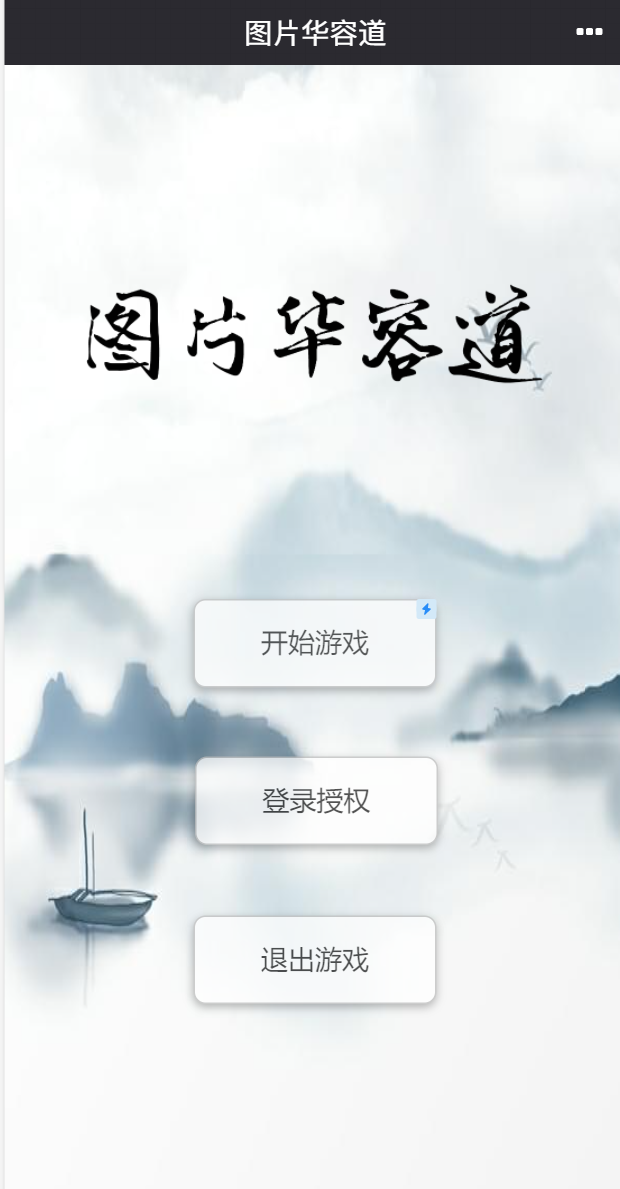
首先，开始界面，点击开始游戏进入准备界面，但是在进入前要进行登录授权，否则拒绝用户开始游戏。
登录授权用途是用来保存每个玩家的历史记录（历史最短步数/历史最快时间），点击后会弹窗提示可以开始游戏。
退出游戏顾名思义。

然后是准备界面
这里显示游戏规则以及将要拼接的游戏的目标图案，玩家需要记住这个图案，因为在正式游戏界面我们并不会再给予玩家观看的机会（考验玩家记忆力）。

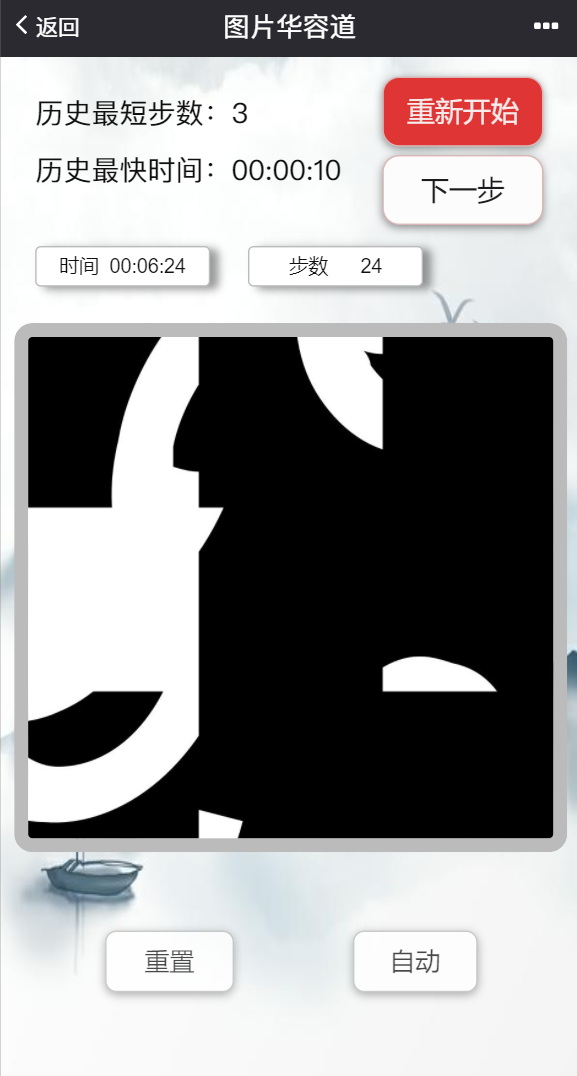
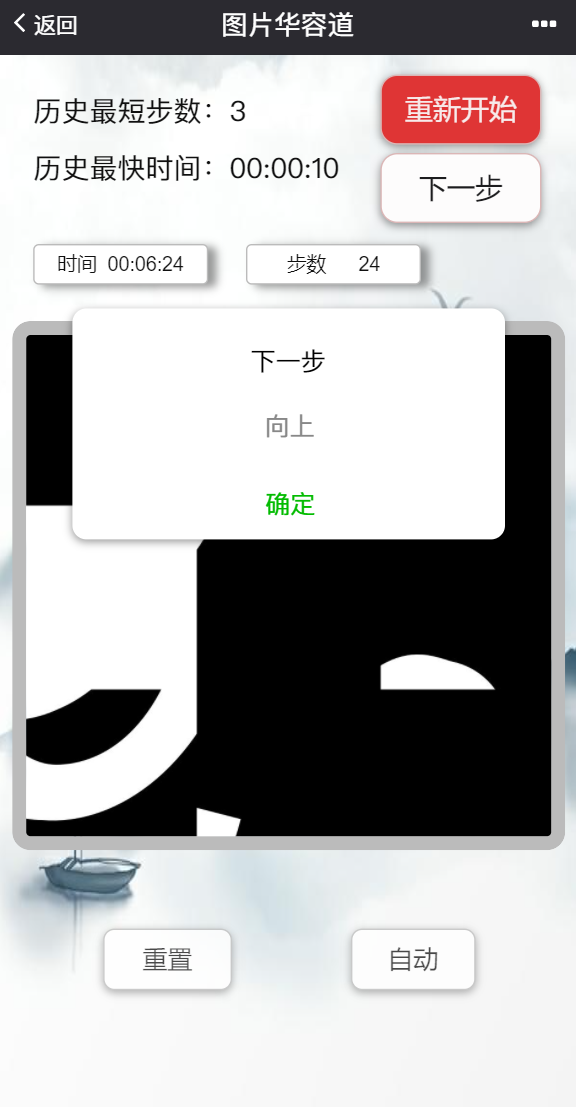
游戏界面
大致有下面几个功能：
1）游戏。玩家点击空白格附近的图片格，图片格将与空白格交换，步数+1，另外有计时。目标即为将打乱的图片格最终变换为准备界面中目标图案缺一格的情况。
2）重新开始。点击后玩家将返回开始界面，此时再次点击开始游戏，将会随机替换成其它图案。
3）重置。玩家点击后图案将会回到刚开始游戏的时候的样子，步数清0，但计时仍继续。
4）自动。玩家点击后，图案将会按照内嵌的AI一步步自动复原，但此时游戏结束并不会将步数和时间记录在历史记录中（因为不是玩家手动的）
5）下一步。点击后，会提示玩家下一步往哪走（路径与AI自动一致）。
6）历史记录。玩家每次成功复原图案后，所消耗步数和时间将会记录下来，其中最短步数和最快时间会显示给玩家看，让玩家突破自我.gif。

1.2、使用的原型工具： 墨刀

1.3、结对的过程

讨论原型设计图片

1.4、遇到的困难及解决方法:

困难描述
一开始不懂图片华容道要怎么玩。
原型工具刚开始用很多功能不懂怎么使用。
解决尝试
按作业上所述找了数字华容道来玩就明白怎么玩了。
原型工具方面本来想自己慢慢摸索，但最终还是面向百度。
是否解决
上述困难都解决了。
有何收获
玩到了一个以前没玩过的游戏
以前看产品做过原型但没尝试过，这次亲身体会了一次，明白怎么做原型了。

2、AI与原型设计实现

2.1、代码实现思路

网络接口的使用

服务对外提供http1.1 restful web api以支持小程序端对端调用，内部使用grpc http2.0远程调用实现dotnet core调用python函数。

代码组织与内部实现设计（类图）

以下是控制层和服务层以及部分帮助API的类图，隐藏了Model层的数据类（即不在图中）

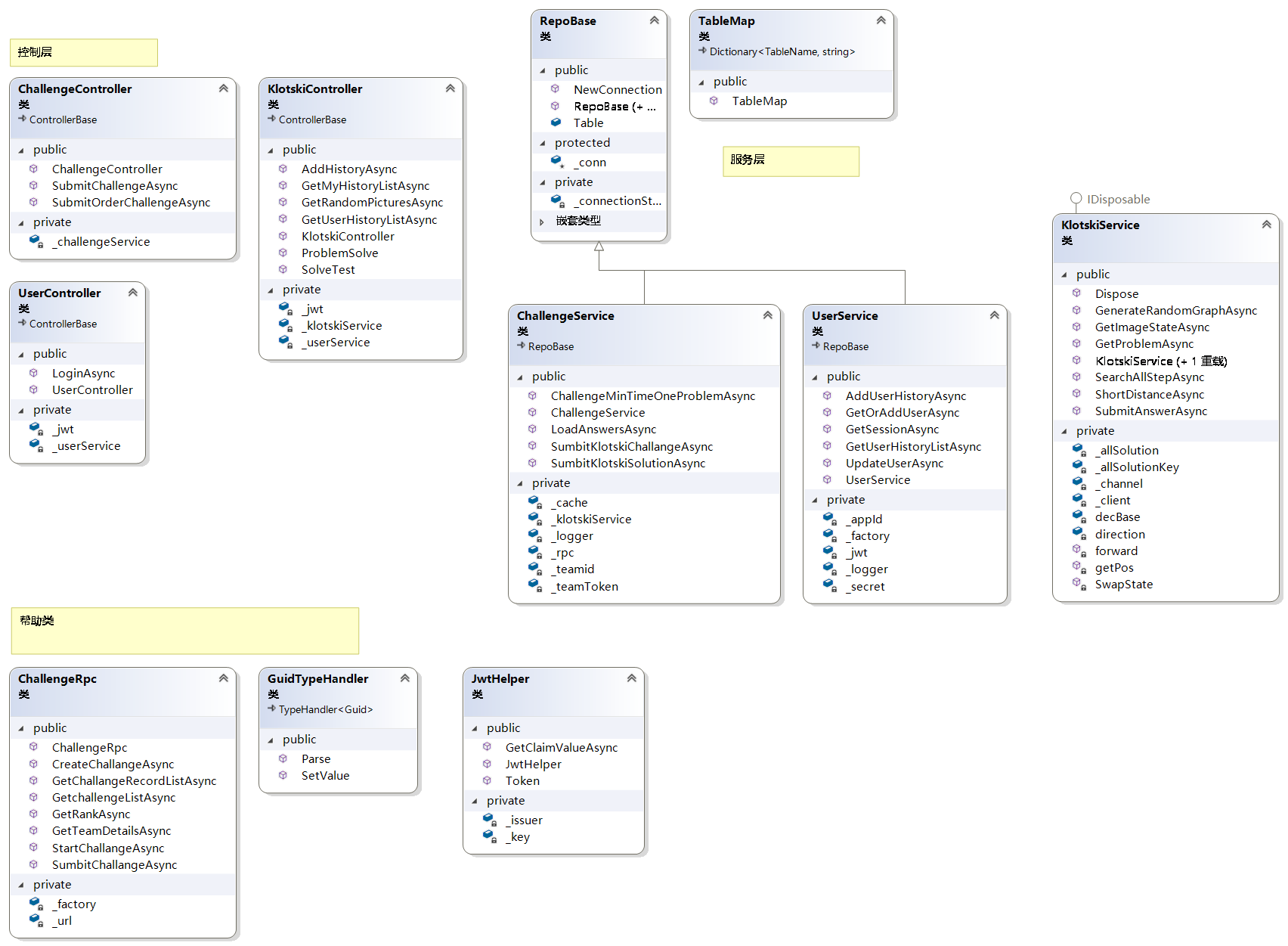
代码基于MVC分层设计思想，由于没有View层，因此层次主要是Controller层、Service层（直接包含CRUD操作）以及Model

python端

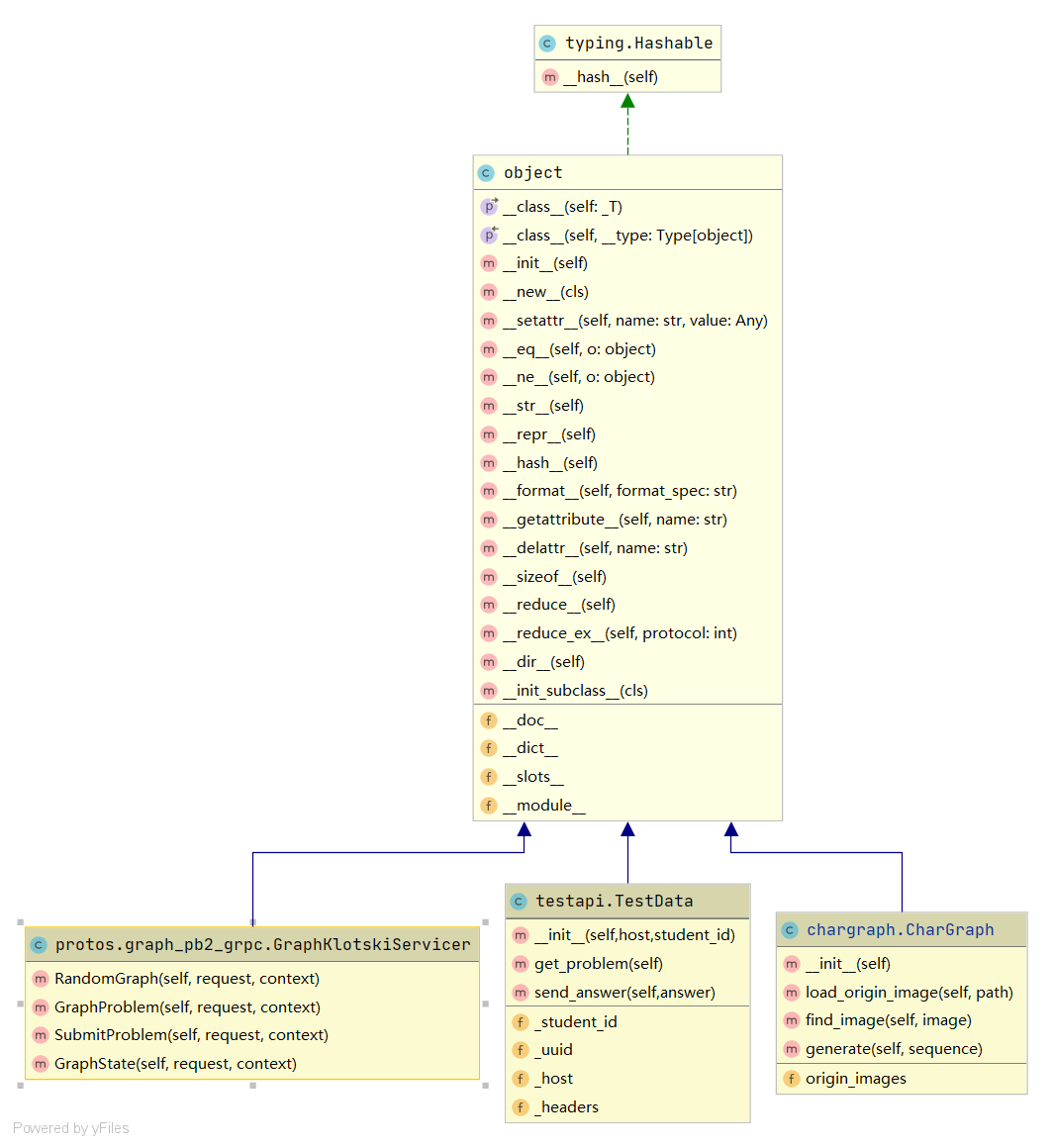
Testapi负责前期的基础测试
CharGraph负责图像的匹配以及处理，通过预加载所有图片到内存中，并计算其特征值，利用特征值达到快速匹配

说明算法的关键与关键实现部分流程图

AI首先想到的是搜索，搜索有两种，深度优先搜索以及广度优先搜索以及两种结合起来利用评估函数来进行预测的启发式搜索。综合考虑时间以及步数最优的情况采用广度优先搜索（由后面步数产生并不会影响到之前的状态可简单的推出动态规划是可行的，动态规划也是最差的A*算法，因此可以求出最低解），因此采用广度优先搜索+记录最小步数的状态。而路径即回溯寻找父节点即可。同时，在时间方面上，所有的状态仅有9!/2*9(大概162万种有解状态）左右，可以直接缓存在内存中，加速搜索速度，同时判断有无解也可以在o(1)的时间内得出结果。
图片判断是否python来判断以支持跨平台部署。
算法大致流程图如下所示：

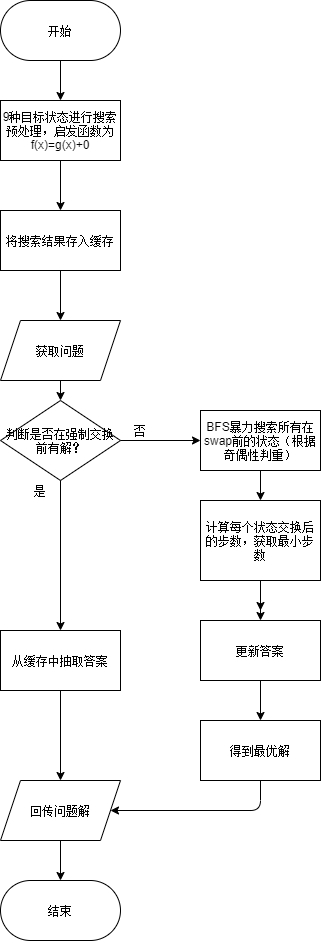
贴出你认为重要的/有价值的代码片段，并解释

图片匹配采用简单的缩放以及硬匹配，当然该匹配还有很大的优化空间例如匹配两次后不需要再进行匹配，以及hash全局粗筛再进行细匹配

def find_image(self,image):
        ''' 
            匹配图片

            Attributes:
                image: numpy, numpy图像数组

            Returns:
                ans: [{'dest':0,'origin':2},...]  目标位置，图片所在位置
        '''
        spilt_images = []
        rows = np.split(image,3,axis=0)
        for row in rows:
            cols = np.split(row,3,axis=1)
            for col in cols:
                spilt_images.append({
                    'image':col,
                    'hash':Image.fromarray(col).resize((8,8)).tobytes()
                })
        ans=None
        for originImage in self.origin_images:
            matches = 0
            matches_array = []
            for origin_index,origin_split in enumerate(originImage['images']):
                exists = {} # 去重
                for split_index,split_image in enumerate(spilt_images):
                    if origin_split['hash']==split_image['hash'] and split_index not in exists:
                        matches_array.append({
                            'dest':origin_index,
                            'origin':split_index
                        })
                        exists[split_index]=True
                        matches+=1
                        break
            if matches>=8:
                ans=matches_array
                return ans
        return ans

算法部分采用双向广搜，详细见上图算法流程图

        /// <summary>
        /// 初始化所有可能的情况
        /// </summary>
        /// <returns></returns>
        public async Task<Dictionary<long, KlotStep>> SearchAllStepAsync()
        {
            return await Task.Run(() =>
            {
                // 初始化初始节点状态
                // 9代表空格，0，1，2，3，4，5，6，7，8代表格子的原始位置
                // 初始状态总共有9种，从9种广搜获取所有状态的最短路径
                var initState = new long[]{
                976543210,
                896543210,
                879543210,
                876943210,
                876593210,
                876549210,
                876543910,
                876543290,
                876543219,
            };
                var visited = new Dictionary<long, KlotStep>();
                var searchQuery = new Queue<long>();
                var index = 0;
                foreach (var state in initState)
                {
                    searchQuery.Enqueue(state);
                    visited.Add(state, new KlotStep
                    {
                        step = 0,
                        father = -1,
                        blankPos = 8 - index
                    });
                    ++index;
                };
                while (searchQuery.Count > 0)
                {
                    var state = searchQuery.Dequeue(); // 出队，获取状态
                    var lastStep = visited[state];
                    foreach (var dir in direction)
                    {
                        int nextPos = lastStep.blankPos + dir;
                        if (nextPos % 3 == 0 && dir == 1) continue;
                        if (nextPos % 3 == 2 && dir == -1) continue;
                        if (nextPos < 0 || nextPos > 8) continue;
                        var nextState = SwapState(lastStep.blankPos, nextPos, state);
                        if (visited.ContainsKey(nextState)) continue;
                        var currentStep = new KlotStep
                        {
                            father = state,
                            blankPos = nextPos,
                            step = lastStep.step + 1
                        };
                        visited.Add(nextState, currentStep);
                        searchQuery.Enqueue(nextState);
                    }
                }
                return visited;
            });
        }

        /// <summary>
        /// 最短路径解
        /// </summary>
        /// <param name="state">华容道的状态</param>
        /// <param name="step">步数</param>
        /// <param name="swap">交换的位置</param>
        /// <returns></returns>
        public async Task<KlotOperations> ShortDistanceAsync(long state, int step, List<int> swap)
        {
            return await Task.Run(() =>
            {
                step = step + 1;
                // 查看是否当前状态可在交换前出结果
                var launchStep = _allSolution;
                var operations = new KlotOperations();
                if (launchStep.TryGetValue(state, out var path))
                {
                    if (path.step < step)
                    { // 参考设定为step是从1开始计算的，1算第一步，这里path的step从1开始计算
                        while (path.father != -1)
                        {
                            char forw = forward(path.blankPos, state, path.father);
                            operations.operations += forw;
                            state = path.father;
                            path = launchStep[path.father];
                        }
                        return operations;
                    }
                }
                var swapBeforeList = new List<long>(); // 交换前最后的状态
                var visited = new Dictionary<long, KlotStep>();
                // 这里的visited也包含记录步数信息
                var searchQuery = new Queue<long>();
                // 该状态state末尾代表奇偶次1代表奇数次，0代表偶数次
                searchQuery.Enqueue(state * 10);
                visited.Add(state * 10, new KlotStep
                {
                    step = 0,
                    father = -1,
                    blankPos = getPos(state)
                });
                while (searchQuery.Count > 0)
                {
                    // 这里的state包含奇偶次信息
                    state = searchQuery.Dequeue();
                    var lastStep = visited[state];
                    if ((step - 1 - lastStep.step) % 2 == 0)
                    { // 如果到强制交换前相差为偶数次，则可以通过反复横跳来到达目的 qwq
                        swapBeforeList.Add(state); 
                    }
                    if (lastStep.step == step - 1)
                    {
                        // swapBeforeList.Add(state);
                        continue;
                    } // 限制不能超过强制交换的步数
                    foreach (var dir in direction)
                    {
                        var nextPos = lastStep.blankPos + dir;
                        if (nextPos % 3 == 0 && dir == 1) continue;
                        if (nextPos % 3 == 2 && dir == -1) continue;
                        if (nextPos < 0 || nextPos > 8) continue;
                        var nextState = SwapState(lastStep.blankPos, nextPos, state / 10) * 10 + (lastStep.step + 1) % 2;
                        if (visited.ContainsKey(nextState)) continue;
                        var currentStep = new KlotStep
                        {
                            father = state,
                            blankPos = nextPos,
                            step = lastStep.step + 1
                        };
                        visited.Add(nextState, currentStep);
                        searchQuery.Enqueue(nextState);
                    }
                }
                // 全部搜索完毕，判断强制交换后是否有解决方案
                int minStep = -1;
                long solutionState = -1;
                var freeSwap = new List<int>();

                foreach (var beforeState in swapBeforeList)
                {
                    var nextState = SwapState(swap[0], swap[1], beforeState / 10);
                    if (launchStep.TryGetValue(nextState, out path))
                    {
                        if (minStep == -1 || path.step < minStep)
                        {
                            minStep = path.step;
                            solutionState = beforeState;
                            freeSwap.Clear();
                        }
                    }
                    else // 判断自由交换
                    {
                        var temp = nextState;
                        for (var i = 0; i < 9; ++i)
                        {
                            for (var j = 0; j < 9; ++j)
                            {
                                if (i != j)
                                {
                                    nextState = SwapState(i, j, temp);
                                    if (launchStep.TryGetValue(nextState, out path))
                                    {
                                        if (minStep == -1 || path.step < minStep)
                                        {
                                            minStep = path.step;
                                            solutionState = beforeState;
                                            freeSwap.Clear();
                                            freeSwap.AddRange(new int[] { i, j });
                                        }
                                    }
                                }
                            }
                        }
                    }
                }
                // if (minStep == -1)
                // { // 无解的情况，则自由变换任意格子,交换后必定存在至少一个解
                //     foreach (var beforeState in swapBeforeList)
                //     {
                //         var nextState = SwapState(swap[0], swap[1], beforeState/1000);
                //         var temp = nextState;
                //         for (var i = 0; i < 9; ++i)
                //         {
                //             for (var j = 0; j < 9; ++j)
                //             {
                //                 if (i != j)
                //                 {
                //                     nextState = SwapState(i, j, temp);
                //                     if (launchStep.TryGetValue(nextState, out path))
                //                     {
                //                         if (minStep == -1 || path.step < minStep)
                //                         {
                //                             minStep = path.step;
                //                             solutionState = beforeState;
                //                             freeSwap.Clear();
                //                             freeSwap.AddRange(new int[] { i, j });
                //                         }
                //                     }
                //                 }
                //             }
                //         }
                //     }
                // }
                long swapAfterState = SwapState(swap[0], swap[1], solutionState / 10);
                // 这里的swapAfterState 不包括奇偶次信息
                if (freeSwap.Count > 0)
                {
                    swapAfterState = SwapState(freeSwap[0], freeSwap[1], swapAfterState);
                    operations.swap = freeSwap;
                }
                // 生成路径解
                path = visited[solutionState];
                if (path.step != step - 1)
                {
                    // 计算反复横跳的次数 qwq
                    for (var i = 0; i < step - 1 - path.step; ++i)
                    {
                        if (i % 2 == 0)
                        {
                            // operations.operations = forward(fatherPos, path.father, swapBeforeState) + operations.operations;
                            if (path.blankPos % 3 == 0) operations.operations = 'a' + operations.operations;
                            else operations.operations = 'd' + operations.operations;
                        }
                        else
                        {
                            // operations.operations = forward(path.blankPos, swapBeforeState, path.father) + operations.operations;
                            if (path.blankPos % 3 == 0) operations.operations = 'd' + operations.operations;
                            else operations.operations = 'a' + operations.operations;
                        }
                    }

                }
                // 计算横跳之前的步数
                while (path.father != -1)
                {
                    var fatherPos = getPos(path.father / 10);
                    operations.operations = forward(fatherPos, path.father / 10, solutionState / 10) + operations.operations;
                    solutionState = path.father;
                    path = visited[path.father];
                }

                // 计算交换后的步数
                path = launchStep[swapAfterState];
                // 此处为测试判断的一个小bug，需要额外添加一步以触发强制交换
                // if (path.father == -1)
                // {
                //     if (path.blankPos % 3 == 0)
                //     {
                //         operations.operations += 'd';
                //     }
                //     else
                //     {
                //         operations.operations += 'a';
                //     }
                // }
                while (path.father != -1)
                {
                    operations.operations += forward(path.blankPos, swapAfterState, path.father);
                    swapAfterState = path.father;
                    path = launchStep[path.father];
                }
                if (operations.swap.Count > 0)
                {
                    for (var index = 0; index < operations.swap.Count; ++index)
                    {
                        operations.swap[index]++;
                    }
                }
                return operations;
            });

原本情况是没有奇数情况的，但是因为在AI大比拼测试的时候偶然发现步数会更少（后来猜测可能是评测错误？现在实测步数并没有减少）

性能分析与改进

在优化上首先是缓存优化，对于双向广搜来说，目标9个节点是已知的，从9个节点反向搜索产生的162w情况可以直接缓冲到内存里以供程序快速调用；（没有缓冲时，测试的平均时间为1.4s左右，当加入缓存后，时间可以进一步缩减到0.25s左右，当然空间使用多了100MB，相当于空间换时间吧）
对于API大比拼特别优化答案缓存，以方便二刷后直接有效降低时间（在由于后期缓存过多，采用字符串hash效率低，导致末尾的二刷并没有减少时间）

描述你改进的思路

python处理循环效率相对来说比较差，与c，c#，java之类对比同类的函数可能多了常数倍的时间，因此可使用c语言进行转译以加快速度；
图片匹配使用的是暴力循环，可加上hash全局定位以及部分匹配剪枝优化。

展示性能分析图和程序中消耗最大的函数

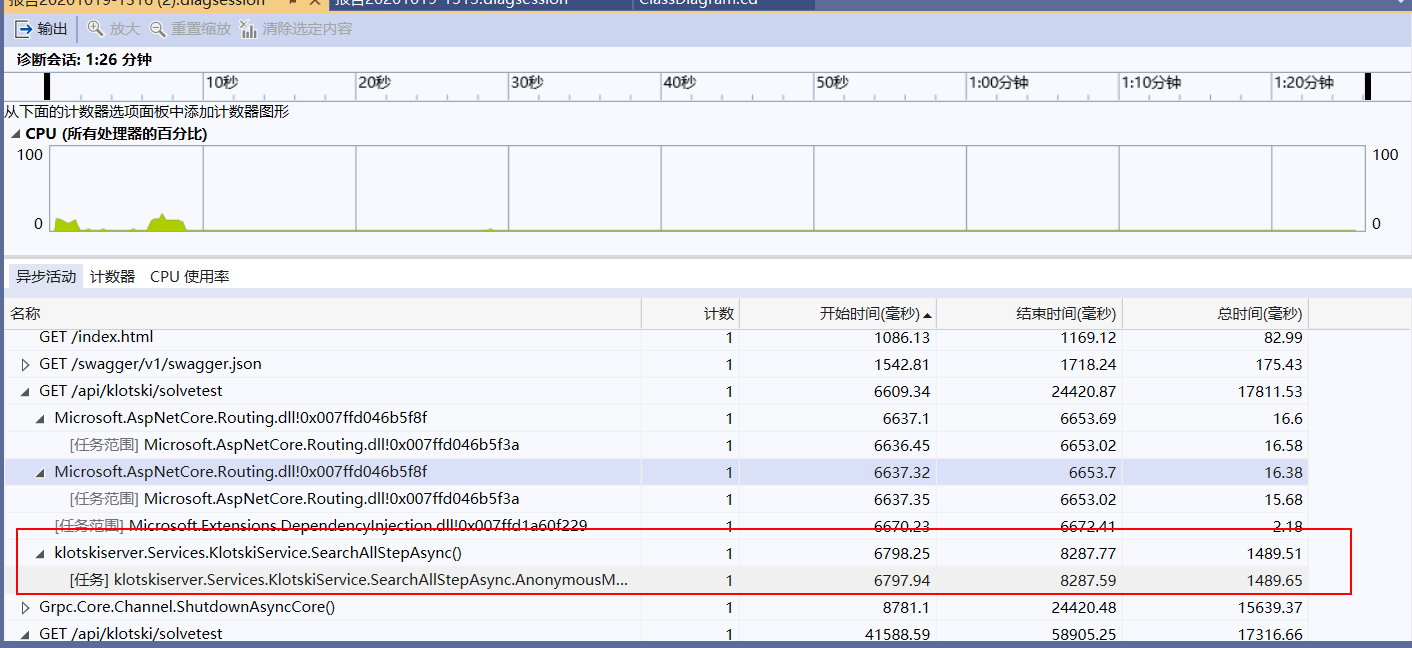
由图示可见消耗最多的是1.4s的预处理搜索，但是改部分除了首次加载以外，之后皆由缓存中获取，可见缩减到了1.54ms

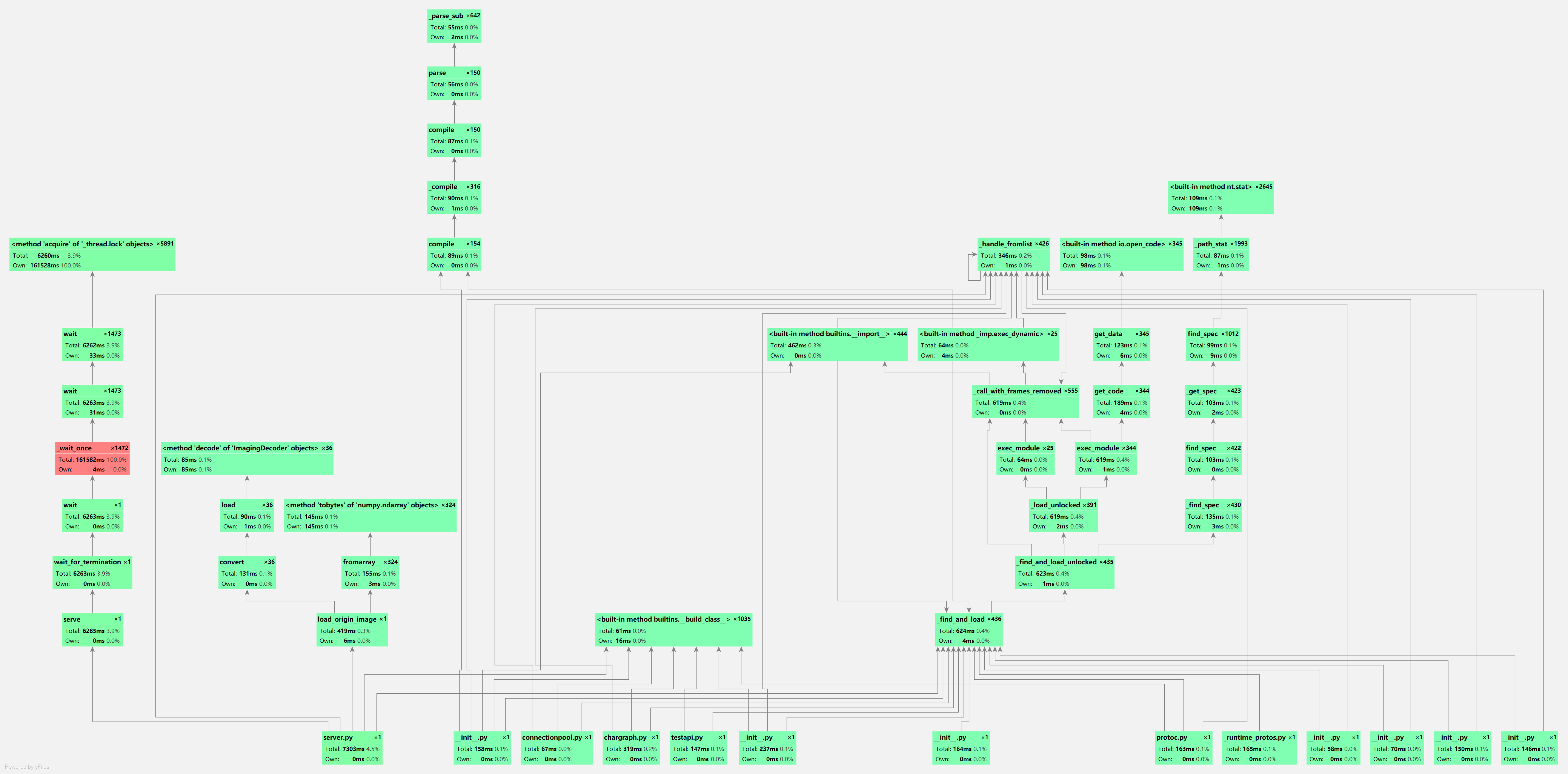
python主要的消耗在于启动服务以及加载图片，但由于这些都是预处理程序，并不影响后面的快速匹配

展示出项目部分单元测试代码，并说明测试的函数，构造测试数据的思路

测试目前是采用接口级别的测试，由于源代码使用了依赖注入，单元测试需要使用mock模拟类实现单元测试，故本次只是基于网络的API层面上的测试。

import requests
import json
import time
import math

success_count = 0
calc_time = 0
max_time = 0

for i in range(1,200):
    res = json.loads(requests.get("http://localhost:5000/api/klotski/solvetest").text)
    if not res['score']['score']:
        print(res)
    else:
        calc_time += res['score']['time']
        max_time = max(res['score']['time'],max_time)
        success_count+=1
    if success_count>0:
        print("\r目前成功次数:{0} 平均时间用时{1}s 最长用时:{2}s".format(success_count,calc_time/success_count,max_time),end='')
    time.sleep(1)

2.2、贴出Github的代码签入记录，合理记录commit信息

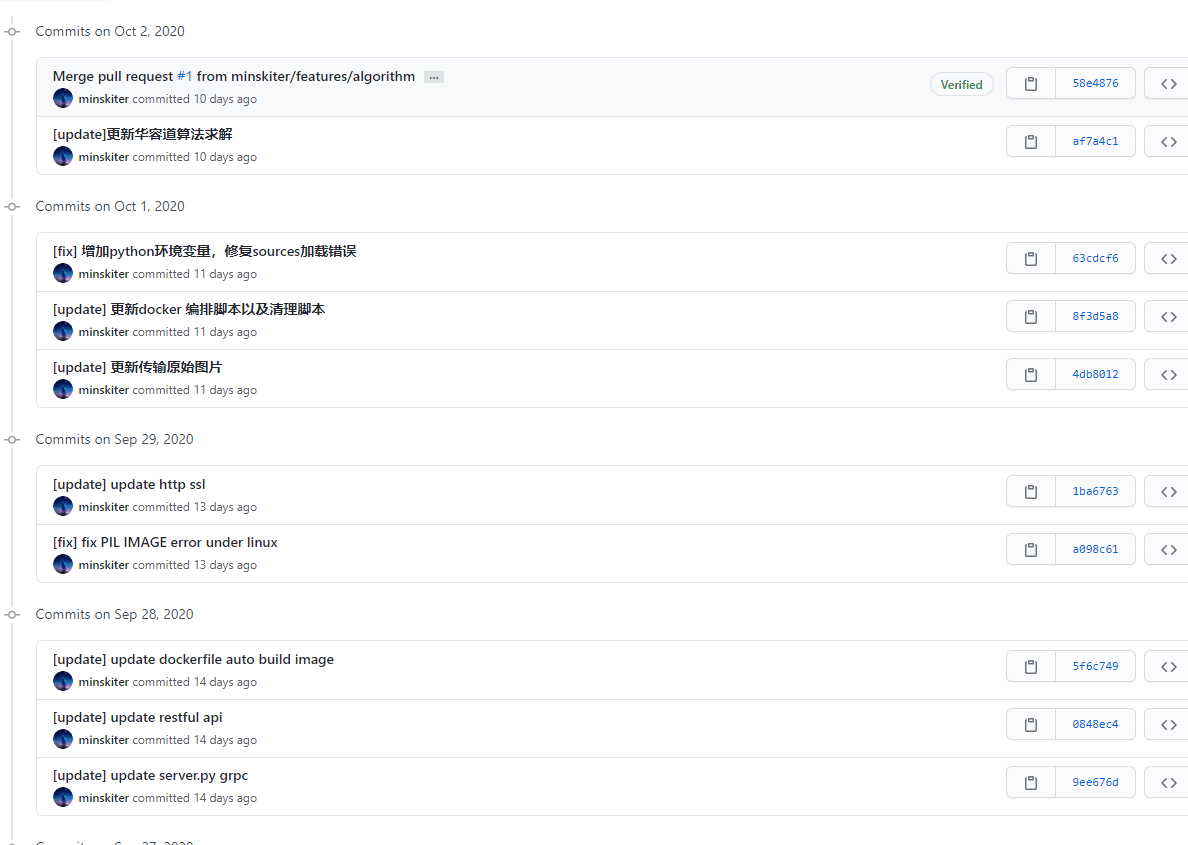
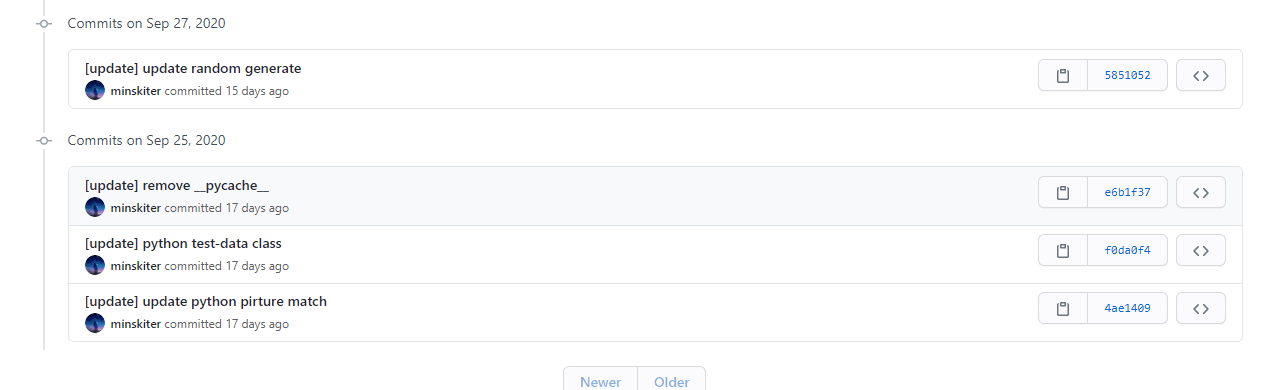
2.3、遇到的代码模块异常或结对困难及解决方法

困难描述
1、调试的时候由于图片顺序问题导致给出的解在提交到测试服务器上为无解状态，而手工模拟几次后无法解决错误；
2、强制交换时接着自由交换直接得出最终状态提交后为False
3、大比拼中出现了解不是最优的情况

解决尝试
人工模拟解法以及寻求测试组大佬的帮助，在大佬的帮助下，全部都解决了。最后一点是由于题目理解错导致判断无解为初始状态可达的所有状态无解。
是否解决
是
有何收获
修改bug唯有耐心+细心

2.4、评价你的队友

叶飞扬：

• 值得学习的地方：
  大佬效率很高，在第一周就完成了原型设计以及部分前端代码的编写，第二周就基本完成了前端代码。同时经常会主动进行交流，我应该向他学习，感觉自己的效率也跟着得到了巨大提升了QWQ。
• 需要改进的地方：
  大佬各方面都很好，很赞qwq。

张郑峰：

• 值得学习的地方：
  大佬会的技术非常多，全方面多方位发展，应该向他学习，另外做起事来非常有效率，接口在提出要求后很快就实现了。
• 需要改进的地方：
  我觉得已经很好了，没啥需要改进的了。

2.5、PSP和学习进度条

PSP表格

• 张郑峰：

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	60	60
· Estimate	· 估计这个任务需要多少时间	60	60
Development	开发	700	650
· Analysis	· 需求分析 (包括学习新技术)	150	160
· Design Spec	· 生成设计文档	60	60
· Design Review	· 设计复审	20	30
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	20	20
· Design	· 具体设计	60	50
· Coding	· 具体编码	360	300
· Code Review	· 代码复审	10	10
· Test	· 测试（自我测试，修改代码，提交修改）	20	20
Reporting	报告	60	60
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	20	20
	· 合计	820	770

• 叶飞扬：

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	60	60
· Estimate	· 估计这个任务需要多少时间	60	60
Development	开发	1500	1455
· Analysis	· 需求分析 (包括学习新技术)	60	360
· Design Spec	· 生成设计文档	60	60
· Design Review	· 设计复审	20	20
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30	10
· Design	· 具体设计	45	45
· Coding	· 具体编码	300	800
· Code Review	· 代码复审	15	60
· Test	· 测试（自我测试，修改代码，提交修改）	30	100
Reporting	报告	80	70
· Test Report	· 测试报告	40	30
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	30
	· 合计	1640	1585

学习进度条

• 张郑峰：

第N周	新增代码（行）	累计代码（行）	本周学习耗时（小时）	累计学习耗时（小时）	重要成长
1	100	100	8	8	上手了原型工具墨刀，了解如何进行原型设计，实现少部分页面
2	200	300	20	20	阅读微信小程序文档，将原型其余页面在微信小程序上实现
3	600	900	45	65	在微信小程序上进行前后端交互，初步实现在微信小程序上玩华容道
4	200	1100	12	77	原来基础上增添几个小功能，并对之前代码进行些许改进

• 叶飞扬：

第N周	新增代码（行）	累计代码（行）	本周学习耗时（小时）	累计学习耗时（小时）	重要成长
1	0	0	10	10	学习了华容道的一些特性，同时了解启发式搜索
2	650	650	12	22	实现了python端与dotnet端对接，同时进行了docker部署集成
3	560	1210	10	32	初步预设实现API大比拼对接，同时不断优化代码，对自动化构建脚本进行改进
4	200	1410	8	40	学习现有的其他算法，并对之前的代码进行改进优化

2.6、原型设计实现演示：

移动算法：代码中no = 9即空白块。

let index = e.currentTarget.dataset.index;
let numData = this.data.pictureData;
let step = this.data.step;
for (let i in numData) {
    if (index == i && numData[index].no != 9) {
    let x = '';
    // 当前点击的 上下左右 方向如果有空位的话，就互换位置
    if (numData[index - 3] && numData[index - 3].no == 9) {  // 下
        x = index - 3;
    } else if (numData[index + 3] && numData[index + 3].no == 9) {  // 上
        x = index + 3;
    } else if (numData[index - 1] && numData[index - 1].no == 9) {  // 左
        // 如果是在最左边的话，禁止向左移动
        for (let h = 1; h < 3; h++) {
        if (index == 3 * h) return;
        }
        x = index - 1;
    } else if (numData[index + 1] && numData[index + 1].no == 9) {  // 右
        // 如果是在最右边的话，禁止向右移动
        for (let h = 1; h < 3; h++) {
        if (index == 3 * h - 1) return;
        }
        x = index + 1;
    } else {
        return; // 没有空位不做任何操作
    }

    [numData[i], numData[x]] = [numData[x], numData[i]];
    step++;
    break;
    }
}

github上的演示视频因为是在微信开发者工具上运行，所以“自动”功能会卡顿直到一瞬间结束，而下方演示视频直接在微信小程序上演示，不会出现这种情况。
通过原型设计出的微信小程序视频演示