强连通分量
强连通分量
目录
-
基本概念
-
\(Kosaraju\)算法
-
\(Tarjan\)算法
-
例题讲解
-
题目推荐
-
学习资源
基本概念
- 连通图
在无向图中,从任意点\(i\)可以到达任意点\(j\)
- 强连通图
在有向图中,从任意点\(i\)可以到达任意点\(j\)
- 弱连通图(了解即可)
人为地将有向图看做无向图后,从任意点\(i\)可以到达任意点\(j\)
- 极大强连通子图
\(G\)是一个极大强连通子图,当且仅当\(G\)是一个强连通子图且不存在另一个强连通子图\(G'\),使得\(G\)是\(G'\)的真子集
- 强连通分量
有向非强连通图的极大强连通子图
因为来现实生活中有意义的强连通图很少,所以一般讨论的都是强连通分量
若将有向图中的强连通分量都缩为一个点,则原图就会变成一个DAG(有向无环图),如下图(1)-图(2)所示:
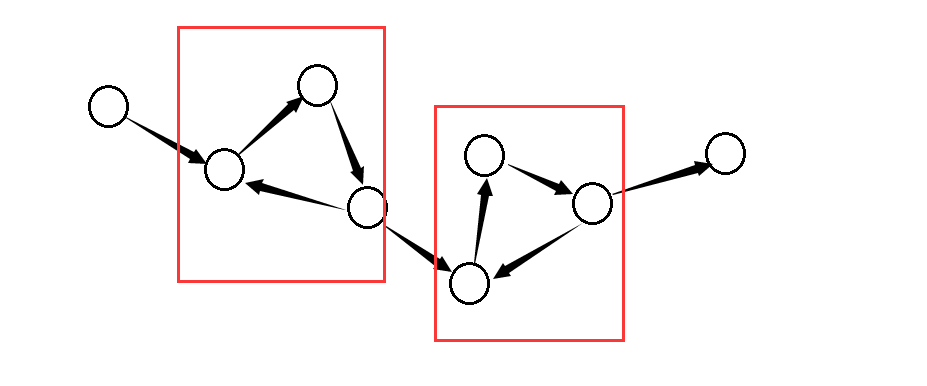 图(1)
图(1)
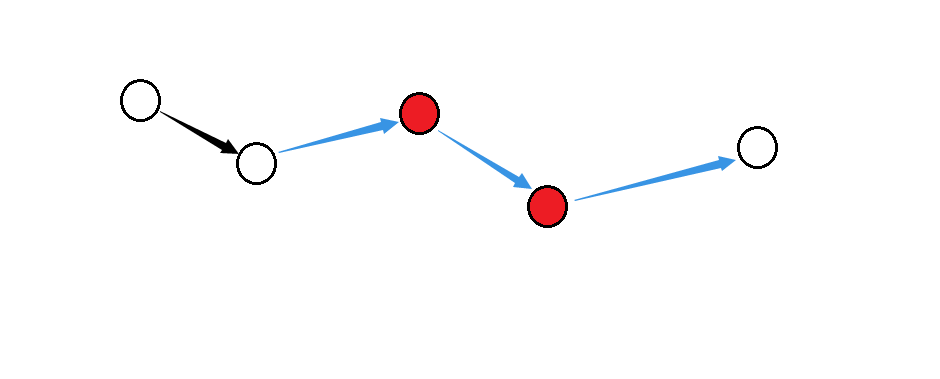 图(2)
图(2)
来讲(啰嗦 )一下,因为强连通分量相当于环啊,将环缩为点之后那就是无环图咯,这个很好想,证明的话反证法即可
- 强连通分量的应用
-
有向图的缩点:见上图示
-
解决\(2-SAT\)问题(还没学....之后更新啊qwq)
\(Kosaraju\)算法
基于两次\(DFS\)的有向图强连通分量算法,时间复杂度为\(O(n+m)\)
- 算法框架
-
对原图\(G\)进行\(DFS\),记录每个节点访问完的顺序\(dfn[i]\)并将点压入栈中
-
选择最晚访问完的节点对\(G\)的反向图进行第二次\(DFS\),删除能够遍历到的节点,每次遍历到的一坨(或一个)节点构成一个强连通分量
-
一直执行\((2)\)操作,直到所有节点都二次遍历完
- 例子图示

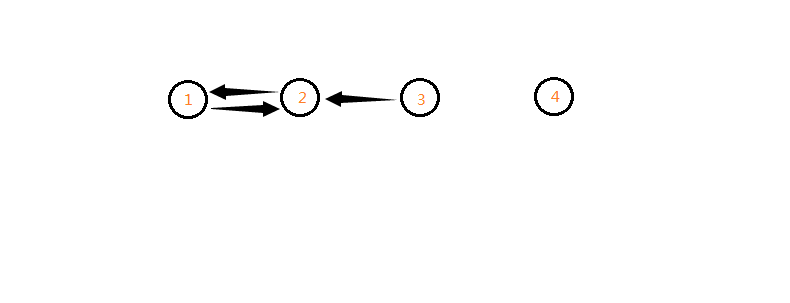
第一次\(DFS\)顺序:\(3->2->1->4\) (栈!)
第二次\(DFS\)顺序:\(4,2->1,3\) (一个逗号前为一个强连通分量)
- 代码函数段
个人认为比接下来的\(Tarjan\)好理解,但是使用的更多的还是扩展性更强的\(Tarjan\)
inline void dfs1(int x) {
vis[x]=1;
for(register int i=1;i<=n;i++) {
if(!vis[i]&&map[x][i]) dfs1(i);
dfn[++t]=x;
}
}
inline void dfs2(int x) {
vis[x]=t;
for(register int i=1;i<=n;i++) {
if(!vis[x]&&map[i][x]) dfs2(i);
}
}
inline void ko() {
t=0;
for(register int i=1;i<=n;i++) {
if(!vis[i]) dfs1(i);
}
memset(vis,0,sizeof(vis));
t=0;
for(register int i=n;i>=1;i--) {
if(!vis[dfn[i]]) {
t++;
dfs2(dfn[i]);
}
}
}
\(Tarjan\)算法
基于一次\(DFS\)的算法,时间复杂度也是\(O(n+m)\)
和\(kosaraju\)算法的\(DFS\)不同,\(Tarjan\)的\(DFS\)更类似于树的后序遍历
上图理解吧:
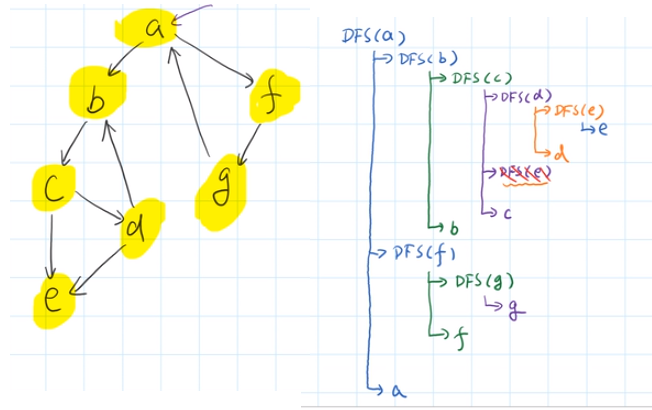
(图片截屏自我的学习视频,在文章最后会贴上,侵删!)
至于很多博客讲的四种边(树枝边、前向边、后向边、横叉边),我个人认为是没有必要掌握的,了解一下就可以了
- 所需变量
-
\(dfn[i]\):表示节点\(i\)的遍历顺序(同\(Kosaraju\)算法)
-
\(low[i]\):表示节点\(i\)可回溯到的最早遍历时间(初始与\(dfn[i]\)一致)
-
\(fir[i]=x\):表示节点\(i\)和节点\(x\)同属于一个强连通分量
-
\(q[top]\):手写栈qwq
5. 以及一啪啦的变量(可麻烦了)
- 算法框架
设当前点为\(x\)
-
初始\(dfn[x]\)=\(low[x]\)=\(++ti\)(时间戳)
-
入栈当前点并标记为访问过
-
遍历与\(x\)相连的点,进行下一层的\(DFS\),然后更新\(low[x]\)
-
遍历完后,如果当前\(x\)的\(dfn\)==\(low\),则可以弹出一个强连通分量了
可能有点抽象,如果不好理解,可以先跳到文末点击视频链接,里面讲得敲详细qwq
- 代码实现
以下代码是根据洛谷P3387 【模板】缩点 这道题编的,大家注意区分啊
另外,下面这份代码涉及到的拓扑排序,有兴趣的可以看我的另一篇博客
(PS:变量申请那块奇丑...轻喷)
#include <bits/stdc++.h>
using namespace std;
int n,m,u,v,tot,ans,a[520010],in[520010],fir[520010],head[520010];
int ti,top,num,q[520010],vis[520010],dis[520010],sum[520010],dfn[520010],low[520010];
struct node {
int to,net,fro;
} e[520010],es[520010];
inline void add(int u,int v) {
e[++tot].to=v;
e[tot].fro=u;
e[tot].net=head[u];
head[u]=tot;
}
inline void tarjan(int x) {
dfn[x]=low[x]=++ti;
q[++top]=x;
vis[x]=1;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(!dfn[v]) {
tarjan(v);
low[x]=min(low[x],low[v]);
}
else {
if(vis[v]) low[x]=min(low[x],dfn[v]);
}
}
if(low[x]==dfn[x]) {
int v=q[top];
while(top) {
fir[v]=x;
vis[v]=0;
if(v==x) {
top--;
break;
}
a[x]+=a[v];
v=q[--top];
}
}
}
inline void topo() { //拓扑排序求最长路
queue<int> q;
for(register int i=1;i<=n;i++) {
dis[i]=a[i];
if(!in[i]&&fir[i]==i) q.push(i);
}
while(!q.empty()) {
int x=q.front();
q.pop();
for(register int i=head[x];i;i=es[i].net) {
int v=es[i].to;
dis[v]=max(dis[v],dis[x]+a[v]);
if(--in[v]==0) q.push(v);
}
}
}
int main() {
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++) scanf("%d",&a[i]);
for(register int i=1;i<=m;i++) {
scanf("%d%d",&u,&v);
add(u,v);
}
for(register int i=1;i<=n;i++) {
if(!dfn[i]) tarjan(i);
}
tot=0;
memset(vis,0,sizeof(vis));
memset(head,0,sizeof(head));
for(register int i=1;i<=m;i++) {
u=fir[e[i].fro];
v=fir[e[i].to];
if(u!=v) {
in[v]++;
es[++tot].to=v;
es[tot].net=head[u];
es[tot].fro=u;
head[u]=tot;
}
}
topo();
for(register int i=1;i<=n;i++) ans=max(ans,dis[i]);
printf("%d",ans);
return 0;
}
例题讲解
洛谷P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G
个人认为很模板的题,思路稍微转换一下就出来了,写个小题解当做例题讲解qwq
- 分析
奶牛们之间的喜爱是单向的、可传递的,那么将文字描述抽象一下,即:
奶牛们是点,喜爱关系是单向边,整个关系则构成了有向图
相互喜爱的一群牛组成一个集合,则\(N\)头牛可以划分为\(S\)个集合(缩点的思想,缩环为点)
集合与集合之间也存在喜爱关系,则原图就转化为了DAG(有向无环图)
这个时候我们就需要思考一下:到底什么样的牛是所有牛喜欢的那个?
显然:是出度为\(0\)的集合中的牛
为什么?因为出度为\(0\)则说明这个集合不喜爱其他的牛,则满足所有牛都喜欢这头牛(有点绕,画一下图会好一点,作者懒不想画了QAQ)
由此,我们就将问题转换为了:缩点,然后求出度为\(0\)的点
现在给出以上思路的\(AC\)程序:
#include <bits/stdc++.h>
using namespace std;
int n,m,u,v,tot,num,out[520010],sum[520010],head[520010];
int ti,top,q[520010],val[520010],fir[520010],vis[520010],dfn[520010],low[520010];
struct node {
int to,net,fro;
} e[520010];
inline void add(int u,int v) {
e[++tot].to=v;
e[tot].fro=u;
e[tot].net=head[u];
head[u]=tot;
}
inline void tarjan(int x) {
dfn[x]=low[x]=++ti;
q[++top]=x;
vis[x]=1;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(!dfn[v]) {
tarjan(v);
low[x]=min(low[x],low[v]);
}
else {
if(vis[v]) low[x]=min(low[x],dfn[v]);
}
}
if(low[x]==dfn[x]) {
int v=q[top];
while(top) {
fir[v]=x;
vis[v]=0;
if(v==x) {
top--;
break;
}
val[x]+=val[v];
v=q[--top];
}
}
}
int main() {
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++) val[i]=1;
for(register int i=1;i<=m;i++) {
scanf("%d%d",&u,&v);
add(u,v);
}
for(register int i=1;i<=n;i++) {
if(!dfn[i]) tarjan(i);
}
for(register int i=1;i<=m;i++) {
u=fir[e[i].fro];
v=fir[e[i].to];
if(u!=v) out[u]++;
}
for(register int i=1;i<=n;i++) {
if(!out[i]&&fir[i]==i) {
sum[++num]=val[i];
}
}
if(num==1) printf("%d",sum[num]);
else if(num>=2) puts("0");
return 0;
}
PS:以下内容为我的无脑暴力骗分代码,可以跳过(52\(pts\)真香)
#include <bits/stdc++.h>
using namespace std;
int n,m,u,v,sum,flag;
int in[520010],out[520010];
int main() {
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++) {
scanf("%d%d",&u,&v);
out[u]++;
in[v]++;
}
for(register int i=1;i<=n;i++) {
if(out[i]==0) sum++;
}
if(sum==1) printf("1");
else if(sum>=2) printf("0");
else if(sum==0){
for(register int i=1;i<=n;i++) {
if(out[i]!=in[i]) {
flag=true;
break;
}
}
if(flag==false) printf("%d",n);
}
return 0;
}
例题讲解(正文)完毕~~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号