关于角平分线与抛物线

题设

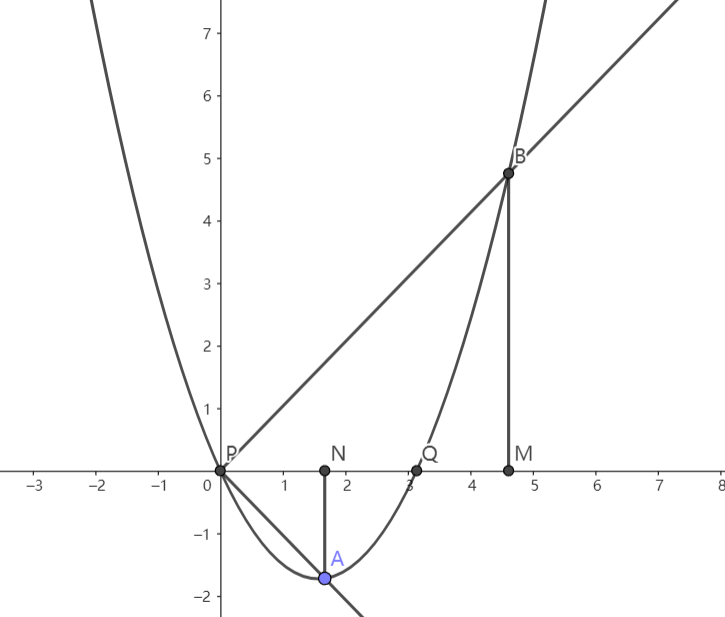
如图,设有一平面直角坐标系\(xOy\),有一抛物线\(y=k(x-x_1)(x-x_2)\),过\(P (x1,0)\)点引出两条直线交抛物线于\(A\),\(B\)

过\(A\)作$AN\perp x轴 $ , 过$ B $作 \(BM \perp x轴\) ,若 \(\angle APN=\angle BPM\),则\(NM\)中点为\(Q(x2,0)\)

证明

设\(A(a,k(a-x_1)(a-x_2)),B(b,k(b-x_1)(b-x_2))\)

\(AN=-k(a-x_1)(a-x_2),BM=k(b-x_1)(b-x_2),MP=a-x_1,NP=b-x_1\)

\(\tan \angle APN=\tan \angle BPM,\frac{AN}{PN}=\frac{BM}{PM}\)

\(-k(a-x_2)=k(b-x_2),a+b=2x_2,\) \(NM\)中点为\(Q\)

逆定理及证明

若得知\(Q\)为\(NM\)中点,回推\(\angle APN=\angle BPM\)

同理设\(A(a,k(a-x_1)(a-x_2)),B(b,k(b-x_1)(b-x_2))\)

因为\(NM\)中点为\(Q\),\(a+b=2x_2,-k(a-x_2)=k(b-x_2)\)

\(\frac{AN}{PN}=\frac{BM}{PM},\tan \angle APN=\tan \angle BPM\)

所以\(\angle APN=\angle BPM\)