一元三次方程的一般研究(1)

前言

众所周知,初中学子在做几何大题的时候经常会碰见一元三次方程.

所以本文会介绍几个初中范围内可行的一元三次方程解法.

猜根+长除法

具体解法

众所周知,\(26\),\(27\)题的数一般不会给的很恶心(大概),所以这个时候如果能大致猜出来形如\(ax^3+bx^2+cx+d\)的一个根为\(x_1=p\),而后通过长除法把原式子中\((x-p)\)除掉,之后就会得到一个二次方程

那么长除法是什么呢:

长除法

首先把被除式、除式按某个字母作降幂排列，缺项补零:

1.用分子的最高次项除以分母的最高次项，得到首商，写在横线之上。

2.将分母乘以首商，乘积写在分子前两项之下, 同类项对齐。

3.从分子的相应项中减去刚得到的乘积，得到第一余式，写在下面。然后，将分子的下一项“拿下来”。

4.把第一余式当作新的被除式，重复前三步，得到次商与第二余式（直到余式为零或余式的次数低于除式的次数时为止．\(被除式=除式\times 商式+余式\) ）。

5.重复第四步

举例:

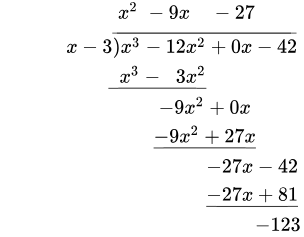
也就是说,\(\frac{x^3-12x^2-42}{x-3}=x^2-9x-27-\frac{123}{x-3}\)

算数长除法本质上是\(x=10\)的时候的长除法

例子

解方程\(2x^3−7x^2+7x−2=0\),通过代入观察不难发现一个根\(x_1=1\)

计算\(\frac{2x^3-7x^2+7x-2}{x-1}=x^2-\frac{5}{2}x+1=(x-2)(x-0.5)\)

\((x-1)(x-2)(x-0.5)=2x^3−7x^2+7x−2=0\)

\(x_1=1,x_2=2,x_3=0.5\)

本质是利用特殊方法进行因式分解

形如ax^3+bx+c=0的一元三次方程解法

我们知道猜根其实不容易,还需要拥有拉马努金级别的\(attention\),那么如何应对较为一般的一元三次方程呢,在介绍这个解法之前,需要一个前置知识

完全立方公式

\((m+n)^3=m^3+n^3+3mn(m+n)\)

也就是\((m+n)^3-m^3-n^3-3mn(m+n)=0.......(1)\)

推导方法不难理解,展开后再合并,读者可以尝试自证下面是证明

\((m+n)^3==m^3+n^3+3mn^2+3m^2n=m^3+n^3+3mn(m+n)\)

介绍具体解法

所以我们让等式两边除以\(a:x^3+\frac{b}{a}x+\frac{c}{a}=0......(2)\)

不难发现\((2)\)的式子与\((1)\)式很相似,也就是可以让\(-3mn=\frac{b}{a},-m^3-n^3=\frac{c}{a}\),列出下面方程

\(x^3-3mnx-m^3-n^3=0......(3)\)

使得\(x_1=m+n\)一定是原方程的一个解

接下来利用上面猜根后长除法的\(idea\),使得原式除以\((x-m-n)\)

得到\(x^2+(m+n)x+m^2+n^2-mn\),这里留给读者自证(其实是我不会画除法竖式的图)

即为\((3)\)等价于\((x-m-n)(x^2+(m+n)x+m^2+n^2-mn)=0\)

接下来根据二次方程的求根公式求出\(x^2+(m+n)x+m^2+n^2-mn=0\)的两个根,再加上\(x_1=(m+n)\)的一个根即可解决问题

接下来只有一点问题,怎么确定让\(-3mn=\frac{b}{a},-m^3-n^3=\frac{c}{a}的m,n的取值\)

\(m^3-n^3=\sqrt{(m^3+n^3)^2}=\sqrt{(m^3-n^3)^2-4m^3n^3}=\sqrt{(\frac{c}{a})^2-4{(\frac{b}{3a})}^2}.......(4)\)

再让\(-m^3-n^3=\frac{c}{a}与(4)相加\)

\(-2n^3=\sqrt{(\frac{c}{a})^2-4{(\frac{b}{3a})}^2}+\frac{c}{a}\)

\(n^3=-\frac{c}{2a}-\sqrt{(\frac{c}{2a})^2-{(\frac{b}{3a})}^2}\)

\(n=\sqrt[3]{-\frac{c}{2a}-\sqrt{(\frac{c}{2a})^2-{(\frac{b}{3a})}^2}}.......(5)\)

\((5)代入(4)得\)

\(m=\sqrt[3]{-\frac{c}{2a}+\sqrt{(\frac{c}{2a})^2-{(\frac{b}{3a})}^2}}\)

也就是说对于这种情况,根其实也会有一个判别式\(\varDelta =(\frac{c}{2a})^2-{(\frac{b}{3a})}^2\)

当\(\varDelta <0\)时,有一个实根与两个复根

当\(\varDelta =0\)时,有三个实根.当\(b=c=0\)时,有三个相等的根.当\(b\neq 0或c\neq 0\)时,三个实根中有两个相等.

当\(\varDelta >0\)时,有三个不等实根.

这个解法本质上就是把前面猜出来的一个根变成实际可求的\(m+n\),算法重点放在构造和求取\(m+n\)上