2020牛客寒假算法基础集训营3
这套题稍微难一点点。
题目大意:给你一个n*m的迷宫,每个格子有三种可能的状态,‘R’代表只能向右走,‘D'代表只能向下走,’B'代表既可以向右走又可以向下走,然后问到达(n,m)这个位置时的方案数对1e9+7取模之后==k这种迷宫,如果无解输出No solution。
解题:
这个题目是一个构造题,首先可以看一下这个图片。
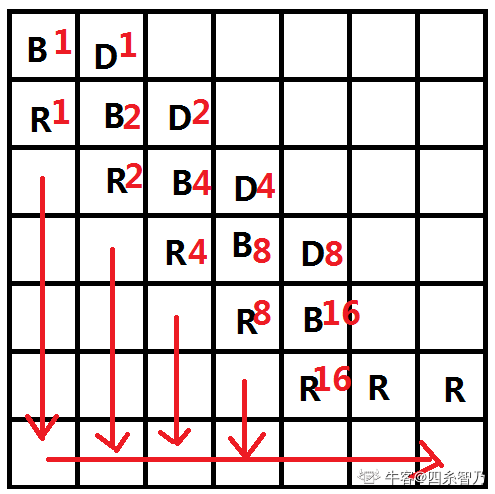
容易发现如果在主斜对角线上全部标记成B,在主斜对角线的上面一条对角线全部标记成D,在主斜对角线的下面一条对角线全部标记成R,那么主斜对角线是不是就是2^0,2^1,2^2...
对于一个数k,将k先转化成二进制,如果二进制的第i位存在,则找到1<<i 在主对角线的位置,然后把这个位置下面的R改成B,然后一路传下去即可。
因为k是对1e9+7取完膜之后的数,所以k<1e9+7。
所以k一定可以转化成满足条件的二进制。
这个题目有一个比较坑的点(对于我这种写法)就是k==0的时候,这个时候我们要把k看出k==1e9+7。

#include<queue> #include<cstring> #include<iostream> #include<algorithm> #include<cstdio> #include<cmath> using namespace std; typedef long long ll; const int maxm=2e5+7; const int mod=1e9+7; int a[100]; char s[55][55]; int main(){ int k,pos=0; scanf("%d",&k); if(k==0) k=1e9+7; while(k) a[++pos]=(k&1),k>>=1; int n=pos+1,m=pos; printf("%d %d\n",n,m); s[n][m]='B'; for(int i=1;i<=n;i++) for(int j=i+1;j<=m;j++) s[i][j]='D'; for(int i=1;i<=n;i++) for(int j=1;j<i;j++) s[i][j]='R'; for(int i=1;i<=min(n,m);i++) s[i][i]='B'; for(int i=1;i<=pos;i++){ if(a[i]){ for(int j=i+1;j<=n;j++) s[j][i]='D'; s[i+1][i]='B'; } } for(int j=1;j<=m;j++) s[n][j]='B'; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ printf("%c",s[i][j]); } printf("\n"); } return 0; }
题目大意:t组输出,t的范围是[1,1e5],每次给你四个数l1,r1,l2,r2.
(1<=l1<=r1<=1e18,1<=l2<=r2<=1e18)
从[l1,r1]娶一个数字a,从[l2,r2]取一个数字b,问a xor b的期望。
为避免精度误差,请输出
数据保证
也就是Q的逆元有意义,并且保证(r1-l1+1)*(r2-l2+1)不是mod的倍数。
解题:
因为要求两个区间的异或值,而且这个区间范围非常大。
然后发现区间异或值可以等效于把这个区间拆成二进制。
第一个区间个位上为1的个数是num11,为0的个数num10,第二个区间个位上为1的个数num21,为0的个数是num20,所以解就是(num11 * num20+num21 * num10)*2^0,
所以在十位上同理,只是*2^1。
然后就是要求一个区间在每一位上0的个数和1的个数。
这个就要用到数位dp了。
求完之后,就是一个费马小定理求逆元,求出区间长度相乘的逆元即可。
我觉得我肯定是很久没有写过数位dp了,这个数位dp居然没有写出来,伤心ing。

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int mod=1e9+7; ll dp[100][100][2],a[100]; ll dfs(int pos,int num,bool limit,bool f){ if(pos==-1) return f; if(!limit&&dp[pos][num][f]!=-1) return dp[pos][num][f]; int up=limit?a[pos]:1; ll ans=0; for(int i=0;i<=up;i++){ ans+=dfs(pos-1,num,limit&&(i==up),f||((pos==num)&&i)); } if(!limit) dp[pos][num][f]=ans; return ans; } ll solve(ll x,int k){ int pos=0; while(x){ a[pos++]=x&1; x>>=1; } return dfs(pos-1,k,1,0); } long long inv(long long x,long long mod) { long long k=mod-2,ans=1; while(k) { if (k&1) ans=ans*x%mod; x=x*x%mod; k>>=1; } return ans; } int main(){ memset(dp,-1,sizeof(dp)); int t;scanf("%d",&t); while(t--){ ll l1,l2,r1,r2,ans=0; scanf("%lld%lld%lld%lld",&l1,&r1,&l2,&r2); for(ll i=0,p=1;i<64;i++,p*=2){ ll num1=(solve(r1,i)%mod-solve(l1-1,i)%mod+mod)%mod; ll num2=(solve(r2,i)%mod-solve(l2-1,i)%mod+mod)%mod; ans+=((r2-l2+1-num2)%mod*num1%mod+(r1-l1+1-num1)%mod*num2%mod)*(p%mod); ans%=mod; } //ans=((ans%mod)+mod)%mod; ans=(ans*inv((r2-l2+1)%mod*((r1-l1+1)%mod)%mod,mod))%mod; printf("%lld\n",ans); } return 0; }
题目大意:有一幅图n个点,m条双向路,路径长度均为1,牛牛初始位置在1号点,接下来会出现k只宝可梦,已知每只宝可梦出现的时间地点以及该宝可梦的战斗力,并且不存在任何一个时刻同时刷出两只及以上的宝可梦。如果在宝可梦刷新时,牛牛恰好在那个路口,那么他一定可以抓到那只宝可梦。问他能够捕获的宝可梦战斗力之和最大是多少?
解题:
这个题目时间是线性的,所以我们要根据时间来求能够捕获的宝可梦战斗力之和。
假设dp[i]表示在第i时刻能够得到的最大战斗力。
但是因为i的范围是[1,1e9],所以这样明显是不对的,所以自然而然可以想到离散化,dp[i]表示a[i].t时刻的最大战斗力。
转移是m^2的,但是因为一共只有200个点,所以说明200s肯定可以走到地图上的任意一个点,所以可以优化成200*m。
这个怎么写呢?就是在200s以内就直接暴力转移,然后求前200的前缀max,第i这个点就可以直接从前缀max转移。
转移的限制是时间,所以我们首先要求出任意两个点之间的最短距离,这个可以用floyd来求。然后转移判断两点之间的距离是不是小于这两个点出现宝可梦的时间差,小于则可以转移,这个是暴力转移。因为200s可以到达任意地方,所以就没有这个限制,可以直接求一个前缀max转移。
这个题目还需要注意一点的是,要把dp初始化为-inf64,原因很简单,因为如果这个时刻没有任何点可以到达,那么如果初始化为0,则之后可能从这个点进行转移更优,即使这个点0贡献,但是实际上来说是无法从这个点转移的,这个点是一个非法状态。所以说要初始化为-inf64 表示无法从这个点转移。

#include <bits/stdc++.h> #define inf 0x3f3f3f3f #define inf64 0x3f3f3f3f3f3f3f3f using namespace std; typedef long long ll; const int mod=1e9+7; const int maxn=1e5+10; ll dp[maxn],dis[220][220]; struct node{ int t,p,val; node(int t=0,int p=0,int val=0):t(t),p(p),val(val){} }a[maxn]; bool cmp(node a,node b){ return a.t<b.t; } int main(){ int n,m,k; scanf("%d%d",&n,&m); memset(dis,inf,sizeof(dis)); for(int i=1;i<=m;i++){ int u,v; scanf("%d%d",&u,&v); dis[u][v]=dis[v][u]=1; } for(int i=1;i<=n;i++) dis[i][i]=0; for(int h=1;h<=n;h++){ for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ dis[i][j]=min(dis[i][j],dis[i][h]+dis[h][j]); } } } scanf("%d",&k); for(int i=1;i<=k;i++){ int t,p,val; scanf("%d%d%d",&t,&p,&val); a[i]=node(t,p,val); } sort(a+1,a+1+k,cmp); ll premaxn=0,ans=0; a[0]=node(0,1,0); for(int i=1;i<=k;i++){ if(i>200){ premaxn=max(premaxn,dp[i-200]); dp[i]=premaxn+a[i].val; } else dp[i]=-inf64; for(int j=1;j<=200&&i-j>=0;j++){ if(a[i].t-a[i-j].t>=dis[a[i].p][a[i-j].p]){ dp[i]=max(dp[i],dp[i-j]+a[i].val); } } ans=max(ans,dp[i]); } printf("%lld\n",ans); return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号