组合数学学习笔记

算是对近几周来组合数学学习笔记的一个大整合吧。

1.1 - 计算的基本原则

定义一个集合 \(A=\{a_1,\dots,a_n\}\)，\(|A|\) 为集合中元素的个数。则它满足以下原则：

1 相等原则

如果存在两个集合 \(A,B\)，存在 \(F: A\mapsto B\) 且一一对应，则 \(|A|=|B|\)。

例 1.1.1：\(n\) 名选手参加乒乓球比赛，赛制采用单打淘汰赛，问需要打多少场决出冠军。

解：

设 \(A\) 为全部比赛集合，即 \(a\in A\)，表示 \(a\) 是某一场比赛。\(B\) 是除冠军外的所有选手的集合，存在 \(F: A\mapsto B\)，即 \(F(a)=b\)。
因此，\(|A|=|B|=n-1\)。

2 加法原则

设 \(A\) 是有限集合 \(A_i\subseteq A(i=1,2,\dots,k)\)，如果 \(A=\bigcup\limits_{i=1}^k A_i\)，且 \(\forall i,j\)，\(A_i\cap A_j=\varnothing\)，则 \(A=\sum\limits_{i=1}^k |A_i|\)。

并集：\(A\cup B\)，\(A,B\) 中元素合并，重复的保留 \(1\) 次。或者也可以这么说：存在于 \(A\) 或者存在于 \(B\) 中的所有元素构成的集合。
交集：\(A\cap B\)，同时存在 \(A,B\) 中。

例 1.1.2：设 \(n\) 是大于 \(1\) 的正整数，求满足条件 \(x+y\leqslant n\) 的所有正整数对 \((x,y)\) 的个数。

解：

设所有满足条件的数对为 \(A\)，则题目可以转化为求 \(|A|\)。
\(|A|=\sum\limits_{i=1}^n A_i\)，其中 \(A_i\) 表示其集合中数对 \(x\) 均取 \(i\) 的个数。
\(A_i=\{(i,1),(i,2),\dots,(i,n-i)\}\)，那么显然 \(|A_i|=n-i\)。
\(\begin{aligned}\therefore |A|&=\sum\limits_{i=1}^n|A_i|\\&=\sum\limits_{i=1}^n(n-i)\\&=(n-1)+(n-2)+\dots+1\\&=\dfrac{n(n-1)}2\end{aligned}\)

例 1.1.3：把 \(4\) 个人分成两组，每组至少 \(1\) 人，求不同的分组方式。

解：

设所有分组方式构成的集合为 \(A\)，则题目又可以转化为求 \(|A|\)。
显然，\(A=A_1+A_2\)。
其中：\(A_i\) 表示有一组含有 \(i\) 人。
设四个人分别为甲乙丙丁。
则显然，\(|A_1|=4,|A_2|=3\)，其中 \(A_2=\{(\text{甲乙},\text{丙丁}),(\text{甲丙},\text{乙丁}),(\text{甲丁},\text{乙丙})\}\)。
\(\therefore |A|=|A_1|+|A_2|=4+3=7\)。

3 乘法原则

定义 1.1.1：已知做一件事情要分两步，完成第一步有 \(m\) 种方法，完成第二步有 \(n\) 种方法，则做这件事情有 \(m\cdot n\) 种方法。

乘法原则：已知完成一件事有 \(k\) 个步骤，且已经完成了前 \(i-1(1\leqslant i\leqslant k)\) 个步骤下，完成第 \(i\) 个步骤有 \(n_i\) 种方法，则做这件事情有 \(\prod\limits_{i=1}^k n_i\) 种方法。

例 1.1.4：求 \(n\) 个元素的集合 \(A=\{a_1,a_2,\dots,a_n\}\) 的子集的个数。

解：

将求解子集的过程分成 \(n\) 步，第 \(i\) 步指的是是否将第 \(i\) 个元素 \(a_i\) 放入子集中，这有两种方式。则子集总数为 \(\begin{matrix}\underbrace{2\times 2\times\dots\times 2}\\n\text{ 个 }2\end{matrix}=2^n\)。

例 1.1.5：求万位数字不是 \(5\) 且个位数不相同的所有五位数个数 \(N\)。

解：

形成该五位数的过程看成从万位到个位依次形成。其中万位有 \(8\) 种可能，千位有 \(9\) 种可能，百位有 \(8\) 种可能，十位有 \(7\) 种可能，个位有 \(6\) 种可能。
\(\therefore N=8\times 9\times 8\times 7\times 6=24192\)。

例 1.1.6：设自然数 \(n\) 的质因数分解式 \(n=p_1^{n_1}p_2^{n_2}\dots p_k^{n_k}\)，求 \(n\) 的不同正约数的个数 \(N\)。

解：

设 \(P=p_1^{a_1}p_2^{a_2}\dots p_k^{a_k}\)，其中 \(0\leqslant a_i\leqslant n_i\)。
显然 \(P\mid n\)。
则由乘法原则：\(N=(n_1+1)(n_2+1)\dots (n_k+1)=\prod\limits_{i=1}^k (n_i+1)\)。

1.2 - 排列

定义 1.2.1：设 \(A\) 是 \(n\) 个元素构成的集合，即 \(A=\{a_1,a_2,\dots,a_n\}\)，若序列 \(a_1,a_2,\dots,a_r\) 是由来自 \(A\) 的 \(r\) 个元素构成的且彼此互不相同，则称序列 \(a_1,a_2,\dots,a_r\) 是 \(A\) 的一个 \(r\) 排列。

定义 1.2.2: \(n\) 个元素构成集合 \(A=\{a_1,a_2,\dots,a_n\}\) 的 \(n\) 排列，称为 \(A\) 的全排列。

定义 1.2.3：设 \(n,r(n\geqslant r)\) 是正整数，\(P_n^r\) 表示从 \(n\) 个数拿出 \(r\) 个数构成的排列数。则
\(\begin{aligned}P_n^r&=n(n-1)(n-2)\dots(n-r+1)\\&=\dfrac{n!}{(n-r)!}\end{aligned}\)

推论：\(P_n^n=n!\)。

例 1.2.1：求 \(n\) 个不同数 \(a_1,a_2,\dots,a_n\) 构成的 \(a_1\) 与 \(a_2\) 不相邻的全排列个数。

解：

设 \(a_1\) 与 \(a_2\) 不相邻的全排列集合为 \(A\)，则问题可以转化为求 \(|A|\)。
设 \(B\) 为全排列集合 \(B=A+C\)。其中 \(C\) 为 \(a_1\) 与 \(a_2\) 相邻的全排列构成的集合。
则 \(n!=|B|=|A|+|C|\)。
\(\therefore n!=|A|+2\times (n-1)!\)。
\(\begin{aligned}\therefore |A|&=n!-2\times(n-1)!\\&=n\times(n-1)!-2\times(n-1)!\\&=(n-2)\times(n-1)!\end{aligned}\)

例 1.2.2：设由 \(1,2,3,4,5,6\) 组成的，数字互不相通的四个偶数个数为 \(n\)，它们的和为 \(m\)，求 \(n,m\)。

解：

找偶数个位只能够是 \(2,4,6\)，剩余三位从剩下的五个数字选择排列，其排列数为 \(P_5^3\)，则
\(\begin{aligned}n&=3\times P_5^3\\&=3\times(5\times 4\times 3)\\&=180\end{aligned}\)
\(m=a_1+10a_2+100a_3+1000a_4\)，其中
\(a_1=(2+4+6)P_5^3=720\)，\(a_2=a_3=a_4=(1+3+5)\times P_4^2+(2+4+6)\times P_4^2=612\)。
\(\therefore m=720+612\times (10+100+1000)=680040\)。

2.1 - n 元集合 r - 可重复排列

定义 2.1.1：设 \(A\) 是 \(n\) 个元素构成的集合，如果序列 \(a_1,a_2,\dots,a_r\) 的元素均来自于 \(A\)，且有可能他们出现了相同的元素，则成旭烈 \(a_1,a_2,\dots,a_r\) 为 \(n\) 元集 \(A\) 的 \(r~-\) 可重复排列。

定理 2.1.1：\(n\) 元集的 \(r~-\) 可重复排列的个数为 \(n^r\)。

例 2.1.1：有 \(1,2,3,4,5,6\) 可以组成多少个大于 \(35000\) 的五位数？

解：

分类讨论一下：

（1）万位数字为 \(4,5,6\)，则一共可能的数字有 \(3\times 6^4=3888\) 个。
（2）万位数字为 \(3\)，则千位数字必须 \(\geqslant 5\)，则一共可能的数字一共有 \(2\times 6^3=432\) 个。

所以这样的五位数一共有 \(3888+432=4320\) 个。

2.2 - 多重集的排列

定义 2.2.1：有 \(n_1\) 个 \(a_1\)，\(n_2\) 个 \(a_2\)，\(\dots\)，\(n_k\) 个 \(a_k\) 组成的集合记为 \(M=\{n_1\cdot a_1,n_2\cdot a_2,\dots,n_k\cdot a_k\}\) 称为多重集。\(M\) 的总元素个数为 \(\sum\limits_{i=1}^k n_i\)。

定义 2.2.2：设 \(M=\{n_1\cdot a_1,n_2\cdot a_2,\dots,n_k\cdot a_k\}\)，\(\pi\) 是集合 \(\{a_1,a_2,\dots,a_k\}\) 的一个 \(n~-\) 可重复排列，若 \(\pi\) 中有 \(n_1\) 个 \(a_1\)，\(n_2\) 个 \(a_2\)，\(\dots\)，\(n_k\) 个 \(a_k\)。称 \(\pi\) 是多重集 \(M\) 的一个全排列。

定理 2.2.1：多重集 \(M=\{n_1\cdot a_1,n_2\cdot a_2,\dots,n_k\cdot a_k\}\) 的全排列个数 \(N=\dfrac{(\sum\limits_{i=1}^k n_i)!}{\prod\limits_{i=1}^k n_i!}\)。

定义 2.2.3：设 \(M=\{n_1\cdot a_1,n_2\cdot a_2,\dots,n_k\cdot a_k\}\)，\(A=\{s_1\cdot a_1,s_2\cdot a_2,\dots,s_k\cdot a_k\}\)，其中 \(0\leqslant s_i\leqslant n_i\)。我们称 \(A\) 是 \(M\) 的一个子集。进一步，设 \(r=\sum\limits_{i=1}^k s_i\)，称 \(A\) 是 \(M\) 的 \(r~-\) 子集。由 \(r~-\) 子集中元素构成的排列称为 \(r~-\) 排列。

例 2.2.1：求多重集 \(M=\{5\cdot a,3\cdot b\}\) 的 \(6~-\) 排列个数。

解：

不难发现 \(6~-\) 排列具体可分类成：\(\begin{cases}\{5\cdot a,b\}\\\{4\cdot a,2\cdot b\}\\\{3\cdot a,3\cdot b\}\end{cases}\)。则可以直接根据公式可以求得：

• 排列 \(\{5\cdot a,b\}\) 的个数为 \(\dfrac{6!}{5!\cdot 1!}=6\)。
• 排列 \(\{4\cdot a,2\cdot b\}\) 的个数为 \(\dfrac{6!}{4!\cdot 2!}=15\)。
• 排列 \(\{3\cdot a,3\cdot b\}\) 的个数为 \(\dfrac{6!}{3!\cdot 3!}=20\)。

因此排列总数为 \(6+15+20=41\)。

2.3 T 路

定义 2.3.1：由 \(p\times q\) 各单位正方形拼成的长为 \(p\)，宽为 \(q\) 的长方形称为 \(p\times q\) 棋盘。

定理 2.3.1：沿 \(p\times q\) 棋盘上的线段由顶点 \(A\) 到顶点 \(B\) 的最短路的数量为 \(\dfrac{(p+q)!}{p!\cdot q!}\)。

定义 2.3.2：在 \(p\times q\) 棋盘中，由任意点位置 \((x,y)\) 移动到 \((x+1,y+1)\) 或 \((x+1,y-1)\) 的有向线段称为一个 \(T\) 步。

定义 2.3.3：定义一个从点 \(A\) 到点 \(B\) 的一条 \(T\) 路指的是由若干个 \(T\) 步组成的起点 \(A\) 到终点 \(B\) 的有向折线。

定理 2.3.2：若存在从点 \(A(a,\alpha)\) 到点 \(B(b,\beta)\) 的 \(T\) 路，则必然满足以下三个条件：

\(\begin{cases}b>a\\b-a\geqslant |\beta-\alpha|\\a+\alpha\equiv b+\beta\pmod 2\end{cases}\)
（第三个条件说简单点就是 \(a+\alpha\) 和 \(b+\beta\) 具有相同的奇偶性。）

定理 2.3.3：设起点 \(A(a,\alpha)\) 到终点 \(B(b,\beta)\) 存在 \(T\) 路，则 \(T\) 路的条数为 \(\dfrac{(b-a)!}{(\dfrac{b-a}{2}+\dfrac{\beta-\alpha}{2})!(\dfrac{b-a}{2}-\dfrac{\beta-\alpha}{2})!}\)。

定理 2.3.4：反射定理

设 \(A(a,\alpha)\) 到 \(B(b,\beta)\) 满足 \(T\) 条件，且 \(\alpha,\beta>0\)，\(b-a\geqslant\alpha+\beta\)，则由 \(A\) 到 \(B\) 经过 \(x\) 轴（即横坐标为 \(0\)）的 \(T\) 路条数等于由 \(A'(a,-\alpha)\) 到 \(B\) 的 \(T\) 路条数：\(\dfrac{(b-a)!}{(\dfrac{b-a}{2}+\dfrac{\beta+\alpha}{2})!(\dfrac{b-a}{2}-\dfrac{\beta+\alpha}{2})!}\)。

定理 2.3.5：设 \(A(a,\alpha)\) 到 \(B(b,\beta)\) 满足 \(T\) 条件，且 \(\alpha,\beta>0\)，\(b-a\geqslant\alpha+\beta\) 则由 \(A\) 到 \(B\) 不经过 \(x\) 轴（即横坐标为 \(0\)）的 \(T\) 路条数为 \(\dfrac{(b-a)!}{(\dfrac{b-a}{2}+\dfrac{\beta-\alpha}{2})!(\dfrac{b-a}{2}-\dfrac{\beta-\alpha}{2})!}-\dfrac{(b-a)!}{(\dfrac{b-a}{2}+\dfrac{\beta+\alpha}{2})!(\dfrac{b-a}{2}-\dfrac{\beta+\alpha}{2})!}\)。

例 2.3.1：甲乙两人比赛乒乓球，最终比分为 \(21:17\)，求在比赛过程中，甲都领先于乙的计分情况的数量。

解：

计分可以变成一个序列 \(a_1,a_2,\dots,a_{38}\)（打了 \(38\) 局比赛所以到 \(a_{38}\)），其中 \(a_j=\begin{cases}1&\text{第 j 个球甲得分}\\-1&\text{第 j 个球乙得分}\end{cases}\)。
记 \(A_j\) 表示为 \((j,\sum\limits_{k=1}^j a_k)(1\leqslant j\leqslant 38)\)。则比赛计分情形可以用一个有向折线 \(A_1,A_2,\dots,A_{38}\) 表示比赛结果。
由于甲一直要领先乙，所以这就意味着任意 \(A_j\) 的纵坐标 \(\sum\limits_{k=1}^j a_k>0\)。则问题就可以转化为求 \(A(1,1)\) 到 \(B(38,4)\)（因为甲最后领先乙 \(4\) 分）的且不经过 \(x\) 轴的 \(T\) 路数量。则直接可以套用定理 2.3.5 的公式可得结果为
\(\begin{aligned}\dfrac{(38-1)!}{(\dfrac{38-1}{2}+\dfrac{4-1}{2})!(\dfrac{38-1}{2}-\dfrac{4-1}{2})!}-\dfrac{(38-1)!}{(\dfrac{38-1}{2}+\dfrac{4+1}{2})!(\dfrac{38-1}{2}-\dfrac{4+1}{2})!}&=\dfrac{37!}{20!\cdot 17!}-\dfrac{37!}{21!\cdot 16!}\\&=270391268070\end{aligned}\)

2.4 组合

定义 2.4.1：集合 \(A\) 中含有 \(r\) 个元素的子集，称为 \(A\) 的 \(r~-\) 子集。若 \(A\) 中有 \(n\) 个元素，则集合 \(A\) 的 \(r~-\) 子集（其中元素均不相同）的个数用 \(C_n^r\) 或者 \(\begin{pmatrix}n\\r\end{pmatrix}\) 表示 \(n\) 个元素取 \(r\) 个元素的方案数。

定义 2.4.2：设 \(n\) 为正整数，\(r\) 为非负整数，则 \(C_n^r=\begin{cases}0&r>n\\\dfrac{n!}{r!(n-r)!}&r\leqslant n\end{cases}\)。

附另一种表达：\(C_n^r=\dfrac{n(n-1)\dots(n-r+1)}{1\times2\times3\times\dots\times r}\)。

• \(n\) 元集的 \(r~-\) 可重复集合
  定义 2.4.3：从集合 \(A\) 中可重复地选取 \(r\) 个元素组成的多重集——\(r~\) 可重复集。
  设 \(A=\{a_1,a_2,\dots,a_n\}\)，取 \(A_r=\{x_1\cdot a_1,x_2\cdot a_2,\dots,x_n\cdot a_n\}\)。则有 \(\sum\limits_{i=1}^nx_i=r\)，且 \(\forall i\in[1,n]\)，都有 \(0\leqslant x_i\leqslant r\)。
  定理 2.4.1：\(n\) 元集的 \(r~-\) 可重复组合的个数为 \(C_{n+r-1}^r\)。
  推论 1：对于不定方程 \(\sum\limits_{i=1}^nx_i=r\)，其非负整数解有 \(C_{n+r-1}^r\) 个。
  推论 2：对于不定方程 \(\sum\limits_{i=1}^nx_i=r(r\geqslant n)\)，其正整数解有 \(C_{r-1}^{r-n}\) 个。（证明提示：令 \(y_i=x_i-1\)，则方程变为 \(\sum\limits_{i=1}^n y_i=r-n\)，然后就可以变成求这个不定方程的非负整数解的个数了。）

例 2.4.1：求把 \(r\) 件相同的物品分给 \(n\) 个人不同的分法数。

解：

设第 \(i(1\leqslant i\leqslant n)\) 个人分到物品 \(x_i\) 件，显然有 \(x_i\geqslant 0\)，则问题可以转化为：\(\begin{cases}\sum\limits_{i=1}^n x_i=r\\0\leqslant x_i\leqslant r\end{cases}\)。因此根据定理 2.4.1 的推论 1 可以求出分法有 \(C_{n+r-1}^r\) 个。

例 2.4.2：把 \(r\) 件相同的物品分给 \(n\) 个人，要求每个人至少分到一件物品，问有多少种分法。

解：

设第 \(i(1\leqslant i\leqslant n)\) 个人分到 \(x_i\) 件物品，根据题意有 \(x_i\geqslant 1\)，则问题转化为 \(\begin{cases}\sum\limits_{i=1}^nx_i=r\\\forall i\in[1,n],x_i\geqslant 1\end{cases}\)。因此，问题转化为求上述不定方程的正整数解数。根据定理 2.4.1 的推论 2 可求出答案为 \(C_{r-1}^{r-n}\)。

• 组合的一些基本性质
  定理 2.4.2：\(C_n^k=\dfrac{n!}{k!(n-k)!}=\dfrac{n!}{(n-k)!(n-(n-k))!}=C_n^{n-k}\)
  定理 2.4.3：\(\begin{cases}C_n^k=C_{n-1}^k+C_{n-1}^{k-1}(n>k\geqslant 1)\\C_n^k=\dfrac nkC_{n-1}^{k-1}\\C_n^k=\dfrac {n-k+1}k C_n^{k-1}\\C_n^k=\dfrac n{n-1}C_{n-1}^k\end{cases}\)
  定理 2.4.4：\(C_n^mC_m^k=C_n^kC_{n-k}^{m-k}=(n\geqslant m\geqslant k)\)

• 多项式定理
  定理 2.4.5：设 \(n\in\mathbb Z^+\)，\(x_1,x_2,\dots,x_n\) 是正实数，则 \((\sum\limits_{i=1}^n x_i)^n=\sum\limits_{\sum\limits_{i=1}^k n_i=n}\dfrac{n!}{\prod\limits_{i=1}^k n_i!}\prod\limits_{i=1}^k x_i^{n_i}\)。其中 \(\forall i\in[1,n]\)，\(n_i\) 是非负整数。
  推论 1（二项式定理）：\((x+y)^n=\sum\limits_{k=0}^nC_n^k x^k y^{n-k}\)。
  推论 2：\((1+x)^n=\sum\limits_{k=0}^n C_n^k x^k\)。
  推论 3：\(2^n=\sum\limits_{k=0}^n C_n^k\)。
  推论 4：\(\sum\limits_{k=0}^n C_n^k (-1)^k=C_n^0-C_n^1+C_n^2-C_n^3\dots+(-1)^nC_n^n=0\)。

例 2.4.3：求 \((1+2x+3x^2+4x^3)^5\) 的展开式中 \(x^5\) 项的系数。

解：

\(\begin{aligned}(1+2x+3x^2+4x^3)^5&=[(1+x)^2+2x^2(1+2x)]^5\\&=(1+x)^{10}+10x^2(1+x)^8(1+2x)+40x^4(1+x)^6(1+2x)^2+80x^6(1+x)^4(1+2x)^3+\dots\end{aligned}\)
则 \(x^5\) 系数 \(C_{10}^5+10(C_8^3+2C_8^2)+40(C_6^1+2C_2^1)=1772\)。

2.5 容斥原理

设 \(A\) 是具有有限个元素的集合。\(A_i\subseteq A(1\leqslant i\leqslant n)\)。要求 \(\bigcup\limits_{i=1}^n A_i=A,A_i\cap A_j=\varnothing(1\leqslant i<j\leqslant n)\)，自然地，\(|A|=\sum\limits_{i=1}^n|A_i|\)。

定理 2.5.1：设 \(S\) 是有限集，且 \(A,B\subseteq S\)，则：

1. \(|S-A|=|S|-|A|\)，\(|S-B|=|S|-|B|\)。
2. \(|A-B|=|A|-|A\cap B|\)。
3. \(|A\cup B|=|A|+|B|-|A\cap B|\)。
4. \(|S-A\cup B|=|S|-|A|-|B|+|A\cap B|\)。

定理 2.5.2：设 \(S\) 是有限集，且 \(A,B,C\subseteq S\)，则：

1. \(|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|\)。
2. \(|S-A\cup B\cup C|=|S|-|A|-|B|-|C|+|A\cap B|+|A\cap C|+|B\cap C|-|A\cap B\cap C|\)。

定理 2.5.3：设 \(n,k\) 是正整数，\(S=\{1,2,3,\dots,n\}\)，则 \(S\) 中能被 \(k\) 整除个数为 \(\left\lfloor\dfrac nk\right\rfloor\)。

例 2.5.1：求从 \(1\) 到 \(300\) 的整数中有多少个整数能被 \(7\) 整除且能被 \(2\) 或 \(5\) 整除。

解：

设 \(S=\{1,2,\dots,300\}\)，\(A\) 表示 \(S\) 中能被 \(7\times 2=14\) 整除的数的集合，\(B\) 表示 \(S\) 中能被 \(7\times 5=35\) 整除的数的集合，显然 \(A,B\subseteq S\)。则问题转化为求 \(|A\cup B|\)。
\(\therefore |A\cup B|=|A|+|B|-|A\cap B|\)，而 \(|A|=\left\lfloor\dfrac {300}{14}\right\rfloor=21,|B|=\left\lfloor\dfrac {300}{35}\right\rfloor=8,|A\cap B|=\left\lfloor\dfrac {300}{\operatorname{lcm}\{14,35\}}\right\rfloor=4\)。
\(\therefore |A\cup B|=21+8-4=25\)。

例 2.5.2：求从 \(1\) 到 \(1000\) 的整数中有多少个书能被 \(2\) 整除，但不能被 \(3\) 也不能被 \(5\) 整除。

解：

设 \(S=\{1,2,\dots,1000\}\)，\(A\) 表示 \(S\) 中能被 \(2\) 整除元素集合，\(B\) 表示 \(S\) 中能被 \(3\) 整除元素集合，\(C\) 表示 \(S\) 中能被 \(5\) 整除元素集合，显然 \(A,B,C\subseteq S\)，则问题转化为求 \(|A-B\cup C|\)。
\(\therefore\) \(\begin{aligned}|A-B\cup C|&=|A|-|A\cap(B\cup C)|\\&=|A|-|(A\cap B)\cup(A\cap C)\\&=|A|-|A\cap B|-|A\cap C|+|A\cap B\cap C|\end{aligned}\)
而 \(|A|=\left\lfloor\dfrac {1000}{2}\right\rfloor=500,|A\cap B|=\left\lfloor\dfrac {1000}{2\times 3}\right\rfloor=166,|A\cap C|=\left\lfloor\dfrac {1000}{2\times 5}\right\rfloor=100,|A\cap B\cap C|=\left\lfloor\dfrac {1000}{2\times 3\times 5}\right\rfloor=33\)。
\(\therefore |A-B\cup C|=500-166-100+33=267\)。

例 2.5.3：求由 \(n\) 个不同元素 \(a_1,a_2,\dots,a_n\) 组成的 \(a_1\) 与 \(a_2\) 不相邻，\(a_3\) 与 \(a_4\) 也不相邻的排列个数。

解：

设 \(S\) 是 \(a_1,a_2,\dots,a_n\) 组成的所有排列的集合，显然 \(|S|=n!\)。
另设 \(A\) 表示 \(S\) 中 \(a_1,a_2\) 相邻的排列的集合，\(B\) 表示 \(S\) 中 \(a_3,a_4\) 相邻的排列的集合。则问题转化为求 \(|S-A\cup B|=|S|-|A|-|B|+|A\cap B|\)。
而 \(|A|=2(n-1)!,|B|=2(n-1)!,|A\cap B|=4(n-2)!\)。
\(\begin{aligned}\therefore |S-A\cup B|&=n!-4(n-1)!+4(n-2)!\\&=n(n-1)(n-2)!-4(n-1)(n-2)!+4(n-2)!\\&=(n^2-n-4n+4+4)(n-2)!\\&=(n^2-5n+8)(n-2)!\end{aligned}\)

定理 2.5.4：设 \(S\) 是有限集，\(A_i\subseteq S(1\leqslant i\leqslant n)\)，则
\(\begin{aligned}\bigcup\limits_{i=1}^n A_i&=\sum\limits_{i=1}^n|A_i|-\sum\limits_{1\leqslant i_1<i_2\leqslant n}|A_{i_1}\cap A_{i_2}|\\&+\dots+(-1)^{k-1}\sum\limits_{i\leqslant i_1<i_2<\dots <i_k\leqslant n}|A_{i_1}\cap A_{i_2}\cap\dots\cap A_{i_k}|\\&+\dots+(-1)^{n-1}|A_1\cap A_2\cap\dots\cap A_n|\end{aligned}\)
推论 1：\(|S-\bigcup\limits_{i=1}^n A_i|=|S|-|\bigcup\limits_{i=1}^n A_i|\)。

2.6 笼鸽原理（抽屉原理）和拉姆齐（Ramsey）定理

定理 2.6.1：设 \(A\) 是有限集，\(A_i\subseteq A(1\leqslant i\leqslant n)\)，且 \(\bigcup\limits_{i=1}^n A_i=A\)，则 \(|A|\leqslant\sum\limits_{i=1}^n|A_i|\)。

定理 2.6.2：设 \(A\) 是有限集，\(|A|\geqslant n+1\)，若有 \(A_i\subseteq A(1\leqslant i\leqslant n)\)，且 \(\bigcup\limits_{i=1}^n A_i=A\)，则必有正整数 \(k\in[1,n]\) 使得 \(|A_k|\geqslant 2\)。

例 2.6.1：证明：在一个边长为 \(1\) 的等边三角形中，任取五个点，则必有两个点之间的距离不大于 \(\frac 12\)。

证明：

取三角形三条边的中点相连，将原三角形分解成边长为 \(\frac 12\) 的 \(4\) 个三角形。故根据笼鸽原理可知，必有 \(2\) 个点落在同一个小三角形中，显然其距离小于 \(\frac 12\)。

证毕。

例 2.6.2：证明：从 \(1,2,\dots,2n\) 中任取 \(n+1\) 个不同的数，则这 \(n+1\) 个不同的数中必有两个数，其中一个数是另一个数的倍数。

证明：

设 \(A\) 是从 \(1,2,\dots,2n\) 中任取 \(n+1\) 个数构成的集合。若某一个元素 \(s\in A\)，则 \(s=2^\alpha\cdot\beta\)，其中 \(\beta\) 是奇数且小于 \(2n-1\)。
构造 \(A_i=\{s|s\in A,s=(2i-1)\cdot 2^\alpha,\alpha\geqslant 0,\alpha\in\mathbb Z\}\)。显然 \(A_i\subseteq A(1\leqslant i\leqslant n)\) 且 \(\bigcup\limits_{i=1}^n A_i=A\)，根据定理 2.6.2 必有 \(k\) 满足 \(|A_k|\geqslant 2\)。
设 \(A_k\) 中两个元素为 \((2k-1)\cdot 2^{\alpha_1},(2k-1)\cdot 2^{\alpha_2}\)，显然他们满足倍数关系。

定理 2.6.3：设 \(A\) 是 \(m(\geqslant 2)\) 个元素的集合，\(A_i\subseteq A(1\leqslant i\leqslant n)\) 且 \(\bigcup\limits_{i=1}^n A_i=A\)，则必然有正整数 \(k\in[1,n]\) 使得 \(|A_k|\geqslant\left\lfloor\dfrac {m-1}n\right\rfloor+1\)。

定义 2.6.1：给定平面上 \(n\) 个点，用线段将这些点连接起来，这样的图成为 \(K_n\) 图，要求任意两点之间均有边，则共有 \(C_n^2=\dfrac{n(n-1)}2\) 条边。
用 \(r(\geqslant 2)\) 种颜色去涂 \(K_n\) 图中的边，每条边涂一种颜色，这样的涂色方式称为 \(r-K_n\)。

一些直观结论：

当 \(3\leqslant n\leqslant 5\)，\(2-K_n\) 着色不一定含有三条边颜色相同的三角形，以下从左往右分别给出 \(n=3,4,5\) 时的一种反例：

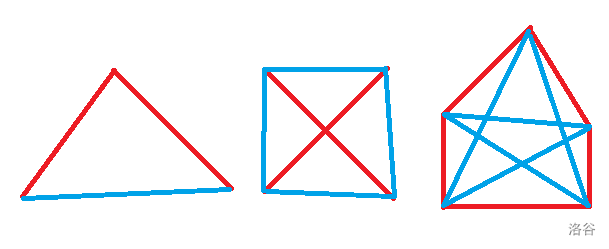
定理 2.6.4：\(2-K_6\) 着色必含有一个单色三角形。
另一种表达形式：假设有 \(6\) 个人，每两个人之间互相握手，则必有 \(3\) 个人，他们或者彼此都握过手或者都没有握过。
推论 1：事实上，当 \(n\geqslant 6\) 时，\(2-K_n\) 着色都必有一个单色三角形。

定理 2.6.5（Ramsey 定理）：
对于给定的三个数 \(p,q,r\) 且 \(p\geqslant r,q\geqslant r\)，总存在一个与 \(p,q,r\) 相关的最小正整数 \(R\)，当有限集 \(|S|\geqslant R\) 时，将 \(T_r(S)\) 分成两部分 \(T_r(S)=\alpha\cup\beta(\alpha\cap\beta=\varnothing)\)，则 \(S\) 中有一个 \(p\) 元子集，其一切 \(r~-\) 子集均属于 \(\alpha\) 或存在 \(q\) 元子集，其一切 \(r~-\) 子集属于 \(\beta\)。

The end.