UVA10079 Pizza Cutting 题解
Content
求用 \(n\) 条直线最多能将平面分成多少块区域。
多组输入,以一个负数结束。
数据范围:\(0\leqslant n\leqslant 2.1\times 10^8\)。
Solution
小学奥数题。
首先你得要知道 \(1+2+...+n=\dfrac{n(n+1)}{2}\)。
我们先通过画图来找一下规律。
- 不切,此时很显然总共有 \(1\) 个区域。

- 切一刀,此时最多有 \(2\) 个区域。
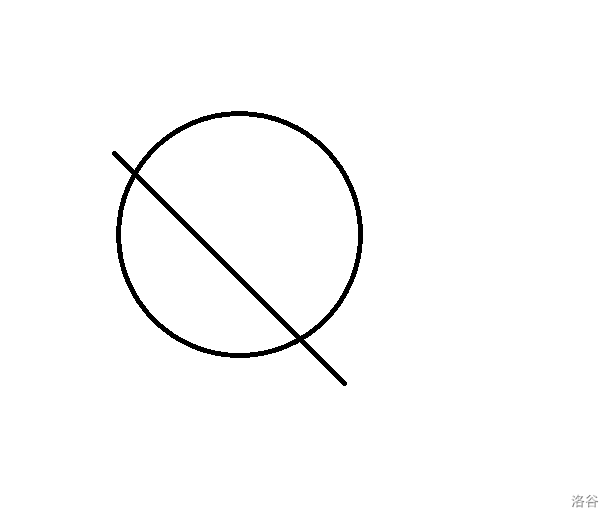
- 切两刀,此时最多有 \(4\) 个区域。
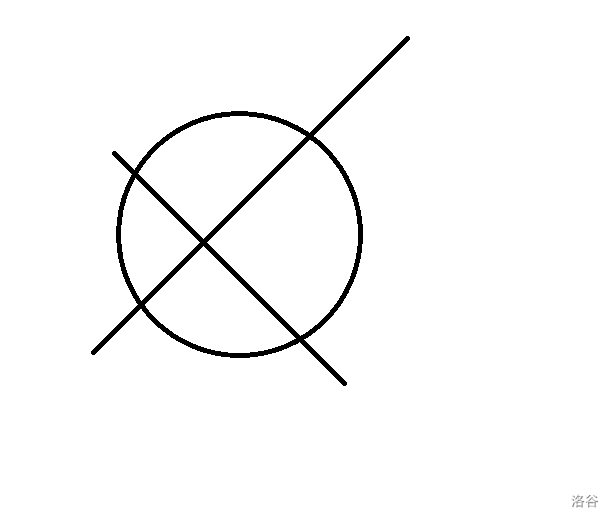
- 切三刀,此时最多只能有 \(7\) 个区域。
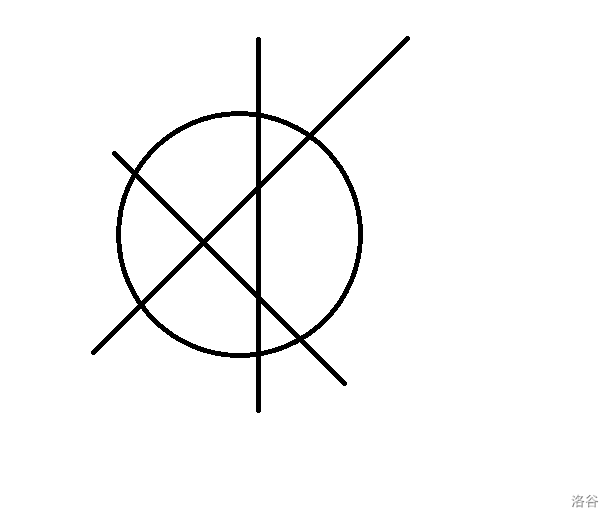
为什么呢?
因为第三条直线最多只能和前面的直线有 \(2\) 个交点,这样直线就分成了三个部分,因此最多只能够新产生 \(3\) 个区域。
类似的,第 \(n\) 条直线最多只能和前面的直线有 \((n-1)\) 个交点,把直线分成 \(n\) 个部分,最多只能够新产生 \(n\) 个区域。
故,\(n\) 条直线最多能将平面分成:\(1+1+2+...+n=1+\dfrac{n(n+1)}{2}\) 个区域。
注意这么大的答案如果只开 \(\texttt{int}\) 的话是肯定要爆的,因此得开 \(\texttt{long long}\)。
Code
#include <cstdio>
#include <algorithm>
using namespace std;
long long n;
int main() {
while(~scanf("%lld", &n) && n >= 0)
printf("%lld\n", n * (n + 1) / 2 + 1);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号