LeetCode 1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix

原题链接在这里：https://leetcode.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/description/

题目：

Given a m x n binary matrix mat. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighbors if they share one edge.

Return the minimum number of steps required to convert mat to a zero matrix or -1 if you cannot.

A binary matrix is a matrix with all cells equal to 0 or 1 only.

A zero matrix is a matrix with all cells equal to 0.

Example 1:

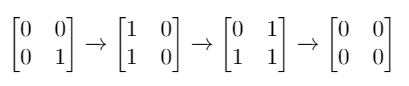
Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:

Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We do not need to change it.

Example 3:

Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix cannot be a zero matrix.

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 3
• mat[i][j] is either 0 or 1.

题解：

The quesiton asks for the minimum number of steps to cover to all 0.

The minimum steps is related to BFS.

In BFS queue, we maintain the current state of matrix.

We can use a integer and bit representation for each state.

If current state == 0, we find the result and return level.

Otherwise, for each (i, j) coordiante, we check all 5 dir, if it is within bound, we flip the value, and get the next. If next is not visited before, add to the queue.

Time Complexity: O(2 ^ (m * n)). m = matrix.length. n = matrix[0].length. There could be 2 ^ (m * n) states.

Space: O(2 ^ (m * n))

AC Java:

class Solution {
    int[][] dirs = new int[][]{{0, 0}, {0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    public int minFlips(int[][] mat) {
        int m = mat.length;
        int n = mat[0].length;
        int state = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                state |= (mat[i][j] << (i * n + j));
            }
        }

        HashSet<Integer> visited = new HashSet<>();
        LinkedList<Integer> que = new LinkedList<>();
        visited.add(state);
        que.add(state);
        int level = 0;

        while(!que.isEmpty()){
            int size = que.size();
            while(size-- > 0){
                int cur = que.poll();
                if(cur == 0){
                    return level;
                }

                for(int i = 0; i < m; i++){
                    for(int j = 0; j < n; j++){
                        int next = cur;
                        for(int [] dir : dirs){
                            int x = i + dir[0];
                            int y = j + dir[1];
                            if(x >= 0 && x < m && y >= 0 && y < n){
                                next ^= (1 << (x * n + y));
                            }
                        }

                        if(!visited.contains(next)){
                            visited.add(next);
                            que.add(next);
                        }
                    }
                }
            }

            level++;
        }

        return -1;
    }
}