【HEVC帧间预测论文】P1.8 Complexity Control of High Efficiency Video Encoders for Power-Constrained Devices

参考：Complexity Control of High Efficiency Video Encoders for Power-Constrained Devices

《HEVC标准介绍、HEVC帧间预测论文笔记》系列博客，目录见：http://www.cnblogs.com/DwyaneTalk/p/5711333.html

2011 期刊

 

核心思想：

        通过以frame为单位，限制帧内每个CU的最大depth来实现对视频序列编码复杂度的控制。

思路分析：

        实验环境：HM2， low delay and low complexity， 1280*768  504-frames Basketball、BQTerrace and Cactus video sequence。64-bits and 2.27GHz CPU

        复杂度(computional complexity)衡量：通过特殊的检测软件分析器(software profiler)统计编码过程中，各个部分消耗的时间。

        图1、不同CU深度在编码中所占复杂度比例

       

如图1：统计的是视频序列中，对于64x64的CTU编码过程中，depth=1、2、3和4 对应的CU块的编码复杂度。灰色区域是对应depth下的CU进行帧间预测复杂度，黑色是对应depth下其他操作的复杂度。编码64x64的CTU时，在CTU的树形结构中depth=1对应的32x32的CU进行帧间预测复杂度占据整个CTU的编码复杂的14.6%，对应depth=2、3和4时，占据的整个CTU复杂度比例分别是15%、17.4%和47.2%。

        上图数据说明：在CTU的递归编码过程中，随着depth的增加，所需要的计算复杂度逐渐增加，特别是当depth为4时，此时CU size为8*8，由于一个64*64的CTU，包含64个8*8的CU，所以在不进行加速优化时，depth占据将近一般的计算复杂度，因此限制CTU的maxinum depth是本论文的核心和出发点。

图2、视频序列中co-location的CTU实际编码深度的连续性       

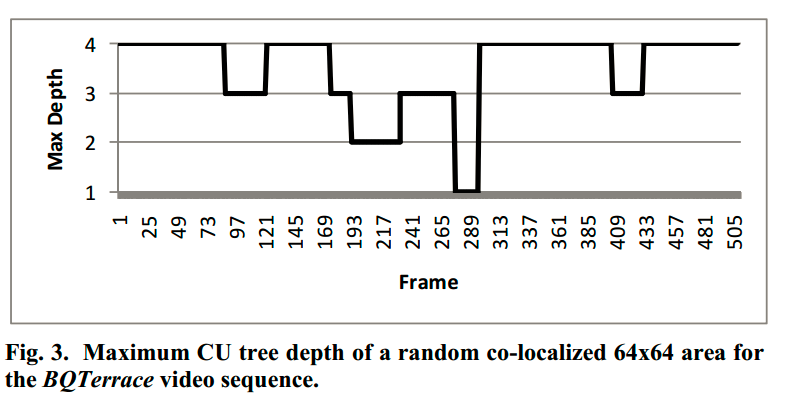
如图2：显示了对于BQTerrace视频序列，对于505个frame中随意某个位置的CTU的编码深度变化，可以看出：1、编码过程中编码深度为4的frame约50%左右，有很大的复杂度优化空间；2、CTU编码深度在时域上有很大的temporal consistency，最小的两次CTU depth变化也在20帧以上，这个特性为预测优化CTU深度提供前提和优化空间。

算法介绍：

        总体思想：

图3、视频序列编码过程中控制示意图

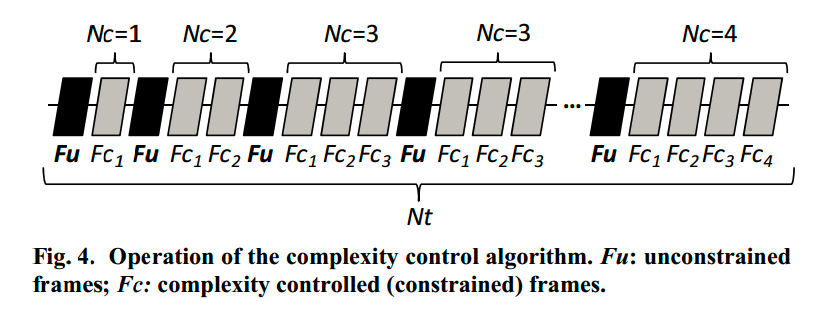
        Fu(unconstrained frame)：不加深度限制的帧，视频序列第一帧一般定义为Fu，帧内按标准流程进行编码;

        Fc(constrained frame)：对于帧内所有CTU都进行最大depth限制的帧，编码复杂度降低的帧。

        如图：将视频帧定义为Fu和Fc两类。对于每个Fu，编码过程中按照标准中正常的流程进行编码，Fu编码结束后，记录每一个64*64CTU的最大编码深度。Fu随后的Nc个Fc帧，编码时，对于每个CTU，编码的最大CU depth为前一个Fu的对应位置CTU的最大编码深度（Fu帧编码时以存储先来）。编码过程中，NC个Fc帧之后，Nc的值会根据目标复杂度、已编码序列的复杂度和剩余未编码帧数进行动态调整。

        具体步骤：

图4、编码步骤伪代码

        变量含义：（下面叙述中，计算复杂度可以理解为计算资源）

                Nt：视频序列中，所有帧的数目；

                Nd：当前已处理的帧数；

                Nc：连续Fc帧的数目；

                Tt：对于当前视频序列，预先定义的目标计算复杂度，可以根据CPU资源、电量或者用户自定义来确定。

                Td：当前已处理的Nd帧，所消耗的计算复杂度；

                Te：对于最新的Fu帧和其随后的Nc帧Fc帧，所消耗的计算复杂度（只有Nc个Fc帧编码完成后，才会用到Te的值）；

                Tp：根据估计，计算得到的剩余的Nt-Nd帧，还剩余的计算复杂度，按照线性比例估计。公式如下：

        根据上面伪代码，初始化相关变量之后：

            S1、先编码Fu帧，按照没有优化的流程记性所有深度的CU搜索尝试，然后将每个CTU的depth存储到MaxCUD_history[n]中，Nd++；

            S2、对于之后的Nc个Fc帧，按照每个CTU的最大depth为MaxCUD_history[i]进行编码，每处理一帧Nd++；

            S3、重新获得Te、Td(=Td+Te)和Tp(=公式1）的值；

            S4、更新Nc的值：1、如果Td+Tp>Tt*1.1（预计全部帧编码完成消耗的计算复杂度多余目标），那么Nc++，使得下一个Fu帧之后，有更多的Fc帧，从而节省计算复杂度。2、如果Td+Tp<Tt*0.9（预计全部帧编码完成消耗的计算复杂度少于目标），那么Nc--，使得下一个Fu帧之后，有更少的Fc帧，从而使用更多的计算复杂度。3、否则，NC的值保持不变。

            S5、如果编码所有帧没有完成，那么从S1继续。

            PS：对于FR（帧率）的使用，是为了保证每一秒的视频序列内有一个Fu帧，避免长期编码Fc帧，使得质量下降太多。而对于当Nc达到FR是，预计使用的编码复杂度仍然大于目标复杂度时，通过使用MaxCUD_history[i]-1来作为最大CTU深度，对计算复杂度进一步控制。

实验展示：

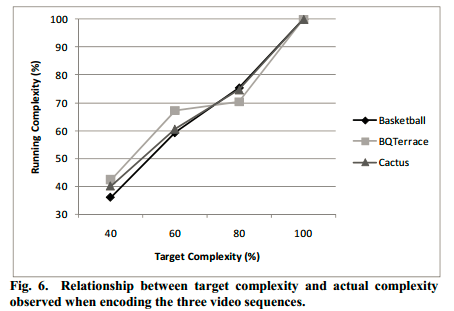
        Fig6展示的是对于三个视频序列，目标计算复杂度和实际计算复杂度，表明算法在对复杂度的控制，基本上达到了目标计算复杂度的要求。Fig7展示的是在编码一个视频序列的504帧过程中，Nc的编码过程，从图中可以看出帧率是大于25fps的。

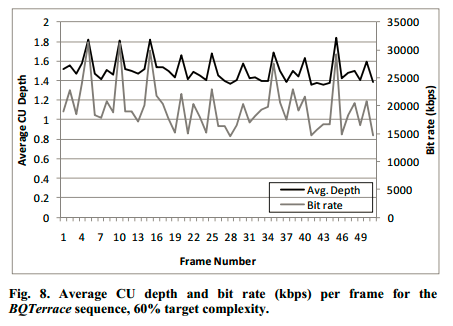
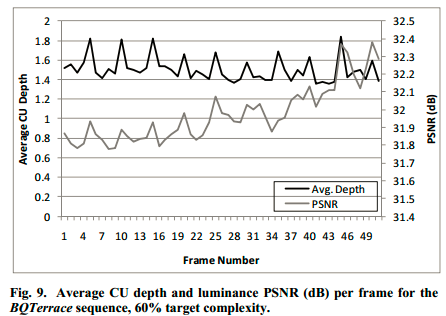
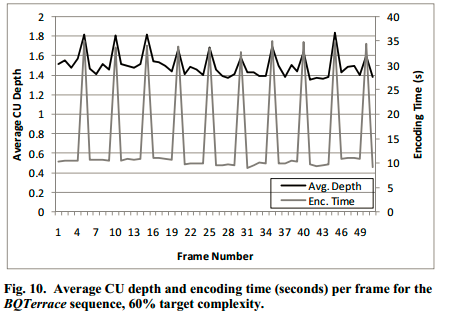
        Fig8展示的是，对于50帧测试序列，编码过程中每帧平均CU深度（黑色、左边坐标）的变化和码率（灰色、右边坐标）变化，可以看出二者都是每隔一定帧数会有一个峰值，这一帧就对应着Fu帧，而在其他帧，CU深度和码率都有一定的下降。Fig9展示的是平均CU深度和PSNR，Fig10展示的是平均CU深度和编码时间，二者与Fig8有相同的规律。

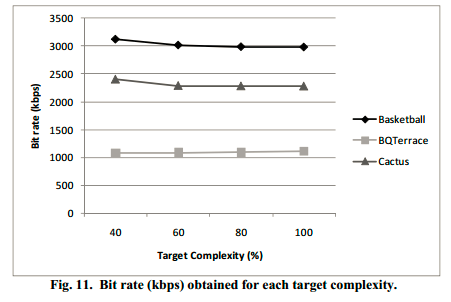
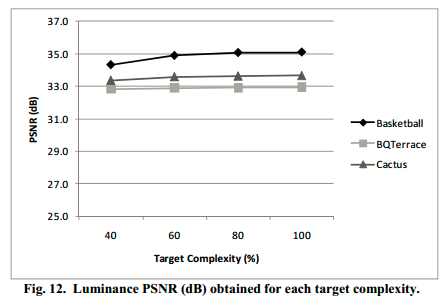
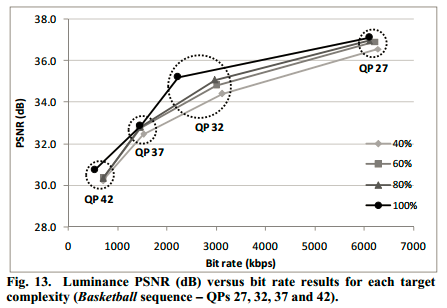
        Fig11-13，分辨从不同目标计算复杂度（不进行优化时计算复杂度的40%、60%、80%和100%）下码率、PSNR个率失真性能三个方面衡量了算法的性能，可以看出在60%、80%和100%时，码率、PSNR和率失真性能基本没有变化。只有当40%时，码率略有增加，PSNR略有降低，率失真曲线略有下降。

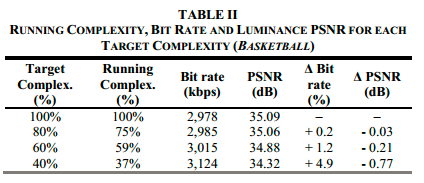
        表2-4，则分别展示了三个视频序列，在四个不同目标计算复杂度下，运行时间、码率、PSNR的表现和变化。