2019 Multi-University Training Contest 3

Contest Info
Solutions

Contest Info

[Practice Link](https://cn.vjudge.net/contest/313504#overview)

Solved	A	B	C	D	E	F	G	H	I	J	K
9/11	-	Ø	-	O	Ø	O	O	Ø	Ø	Ø	Ø

O 在比赛中通过
Ø 赛后通过
! 尝试了但是失败了
- 没有尝试

Solutions

B. Blow up the city

题意：
有一张\(DAG\)，出度为\(0\)的城市为中心城市，现在给出两个城市\(a\)、\(b\)，问破坏一个点就能使得\(a\)到达不了任意一个中心城市或者\(b\)到达不了任意一个中心城市的方案数是多少？

思路：
考虑建立反向图，然后建立一个源点\(S\)，把所有入度为\(0\)(因为是反向图)的中心城市连向它，建立支配树。
那么问题变成了，从支配中心到\(a\)的路径上有多少个点以及到\(b\)上有多少个点。
那么容斥减一下即可，注意要减去源点\(S\)。

D. Distribution of books

题意：
有一个序列\(a_i\)，要将其分成\(k\)段，每段至少有一个数，但是可以丢掉序列的最后面几个数，也就是说可以只取序列的前\(x(k \leq x \leq n)\)个数进行分出\(k\)段，使得每段的最大和最小。

思路：
考虑二分答案\(res\)，然后考虑\(check\)：

\(f[i]\)表示前\(i\)个数最多分出多少段
那么对于当前的\(i\)，当它能从\(j\)转移过来的时候应满足\(sum[i] - sum[j] \leq res\)，移项有：\(sum[i] - res \leq sum[j]\)
那么发现\(sum[j]\)的取值是一段连续的数，直接都进线段树维护即可。

代码：

#include <bits/stdc++.h>
using namespace std;

#define ll long long
#define INF 0x3f3f3f3f
#define N 400010
int n, k;
ll a[N], b[N]; 

void Hash(ll *b) {
	sort(b + 1, b + 1 + b[0]);
	b[0] = unique(b + 1, b + 1 + b[0]) - b - 1;
}

int get(ll x) {
	return lower_bound(b + 1, b + 1 + b[0], x) - b; 
}

struct SEG {
	struct node {
		int Max;
		node() {
			Max = -INF;
		}
		node operator + (const node &other) const {
			node res = node();
			res.Max = max(Max, other.Max);
			return res;
		}
	}t[N << 2];
	void build(int id, int l, int r) {
		t[id] = node();
		if (l == r) return;
		int mid = (l + r) >> 1;
		build(id << 1, l, mid);
		build(id << 1 | 1, mid + 1, r);
	}
	void update(int id, int l, int r, int pos, int x) {
		if (l == r) {
			t[id].Max = max(t[id].Max, x);
			return;
		}
		int mid = (l + r) >> 1;
		if (pos <= mid) update(id << 1, l, mid, pos, x);
		else update(id << 1 | 1, mid + 1, r, pos, x);
		t[id] = t[id << 1] + t[id << 1 | 1];
	}
	int query(int id, int l, int r, int ql, int qr) {
		if (ql > qr) return -INF;
		if (l >= ql && r <= qr) {
			return t[id].Max;
		}
		int mid = (l + r) >> 1;
		int res = -INF;
		if (ql <= mid) res = max(res, query(id << 1, l, mid, ql, qr));
		if (qr > mid) res = max(res, query(id << 1 | 1, mid + 1, r, ql, qr));
		return res;
	}
}seg;

bool check(ll x) {
	b[0] = 0;
	b[++b[0]] = 0;
	for (int i = 1; i <= n; ++i) {
		b[++b[0]] = a[i];
		b[++b[0]] = a[i] - x;
	}	
	Hash(b);
	seg.build(1, 1, b[0]);
	seg.update(1, 1, b[0], get(0), 0);
	for (int i = 1; i <= n; ++i) {
		int f = seg.query(1, 1, b[0], get(a[i] - x), b[0]) + 1;
		if (f >= k) return 1;
		seg.update(1, 1, b[0], get(a[i]), f);
	}
	return 0;
}

int main() {
	int T; scanf("%d", &T);
	while (T--) {
		scanf("%d", &n); scanf("%d", &k);
		for (int i = 1; i <= n; ++i) {
			scanf("%lld", a + i);
			a[i] += a[i - 1];
		}
		ll l = -2e15, r = 1e9, res = -1;
		while (r - l >= 0) {
			ll mid = (l + r) >> 1;
			if (check(mid)) {
				r = mid - 1;
				res = mid;
			} else {
				l = mid + 1;
			}
		}
		printf("%lld\n", res);
	}
	return 0;
}

E. Easy Math Problem

题意：
求：

\[\begin{eqnarray*} \sum\limits_{i = 1}^n \sum\limits_{j = 1}^n gcd(i, j)^k lcm(i, j)[gcd(i, j) \in prime] \bmod 10^9 + 7 \end{eqnarray*} \]

\(1 \leq n \leq 10^{10}, 1 \leq k \leq 100\)

思路：
考虑变换式子：

\[\begin{eqnarray*} &&\sum\limits_{i = 1}^n \sum\limits_{j = 1}^n gcd(i, j)^k lcm(i, j)[gcd(i, j) \in prime] \\ &=& \sum\limits_{d = 1}^n d^k [d \in prime] \sum\limits_{i = 1}^n \sum\limits_{j = 1}^n lcm(i, j)[gcd(i, j) = d] \\ &=& \sum\limits_{d = 1}^n d^{k}[d \in prime] \sum\limits_{i = 1}^n \sum\limits_{j = 1}^n \frac{i \cdot j}{d} [gcd(i, j) = d]\\ &=& \sum\limits_{d = 1}^n d^{k + 1} [d \in prime] \sum\limits_{i = 1}^{n/d}\sum\limits_{j = 1}^{n/d} ij[gcd(i, j) = 1] \\ &=& \sum\limits_{d = 1}^n d^{k + 1} [d \in prime] \sum\limits_{i = 1}^{n/d} i^2\varphi(i) \end{eqnarray*} \]

其中最后一步的变换用到一个结论：

\[\begin{eqnarray*} \sum\limits_{i = 1}^n \sum\limits_{j = 1}^n ij[gcd(i, j) = 1] = \sum\limits_{i = 1}^n i^2\varphi(i) \end{eqnarray*} \]

考虑第一部分的\(\sum\limits_{d = 1}^n d^{k + 1}\)的质数的\(k\)次幂和可以用\(Min25\)筛统计，其中\(Min25\)筛过程中求\(k + 1\)次方和可以用拉格朗日差值法在\(O(k)\)的时间处理出来。
那么再考虑第二部分\(S(n) = \sum\limits_{i = 1}^n i^2\varphi(i)\)的求和：
根据杜教筛的套路有:

\[\begin{eqnarray*} g(i)S(n) = \sum\limits_{i = 1}^n (f * g)(n) - \sum\limits_{i = 2}^n g(i)S(\left\lfloor \frac{n}{n} \right\rfloor) \end{eqnarray*} \]

因为：

\[\begin{eqnarray*} (f * g)(n) = \sum\limits_{d\;|\;n} f(d)g(\left\lfloor \frac{n}{d} \right\rfloor) \end{eqnarray*} \]

因为\(f(d) = d^2\varphi(d)\)，那么我们令\(g(n) = n^2\)，那么有：

\[\begin{eqnarray*} (f * g) (n)) &=& \sum\limits_{d\;|\;n} \frac{d^2\varphi(d)i^2}{d^2} \\ &=& \sum\limits_{d\;|\;n} n^2\varphi(d) \\ &=& n^2 \sum\limits_{d\;|\;n} \varphi(d) \\ &=& n^3 \end{eqnarray*} \]

并且有\(g(1) = 1\)，那么有:

\[\begin{eqnarray*} S(n) = \sum\limits_{i = 1}^n i^3 - \sum\limits_{i = 2}^n i^2S(\left\lfloor \frac{n}{i} \right\rfloor) \end{eqnarray*} \]

F. Fansblog

题意：
给出一个质数\(p(10^9 \leq p \leq 10^{14})\)，要求找到第一个小于它的另一个质数\(q\)，求：

\[\begin{eqnarray*} q! \bmod p \end{eqnarray*} \]

思路：
考虑威尔逊定理：

\[\begin{eqnarray*} (p - 1)! \equiv -1 \bmod p \end{eqnarray*} \]

并且考虑素数的分布是比较密的，那么可以直接用\(Miller\_Rabin\)暴力判断找到\(q\)，然后乘逆元倒推回去即可。

代码：

#include <bits/stdc++.h>
using namespace std;

#define ll long long
ll p;
const int C = 2307;
const int S = 10;
mt19937_64 rd(time(0));
ll gcd(ll a, ll b) {
	return b ? gcd(b, a % b) : a;
}
ll mul(ll a, ll b, ll p) {
	return (a * b - (ll)(a / (long double)p * b + 1e-3) * p + p) % p;
}
ll qmod(ll base, ll n, ll p) {
	ll res = 1;
	base %= p;
	while (n) {
		if (n & 1) {
			res = mul(res, base, p);
		}
		base = mul(base, base, p);
		n >>= 1;
	}
	return res;
}
bool check(ll a, ll n) {
	ll m = n - 1, x, y;
	int j = 0;
	while (!(m & 1)) {
		m >>= 1;
		++j;
	}
	x = qmod(a, m, n);
	for (int i = 1; i <= j; x = y, ++i) {
		y = mul(x, x, n);
		if (y == 1 && x != 1 && x != n - 1) {
			return 1;
		}
	}
	return y != 1;
}
bool miller_rabin(ll n) {
	if (n < 2) {
		return 0;
	} else if (n == 2) {
		return 1;
	} else if (! (n & 1)) {
		return 0;
	}
	for (int i = 0; i < S; ++i) {
		if (check(rd() % (n - 1) + 1, n)) {
			return 0;
		}
	}
	return 1;
}

int main() {
	int T; scanf("%d", &T);
	while (T--) {
		scanf("%lld", &p);
		ll n;
		for (ll i = p - 1; ; --i) {
			if (miller_rabin(i)) {
				n = i;
				break;
			}
		}
		ll res = p - 1;
		for (ll i = p - 1; i > n; --i) {
			res = mul(res, qmod(i, p - 2, p), p);
		}
		printf("%lld\n", res);
	}
	return 0;
}

G. Find the answer

题意：
给出一个序列\(w_i(1 \leq w_i \leq m)\)，要求对于每前\(i\)个数，删去最少个数的数，使得剩下的数的和小于等于\(m\)。

思路：
将数插入权值线段树，每次查询的时候线段树上二分即可。

代码：

#include <bits/stdc++.h>
using namespace std;

namespace IO
{
    const int S=(1<<20)+5;
    //Input Correlation
    char buf[S],*H,*T;
    inline char Get()
    {
        if(H==T) T=(H=buf)+fread(buf,1,S,stdin);
        if(H==T) return -1;return *H++;
    }
    inline int read()
    {
        int x=0,fg=1;char c=Get();
        while(!isdigit(c)&&c!='-') c=Get();
        if(c=='-') fg=-1,c=Get();
        while(isdigit(c)) x=x*10+c-'0',c=Get();
        return x*fg;
    }
    inline void reads(char *s)
    {
        char c=Get();int tot=0;
        while(c<'a'||c>'z') c=Get();
        while(c>='a'&&c<='z') s[++tot]=c,c=Get();
        s[++tot]='\0';
    }
    //Output Correlation
    char obuf[S],*oS=obuf,*oT=oS+S-1,c,qu[55];int qr;
    inline void flush(){fwrite(obuf,1,oS-obuf,stdout);oS=obuf;}
    inline void putc(char x){*oS++ =x;if(oS==oT) flush();}
    template <class I>inline void print(I x)
    {
        if(!x) putc('0');
        if(x<0) putc('-'),x=-x;
        while(x) qu[++qr]=x%10+'0',x/=10;
        while(qr) putc(qu[qr--]);
    }
    inline void prints(const char *s)
    {
        int len=strlen(s);
        for(int i=0;i<len;i++) putc(s[i]);
        putc('\n');
    }
    inline void printd(int d,double x)
    {
        long long t=(long long)floor(x);
        print(t);putc('.');x-=t;
        while(d--)
        {
            double y=x*10;x*=10;
            int c=(int)floor(y);
            putc(c+'0');x-=floor(y);
        }
    }
}
using namespace IO;

#define ll long long
#define N 200010
int n, m, a[N], b[N]; 
struct SEG {
	struct node {
		ll sum; int cnt;
		node() {
			sum = cnt = 0;
		}
		node (ll sum, int cnt) : sum(sum), cnt(cnt) {}
		node operator + (const node &other) const {
			node res = node();
			res.sum = sum + other.sum;
			res.cnt = cnt + other.cnt;
			return res;
		}
	}t[N << 2];
	void build(int id, int l, int r) {
		t[id] = node();
		if (l == r) return;
		int mid = (l + r) >> 1;
		build(id << 1, l, mid);
		build(id << 1 | 1, mid + 1, r);
	}
	void update(int id, int l, int r, int x) {
		if (l == r) {
			t[id].sum += b[l];
			++t[id].cnt;
			return;
		}
		int mid = (l + r) >> 1;
		if (x <= mid) update(id << 1, l, mid, x);
		else update(id << 1 | 1, mid + 1, r, x);
		t[id] = t[id << 1] + t[id << 1 | 1];
	}
	int query(int id, int l, int r, ll need) {
		if (need <= 0) return 0;
		if (l == r) {
			return need / b[l] + (need % b[l] != 0);
		}
		int mid = (l + r) >> 1;
		if (t[id << 1 | 1].sum >= need) 
			return query(id << 1 | 1, mid + 1, r, need);
		else
			return t[id << 1 | 1].cnt + query(id << 1, l, mid, need - t[id << 1 | 1].sum);
	}
}seg;

void Hash(int *b) {
	sort(b + 1, b + 1 + b[0]);
	b[0] = unique(b + 1, b + 1 + b[0]) - b - 1;
}

int get(int x) {
	return lower_bound(b + 1, b + 1 + b[0], x) - b;
}

int main() {
	int T; T = read();
	while (T--) {
		n = read(); m = read();
		b[0] = 0;
		for (int i = 1; i <= n; ++i) a[i] = read(), b[++b[0]] = a[i];
		Hash(b);
		seg.build(1, 1, b[0]);
		ll sum = 0;
		for (int i = 1; i <= n; ++i) {
			sum += a[i];
			print(seg.query(1, 1, b[0], sum - m));
			putc(' ');
			seg.update(1, 1, b[0], get(a[i]));
		}
		putc('\n');
	}
	flush();
	return 0;
}

H.Game

题意：
给出一个序列\(a_i\)，支持两种操作：

询问\([l, r]\)内有多少个子区间的异或和为\(0\)。
交换两个相邻的数

思路：
考虑维护前缀异或和，然后注意到每个相同的前缀异或和的个数\(x\)贡献是\(x(x - 1) / 2\)
再考虑交换，交换两个相邻的数，那么后面那个数的前缀异或不会变，前面那个数相当于在原来的基础上异或上本身和后面那个数。
那么就是一个三维的带修改莫队。
时间复杂度：\(O(n^{\frac{5}{3}})\)

I. K Subsequence

题意：
有\(n\)个数\(a_i\)，要求选出\(k\)个不相交的非递减序列，使得和最大。

思路：
考虑费用流建模：

将源点拆成\(s_1\)和\(s_2\)，中间连一条流量为\(k\)，费用为\(0\)的边。保证了只能选\(k\)个非递减序列
将每个数拆成入点\(a_{i, 0}\)和出点\(a_{i, 1}\)，中间连一条费用为\(-a_i\)，流量为\(0\)的边。
然后对于两个数\(a_i\)和\(a_j\)满足\(i > j\) 并且\(a_i \leq a_j\)，那么从\(a_{j, 1}\)向\(a_{i, 0}\)连一条流量为\(1\)，费用为\(0\)的边。
每个出点\(a_{i, 0}\)都要向\(t\)连一条流量为\(1\)，费用为\(0\)的边
然后跑最小费用最大流即可。

代码：

#include <bits/stdc++.h>
using namespace std;

#define INF 0x3f3f3f3f
#define N 4010

struct edge {
    int to, capacity, cost, rev;
    edge() {}
    edge(int to, int _capacity, int _cost, int _rev) : to(to), capacity(_capacity), cost(_cost), rev(_rev) {}
};

//时间复杂度O(F*ElogV)(F是流量, E是边数, V是顶点数)
struct Min_Cost_Max_Flow {
    int V, H[N + 5], dis[N + 5], PreV[N + 5], PreE[N + 5];
    vector<edge> G[N + 5];

    //调用前初始化
    void Init(int n) {
        V = n;
        for (int i = 0; i <= V; ++i)G[i].clear();
    }

    //加边
    void addedge(int from, int to, int cap, int cost) {
        G[from].push_back(edge(to, cap, cost, G[to].size()));
        G[to].push_back(edge(from, 0, -cost, G[from].size() - 1));
    }

    //flow是自己传进去的变量，就是最后的最大流，返回的是最小费用
    int Min_cost_max_flow(int s, int t, int f, int &flow) {
        int res = 0;
        fill(H, H + 1 + V, 0);
        while (f) {
            priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
            fill(dis, dis + 1 + V, INF);
            dis[s] = 0;
            q.push(pair<int, int>(0, s));
            while (!q.empty()) {
                pair<int, int> now = q.top();
                q.pop();
                int v = now.second;
                if (dis[v] < now.first)continue;
                for (int i = 0, sze = (int)G[v].size(); i < sze; ++i) {
                    edge &e = G[v][i];
                    if (e.capacity > 0 && dis[e.to] > dis[v] + e.cost + H[v] - H[e.to]) {
                        dis[e.to] = dis[v] + e.cost + H[v] - H[e.to];
                        PreV[e.to] = v;
                        PreE[e.to] = i;
                        q.push(pair<int, int>(dis[e.to], e.to));
                    }
                }
            }
            if (dis[t] == INF)break;
            for (int i = 0; i <= V; ++i)H[i] += dis[i];
            int d = f;
            for (int v = t; v != s; v = PreV[v])d = min(d, G[PreV[v]][PreE[v]].capacity);
            f -= d;
            flow += d;
            res += d * H[t];
            for (int v = t; v != s; v = PreV[v]) {
                edge &e = G[PreV[v]][PreE[v]];
                e.capacity -= d;
                G[v][e.rev].capacity += d;
            }
        }
        return res;
    }

    int Max_cost_max_flow(int s, int t, int f, int &flow) {
        int res = 0;
        fill(H, H + 1 + V, 0);
        while (f) {
            priority_queue<pair<int, int>> q;
            fill(dis, dis + 1 + V, -INF);
            dis[s] = 0;
            q.push(pair<int, int>(0, s));
            while (!q.empty()) {
                pair<int, int> now = q.top();
                q.pop();
                int v = now.second;
                if (dis[v] > now.first)continue;
                for (int i = 0, sze = (int)G[v].size(); i < sze; ++i) {
                    edge &e = G[v][i];
                    if (e.capacity > 0 && dis[e.to] < dis[v] + e.cost + H[v] - H[e.to]) {
                        dis[e.to] = dis[v] + e.cost + H[v] - H[e.to];
                        PreV[e.to] = v;
                        PreE[e.to] = i;
                        q.push(pair<int, int>(dis[e.to], e.to));
                    }
                }
            }
            if (dis[t] == -INF)break;
            for (int i = 0; i <= V; ++i)H[i] += dis[i];
            int d = f;
            for (int v = t; v != s; v = PreV[v])d = min(d, G[PreV[v]][PreE[v]].capacity);
            f -= d;
            flow += d;
            res += d * H[t];
            for (int v = t; v != s; v = PreV[v]) {
                edge &e = G[PreV[v]][PreE[v]];
                e.capacity -= d;
                G[v][e.rev].capacity += d;
            }
        }
        return res;
    }
} MCMF;

int n, k, s1, s2, t, a[N], flow;

int main() {
	int T; scanf("%d", &T);
	while (T--) {
		scanf("%d%d", &n, &k);
		for (int i = 1; i <= n; ++i) scanf("%d", a + i);
		s1 = 0, s2 = 1, t = 2 * n + 2;
		MCMF.Init(t);
		MCMF.addedge(s1, s2, k, 0);
		for (int i = 1; i <= n; ++i) {
			MCMF.addedge(s2, i << 1, 1, 0);
			MCMF.addedge(i << 1, i << 1 | 1, 1, -a[i]);
			MCMF.addedge(i << 1 | 1, t, 1, 0);
		}
		for (int i = 1; i <= n; ++i) {
			for (int j = 1; j < i; ++j) {
				if (a[j] <= a[i]) {
					MCMF.addedge(j << 1 | 1, i << 1, 1, 0); 
				}
			}
		}
		printf("%d\n", -MCMF.Min_cost_max_flow(s1, t, INF, flow));
	}
    return 0;
}

J. Sindar's Art Exhibition

题意：
有一棵树，每个点有一个快乐值\(f_i\)，以及代价\(y_i\)。\(Sinder\)要进行巡回展演，它刚开始带了\(w\)件作品，然后从\(s \rightarrow t\)，每次经过一个点展览后\(w\)都会减去\(y_i\)，但是在这个点获得的快乐值为\(w \cdot f_i\)。
现在保证\(w\)大于等于路径上的\(y_i\)之和，问总的快乐值是多少。

思路：
考虑样例，我们可以将路径拆分成这两部分：

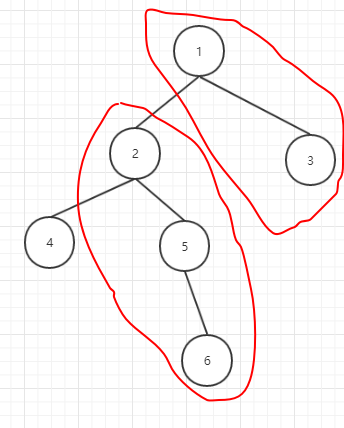
然后考虑右边部分的贡献：

用\(RF = \sum f\)表示右边部分的\(f_i\)之和
那么首先我们令贡献\(w \cdot RF\)，但是这样多算了
再令\(LY = \sum y\)表示左边部分的\(y\)之和
显然\(RF \cdot LY\)这部分多算了
还有一部分多算了，比如说点\(3\)多算了点\(1\)的\(y\)的那部分贡献，依次下去会发现是一个到根的前缀和性质，维护一下减掉就好了。
左边部分的贡献同样这么考虑。
因为有前缀和性质，所以只需要一个找\(LCA\)和一个维护前缀和的复杂度，总复杂度\(\mathcal{O}(nlogn)\)
注意这里元素的初始值\(> p\)，那么在做减法操作的时候加一个\(p\)是不够的，可以在元素读入的时候就模一下。

代码：

#include <bits/stdc++.h>
using namespace std;

#define ll long long
#define N 200010
const ll p = 1e9 + 7;
int n, q, f[N], y[N];
vector <vector<int>> G;
ll Y[N];     
void add(ll &x, ll y) {
	x += y;
	if (x >= p) x -= p;
}

int fa[N], deep[N], sze[N], son[N], top[N], in[N], fin[N], out[N], cnt;
void DFS(int u) {
	sze[u] = 1;
	for (auto v : G[u]) if (v != fa[u]) {
		fa[v] = u;
		Y[v] = (Y[u] + y[v]) % p;
		deep[v] = deep[u] + 1;
		DFS(v);
		sze[u] += sze[v];
		if (!son[u] || sze[u] > sze[son[u]]) {
			son[u] = v;
		}
	}
}

void gettop(int u, int tp) {
	top[u] = tp;
	in[u] = ++cnt;
	fin[cnt] = u;
	if (!son[u]) {
		out[u] = cnt;
		return;
	}
	gettop(son[u], tp);
	for (auto v : G[u]) if (v != fa[u] && v != son[u]) {
		gettop(v, v);
	}
	out[u] = cnt;
}

int querylca(int u, int v) {
	while (top[u] != top[v]) {
		if (deep[top[u]] < deep[top[v]]) {
			swap(u, v);
		}
		u = fa[top[u]];
	}
	if (deep[u] > deep[v]) swap(u, v);
	return u;
}

struct SEG {
	struct node {
		ll F, Fy[2], lazy[3];     
		node() {
			F = Fy[0] = Fy[1] = 0;
			lazy[0] = lazy[1] = lazy[2] = 0;
		}
		void up(ll F, ll Fy0, ll Fy1) { 
			add(this->F, F);
			add(Fy[0], Fy0);
			add(Fy[1], Fy1);
			add(lazy[0], F);
			add(lazy[1], Fy0);
			add(lazy[2], Fy1);
		}
	}t[N << 2], S, T, lca; 
	void build(int id, int l, int r) {
		t[id] = node();
		if (l == r) {
			return;
		}
		int mid = (l + r) >> 1;
		build(id << 1, l, mid);
		build(id << 1 | 1, mid + 1, r);
	}
	void pushdown(int id) {
		t[id << 1].up(t[id].lazy[0], t[id].lazy[1], t[id].lazy[2]);
		t[id << 1 | 1].up(t[id].lazy[0], t[id].lazy[1], t[id].lazy[2]);
		t[id].lazy[0] = t[id].lazy[1] = t[id].lazy[2] = 0;
	}
	void update(int id, int l, int r, int ql, int qr, ll F, ll Fy0, ll Fy1) {
		if (l >= ql && r <= qr) {
			t[id].up(F, Fy0, Fy1);
			return;
		}
		int mid = (l + r) >> 1;
		pushdown(id);
		if (ql <= mid) update(id << 1, l, mid, ql, qr, F, Fy0, Fy1);
		if (qr > mid) update(id << 1 | 1, mid + 1, r, ql, qr, F, Fy0, Fy1);
	}
	node query(int id, int l, int r, int pos) {
		if (l == r) return t[id];
		int mid = (l + r) >> 1;
		pushdown(id);
		if (pos <= mid) return query(id << 1, l, mid, pos);
		else return query(id << 1 | 1, mid + 1, r, pos);
	}
}seg;

void init() {
	G.clear(); G.resize(n + 1);
	for (int i = 1; i <= n; ++i) son[i] = 0;
	cnt = 0;
}
int main() {
	int T; scanf("%d", &T);
	while (T--) {
		scanf("%d", &n); init(); 
		for (int i = 1; i <= n; ++i) scanf("%d", f + i), f[i] %= p;
		for (int i = 1; i <= n; ++i) scanf("%d", y + i);
		for (int i = 1, u, v; i < n; ++i) {
			scanf("%d%d", &u, &v);
			G[u].push_back(v);
			G[v].push_back(u);
		}
		Y[1] = y[1]; 
		DFS(1); 
		gettop(1, 1);
		seg.build(1, 1, n);
		for (int i = 1; i <= n; ++i) {
			seg.update(1, 1, n, in[i], out[i], f[i], Y[i] * f[i] % p, (Y[i] - y[i] + p) % p * f[i] % p);
		}
		scanf("%d", &q);
		int op, s, t, x, c, v;
		while (q--) {
			scanf("%d", &op);
			if (op == 1) {
				scanf("%d%d%d", &s, &t, &x);
				ll res = 0, Ly, Ry, F, Fy;
				int lca = querylca(s, t);
				seg.S = seg.query(1, 1, n, in[s]);
				seg.T = seg.query(1, 1, n, in[t]);
				seg.lca = seg.query(1, 1, n, in[lca]); 
				//右边下去的贡献
				F = (seg.T.F - seg.lca.F + f[lca] + p) % p;   
				Fy = (seg.T.Fy[1] + p - seg.lca.Fy[1] + 1ll * f[lca] * (Y[lca] + p - y[lca]) % p) % p;
				Ly = (Y[s] + p - Y[lca]) % p; 
				add(res, F * x % p);
				add(res, p - F * Ly % p);
				add(res, p - Fy);
				add(res, F * (Y[lca] + p - y[lca]) % p);
				
				//左边上去的贡献
				Ry = (Y[t] + p - Y[lca] + y[lca]) % p;
				F = (seg.S.F + p - seg.lca.F) % p;
				Fy = (seg.S.Fy[0] + p - seg.lca.Fy[0]) % p;
				add(res, F * Ry % p);
				add(res, Fy);
				add(res, p - (F * Y[lca] % p));
				ll remindx = (x + p - Y[s] + p - Y[t] + 2ll * Y[lca] + p - y[lca]) % p;
				add(res, F * remindx % p);
				printf("%lld\n", res);
			} else {
				scanf("%d%d", &c, &v);
				seg.update(1, 1, n, in[c], out[c], p - f[c], Y[c] * (p - f[c]) % p, (Y[c] + p - y[c]) % p * (p - f[c]) % p);
				f[c] = v % p;
				seg.update(1, 1, n, in[c], out[c], f[c], Y[c] * f[c] % p, (Y[c] + p - y[c]) % p * f[c] % p);
			}
		}
	}
	return 0;
}

K. Squrirrel

题意：
有一棵树，可以删除一条边，问选择哪个为根使得所有元素的最大深度最小？

思路：
考虑不删边的版本，那么令\(f[i][2]\)表示子树内离它距离最大是多少以及次大是多少，再考虑\(g[i]\)表示从父亲方向过来的时候的距离最大是多少，然后两次\(DFS\)转移即可。
有删边的话，\(dp\)再加一维，表示删了边还是没有删边，还要多维护一个子树内距离第三大。

代码：

#include <bits/stdc++.h>
using namespace std;

#define N 200010
#define INF 0x3f3f3f3f 
#define pii pair <int, int>
#define fi first
#define se second
int n;
vector <vector<pii>> G;
pii res;
//f表示没有删边
//g表示删了一条边
pii f[N][3];
int g[N][3], h[N][3];

int fa[N], d[N];   
void DFS(int u) {
	for (auto it : G[u]) {
		int v = it.fi, w = it.se;  
		if (v == fa[u]) continue;    
		d[v] = w;
		fa[v] = u;
		DFS(v);

		//f的转移
		if (f[v][0].fi + w > f[u][0].fi) {
			f[u][2] = f[u][1];
			f[u][1] = f[u][0];
			f[u][0] = f[v][0];
			f[u][0].fi += w;
			f[u][0].se = v; 
		} else if (f[v][0].fi + w > f[u][1].fi) {
			f[u][2] = f[u][1];
			f[u][1] = f[v][0];
			f[u][1].fi += w;
			f[u][1].se = v;
		} else if (f[v][0].fi + w > f[u][2].fi) {
			f[u][2] = f[v][0];
			f[u][2].fi += w;
			f[u][2].se = v;
		}
	}
	g[u][0] = min(f[f[u][0].se][0].fi, max(f[f[u][0].se][1].fi, g[f[u][0].se][0]) + d[f[u][0].se]);
	g[u][1] = min(f[f[u][1].se][0].fi, max(f[f[u][1].se][1].fi, g[f[u][1].se][0]) + d[f[u][1].se]);	 
}

void DFS2(int u) {
	pii tmp = pii(min(max(f[u][0].fi, h[u][1]), max(h[u][0], max(g[u][0], f[u][1].fi))), u);
//	cout << tmp.fi << " " << tmp.se << endl;
	res = min(res, tmp);
	for (auto it : G[u]) {
		int v = it.fi;
		int w = it.se; 
		if (v == fa[u]) continue;
		if (f[u][0].se == v) {
			h[v][0] = max(h[u][0], f[u][1].fi) + w; 
			h[v][1] = max(h[u][0], max(f[u][2].fi, g[u][1])) + w;
			h[v][1] = min(h[v][1], max(h[u][1], f[u][1].fi) + w); 
			h[v][1] = min(h[v][1], max(h[u][0], f[u][1].fi));     
		} else {
			h[v][0] = max(h[u][0], f[u][0].fi) + w;
			if (f[u][1].se == v) {
				h[v][1] = max(h[u][0], max(f[u][2].fi, g[u][0])) + w; 
			} else {
				h[v][1] = max(h[u][0], max(f[u][1].fi, g[u][0])) + w; 
			}
			h[v][1] = min(h[v][1], max(h[u][0], f[u][0].fi));
			h[v][1] = min(h[v][1], max(h[u][1], f[u][0].fi) + w);
		}
		DFS2(v);
	}
}
	
void init() {
	G.clear(); G.resize(n + 1);
	for (int i = 1; i <= n; ++i) {
		for (int j = 0; j < 3; ++j) {
			f[i][j] = pii(0, 0);
			g[i][j] = h[i][j] = 0;
		}
	}
}
int main() {
	int T; scanf("%d", &T);
	while (T--) {
		scanf("%d", &n); init();
		for (int i = 1, u, v, w; i < n; ++i) {
			scanf("%d%d%d", &u, &v, &w);
			G[u].push_back(pii(v, w));
			G[v].push_back(pii(u, w));
		}
		res = pii(INF, INF);
		fa[1] = 1;  
		DFS(1);
		DFS2(1);
		printf("%d %d\n", res.se, res.fi);
	}
	return 0;
}

posted @ 2019-07-30 07:55 Dup4 阅读(506) 评论(0) 编辑收藏举报

刷新页面返回顶部

Dup4.Blog