2019牛客暑期多校训练营(第一场)
Contest Info
[Practice Link](https://ac.nowcoder.com/acm/contest/881#question)
| Solved | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|
| 9/10 | O | Ø | Ø | Ø | Ø | O | - | Ø | Ø | O |
- O 在比赛中通过
- Ø 赛后通过
- ! 尝试了但是失败了
- - 没有尝试
Solutions
A.Equivalent Prefixes
题意:
定理两个序列等价,当且仅当:
- 两个序列的长度相同
- \(RMQ(u, l, r) = RMQ(v, l, r)\)
\(RMQ(w, l, r)\)的定义是\([l, r]\)区间内最小数的下标
现在给出两个序列\(a_i, b_i\),保证每个序列有\(n\)个互不相同的数,问找一下最大的\(p\),使得\(\{a_1, \cdots, a_p\}\)与\(\{b_1, \cdots, b_p\}\)是等价的。
思路:
首先相当于找一个最长前缀,他们是等价的。
显然这个具有单调性。我们可以去二分长度,然后就变成了一个判定问题。
根据定义,我们要判定的是两个序列的任意一个子区间的\(RMQ\)都相同,那么反过来考虑。
我们考虑一个数的管辖范围为管辖它左边离它最近的大于它的数之间的所有数,以及右边离他最近的大于它的数之间的所有数。
那么这个管辖范围内的任意一个子区间的\(RMQ\)都是这个数的下标。
那么也就是说,只要两个序列中,每个数的管辖范围是相同的,那么这两个序列就是等价的。
求管辖范围可以用单调栈或者笛卡尔树。
代码:
#include <bits/stdc++.h>
using namespace std;
#define N 100010
int n, a[N], b[N];
struct Cartesian_Tree {
struct node {
int id, val, fa;
int son[2];
node() {}
node (int id, int val, int fa) : id(id), val(val), fa(fa) {
son[0] = son[1] = 0;
}
}t[N];
int root, l[N], r[N];
void init() {
t[0] = node(0, 0, 0);
}
void build(int n, int *a) {
for (int i = 1; i <= n; ++i) {
t[i] = node(i, a[i], 0);
}
for (int i = 1; i <= n; ++i) {
int k = i - 1;
while (t[k].val > t[i].val) {
k = t[k].fa;
}
t[i].son[0] = t[k].son[1];
t[k].son[1] = i;
t[i].fa = k;
t[t[i].son[0]].fa = i;
}
root = t[0].son[1];
}
int DFS(int u) {
if (!u) return 0;
l[t[u].id] = DFS(t[u].son[0]);
r[t[u].id] = DFS(t[u].son[1]);
return l[t[u].id] + r[t[u].id] + 1;
}
}t[2];
bool check(int x) {
t[0].init();
t[1].init();
t[0].build(x, a);
t[1].build(x, b);
t[0].DFS(t[0].root);
t[1].DFS(t[1].root);
for (int i = 1; i <= x; ++i) {
if (t[0].l[i] != t[1].l[i] || t[0].r[i] != t[1].r[i])
return 0;
}
return 1;
}
int main() {
while (scanf("%d", &n) != EOF) {
for (int i = 1; i <= n; ++i) {
scanf("%d", a + i);
}
for (int i = 1; i <= n; ++i) {
scanf("%d", b + i);
}
int l = 1, r = n, res = -1;
while (r - l >= 0) {
int mid = (l + r) >> 1;
if (check(mid)) {
res = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
printf("%d\n", res);
}
return 0;
}
B.Integration
题意:
给出:
询问
思路:
考虑\(n = 1\)时:
有不定积分:
当\(x \rightarrow \infty\)时,就是\(\frac{\pi}{2a}\)。
那么考虑\(n > 1\)时,我们知道有积分的和等于和的积分,所以我们希望把乘积拆成加减形式,那么可以用拆项积分法,比方说:
\(n = 2\)时:
考虑:
那么有:
所以:
再推个几项,就发现规律比较明显,具体参考这里
那么有:
则:
然后转化成积分的和即可。
其实我更喜欢下面这种方法:
考虑:
那么移项有:
那么显然右边的\(\prod\)项中有一项是\(a_i^2 + x^2\),那么考虑拆出来:
那么我们令\(x = a_i \cdot i\),那么\(x^2 = -a_i^2\),显然有:
因为\(k\)是会等于\(i\)的。
那么就有:
所以:
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll P = (ll) 1e9 + 7;
#define N 1010
ll qpow(ll x, ll n) {
ll res = 1;
while (n) {
if (n & 1) {
res = res * x % P;
}
x = x * x % P;
n >>= 1;
}
return res;
}
int n;
ll arr[N];
int main() {
while (~scanf("%d", &n)) {
for (int i = 1; i <= n; ++i) {
scanf("%lld", arr + i);
}
ll ans = 0;
for (int i = 1; i <= n; ++i) {
ll tmp = 2ll * arr[i];
for (int j = 1; j <= n; ++j) {
if (i == j) {
continue;
}
tmp = tmp * (arr[j] * arr[j] % P - arr[i] * arr[i] % P + P) % P;
}
ans = (ans + qpow(tmp, P - 2)) % P;
}
printf("%lld\n", ans);
}
return 0;
}
C.Euclidean Distance
题意:
有一个\(n\)维实数域\(\mathbb{R}\)的向量\((a_1/m, a_2/m, \cdots, a_n/m)\),要求找到另一个点\(P = (p_1, p_2, \cdots, p_n)\)满足以下要求:
- \(p_1, p_2, \cdots, p_n \in \mathbb{R}\)
- \(p_1, p_2 \cdots p_n \geq 0\)
- \(p_1 + p_2 + \cdots + p_n = 1\)
并且要使得
最小。
思路:
我们改变一下限制条件,我们将第三个条件改成:
那么对于答案式子,可以作如下改变:
我们考虑要求的答案式子相当于求什么,假设所有\(p_i = 0\)(显然不符合条件,不管了,先这样),那么就相当于将\(a_i\)画在坐标轴上画成矩形,求矩形的高度的平方,如下图:
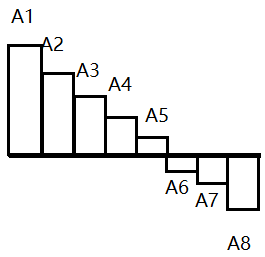
那么我们加入\(p_i\)能有什么用?
显然加入\(p_i\)能够降低一些矩形的高度,感性理解一下,肯定是尽量把高的矩形降低高度。
那么我们先降\(A_1\),使得它的高度与\(A_2\)相同。
然后呢?
然后其实可以把\(A_1, A_2\)合并起来看成一个矩形,那继续做什么?当然是降低\(A_1, A_2\)这个合并体的高度了。
然后继续做,我们发现有一步\(m\)不够了,那怎么办?
那肯定是均摊给高度相同并且最高的那个合并体,假设已经用了\(k\)了,那么还剩下\(m - k\),假设合并体的宽度(即个数)是\(i\)。
所以均摊给这其中每个独立个体的高度贡献就是
然后这个合并体的最终高度就是
然后加上剩下\(n - i\)个未变动矩形的贡献即可。
注意贡献中我们提取了一个\(\frac{1}{m^2}\),不要忘记。
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define N 10010
int n;
ll a[N], m;
struct frac{
ll x,y;
frac() {}
frac(ll x, ll y) : x(x), y(y) {}
ll gcd(ll a, ll b) {
return b ? gcd(b, a % b) : a;
}
frac operator+(const frac &u){
ll p, q;
p = x * u.y + y * u.x;
q = u.y * y;
ll d = gcd(p, q);
p /= d; q /= d;
return (frac){p, q};
}
frac operator-(const frac &u){
ll p, q;
p = x * u.y - y * u.x;
q = u.y * y;
ll d = gcd(p, q);
p /= d; q /= d;
return (frac){p, q};
}
frac operator*(const frac &u){
ll p, q;
p = u.x * x;
q = u.y * y;
ll d = gcd(p, q);
p /= d; q /= d;
return (frac){p, q};
}
frac operator/(const frac &u){
ll p, q;
p = u.y * x;
q = u.x * y;
ll d = gcd(p,q);
p /= d; q /= d;
return (frac){p,q};
}
void sqr() {
*this = (*this) * (*this);
}
void print(){
y == 1 ?
printf("%lld\n", x) :
printf("%lld/%lld\n", x, y);
}
};
int main() {
while (scanf("%d%lld", &n, &m) != EOF) {
for (int i = 1; i <= n; ++i) scanf("%lld", a + i);
sort(a + 1, a + 1 + n, [&](ll x, ll y){
return x > y;
});
ll k = m;
frac ans = frac(0, 1);
for (int i = 1; i <= n; ++i) {
if (i < n && (1ll * i * (a[i] - a[i + 1])) <= k) {
k -= 1ll * i * (a[i] - a[i + 1]);
} else {
ans = ans + frac(1ll * (i * a[i] - k) * (i * a[i] - k), 1ll * i * m * m);
for (int j = i + 1; j <= n; ++j) {
ans = ans + frac(1ll * a[j] * a[j], m * m);
}
ans.print();
break;
}
}
}
return 0;
}
D.Parity of Tuples
题意:
有\(n\)个\(m\)元组\((v_1, v_2, \cdots, v_n)\)其中\(v_i = (a_{i, 1}, \cdots, a_{i, m})\),定义\(count(x)\)为:
求\(\oplus_{x = 0}^{2^k - 1} (count(x) \cdot 3^x \bmod 10^9 + 7)\)
思路:
- 考虑一个长度为\(2\)的数组\(F\),元组\((a_1, \cdots, a_m)\)
- 对于所有元组\([m]\)的一个子集,将\(F[\oplus_{i \in S} a_i]\)加上\((-1)^{|S|}\),其中\(|S|\)表示子集的大小
- 将\(F\)做\(FWT_{xor}\),那么\(\displaystyle \frac{FWT(F)[x]}{2^m}\)就是\(count(x)\)的贡献。
为啥做一遍\(FWT_{xor}\)就可以了呢,我也不太清楚。。
根据\(qls\)的说法,\(count(x)\)后面的\(\prod\)的项需要展开成\(2^m\)项,但是因为有这样一个性质:
因为只考虑结果的奇偶性的话,\(a, b\)相同的位\(and\; x\)后一定会贡献\(0\)。
可以推广成:
因为显然可以看成:
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define N 2000010
const ll p = 1e9 + 7;
int n, m, k;
int f[N];
void DFS(vector <int> &vec, int i, int x, int p) {
if (i < (int)vec.size()) {
DFS(vec, i + 1, x, p);
DFS(vec, i + 1, x ^ vec[i], -p);
} else {
f[x] += p;
}
}
void FWT(int *x, int len) {
for (int i = 2; i <= len; i <<= 1) {
int step = i >> 1;
for (int j = 0; j < len; j += i) {
for (int k = j; k < j + step; ++k) {
ll a = x[k], b = x[k + step];
x[k] = (a + b) % p;
x[k + step] = (a - b + p) % p;
}
}
}
}
ll qmod(ll base, ll n) {
ll res = 1;
while (n) {
if (n & 1) {
res = res * base % p;
}
base = base * base % p;
n >>= 1;
}
return res;
}
int main() {
while (scanf("%d%d%d", &n, &m, &k) != EOF) {
for (int i = 0; i < 1 << k; ++i) f[i] = 0;
for (int i = 1; i <= n; ++i) {
vector <int> a(m);
for (auto &it : a) scanf("%d", &it);
DFS(a, 0, 0, 1);
}
FWT(f, 1 << k);
ll res = 0;
ll three = 1;
ll inv = qmod(qmod(2, m), p - 2);
for (int i = 0; i < 1 << k; ++i) {
res ^= 1ll * f[i] * three % p * inv % p;
three = three * 3 % p;
}
printf("%lld\n", res);
}
return 0;
}
E.ABBA
题意:
要求构造一个长度为\(2(n + m)\)的字符串,使得有一种子序列拆分拆分出\(n\)个\(AB\)以及\(m\)个\(BA\)。
问方案数。
思路:
考虑\(f[x][y]\)表示有\(x\)个\(A\)以及\(y\)个\(B\)的合法前缀的方案数,那么考虑推到\(f[x + 1][y]\),首先要满足:
- \(x + 1 \leq n + m, y \leq n + m\)
- \(x + 1 - n \leq y, y - m \leq x\),意思是\(x + 1\)个\(A\)中我全都给\(AB\)的\(A\)之后,那么剩下的\(A\)一定要可以跟前缀中的\(B\)配对,否则不合法,同理,对\(B\)的数量也如此判断。
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define N 2050
const ll p = 1e9 + 7;
int n, m;
ll f[N][N];
void add(ll &x, ll y) {
x += y;
if (x >= p) x -= p;
}
int main() {
while (scanf("%d%d", &n, &m) != EOF) {
f[0][0] = 1;
for (int i = 0; i <= n + m; ++i) {
for (int j = 0; j <= n + m; ++j) {
if ((i + 1) <= n || (i + 1 - n) <= j) {
add(f[i + 1][j], f[i][j]);
}
if ((j + 1) <= m || (j + 1 - m) <= i) {
add(f[i][j + 1], f[i][j]);
}
}
}
printf("%lld\n", f[n + m][n + m]);
for (int i = 0; i <= n + m + 10; ++i) {
for (int j = 0; j <= n + m + 10; ++j) {
f[i][j] = 0;
}
}
}
return 0;
}
F.Random Point in Triangle
题意:
给出三个点\(A, B, C\),询问在三角形中随机选取一个点,然后会构成三个三角形\(S_{PAB}, S_{PBC}, S_{PCA}\),问:
思路:
答案是\(\displaystyle \frac{11}{2}\)倍三角形的面积,,不知道为啥。
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node {
ll x, y;
void input() {
scanf("%lld %lld", &x, &y);
}
ll operator ^ (const node &other) const {
return x * other.y - y * other.x;
}
node operator - (const node &other) const {
return {x - other.x, y - other.y};
}
}p[5];
int main() {
while (~scanf("%lld %lld", &p[1].x, &p[1].y)) {
p[2].input();
p[3].input();
ll ans = abs((p[1] - p[2]) ^ (p[1] - p[3]));
ans *= 11;
printf("%lld\n", ans);
}
return 0;
}
H.XOR
题意:
有一个序列\(a_i\),询问:
思路:
考虑期望的线性性,我们可以单独计算一个数在多少个集合中出现过。
首先我们对整个序列求一个线性基\(R\),那么剩下的\(n - r\)个数,每个数出现的方案数是\(2^{n - r - 1}\)种。
因为考虑剩下的\(n - r\)个数,假设我先确定谁一定要选,那么剩下的\(n - r - 1\)个数中我不管怎么取,基\(R\)中都有一种组合方式能组合出它们的异或和。
并且是唯一组合的,因为是基中是线性无关的。
再考虑\(R\)中的每一个数的贡献。
首先我们知道,我们知道了一个序列\(a_i\)的线性基的大小是\(r\),那么一个数要想有贡献,它的贡献必定是\(2^{n - r - 1}\)种。
那么有一种显然的做法就是,枚举基\(R\)中的每一个数\(R_i\),去掉这个数,剩下的数做线性基\(B\),如果\(R_i\)还能插入到\(B\)中,说明\(R_i\)不属于线性基\(B\)构成的张成中,也就是说\(B\)中没有一种组合能够组合出\(R_i\),
那么此时\(R_i\)的方案数为\(0\),否则方案数就是\(2^{n - r - 1}\)。
有一种小优化是,先对剩下的\(n - r\)个数做一个线性基\(B\),然后枚举\(R_i\)的时候,只要往\(B\)中插入\(R_j(j \neq i)\)即可。
因为这里数的大小是\(64\)位的,所以线性基的大小不会超过\(64\)
时间复杂度:\(\mathcal{O}(64n + 64^3)\)
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define N 100010
#define M 65
const ll p = 1e9 + 7;
int n;
ll a[N];
int vis[N];
void add(ll &x, ll y) {
x += y;
if (x >= p) x -= p;
}
struct LB {
ll d[M]; int id[M];
void init() {
memset(d, 0, sizeof d);
memset(id, -1, sizeof id);
}
bool insert(ll val, int _id = 1) {
for (int i = 63; i >= 0; --i) {
if (val & (1ll << i)) {
if (!d[i]) {
id[i] = _id;
d[i] = val;
break;
}
val ^= d[i];
}
}
return val > 0;
}
}A, B, BB;
int main() {
while (scanf("%d", &n) != EOF) {
for (int i = 1; i <= n; ++i) vis[i] = 0;
for (int i = 1; i <= n; ++i) {
scanf("%lld", a + i);
}
ll res = 0;
ll two = 5e8 + 4;
A.init();
int nullity = 0;
for (int i = 1; i <= n; ++i) {
if (!A.insert(a[i], i)) {
++nullity;
add(two, two);
}
}
add(res, two * nullity % p);
B.init();
for (int i = 0; i <= 63; ++i) {
if (~A.id[i]) {
vis[A.id[i]] = 1;
}
}
vector <ll> vec;
for (int i = 1; i <= n; ++i) {
if (!vis[i]) {
B.insert(a[i], i);
} else {
vec.push_back(a[i]);
}
}
int sze = (int)vec.size();
for (int i = 0; i < sze; ++i) {
BB = B;
for (int j = 0; j < sze; ++j) {
if (i != j) {
BB.insert(vec[j]);
}
}
if (!BB.insert(vec[i])) {
add(res, two);
}
}
printf("%lld\n", res);
}
return 0;
}
I.Points Division
题意:
在二维平面上有\(n\)个点\((x_i, y_i, a_i, b_i)\),要求将他们划分到集合\(A\)或者集合\(B\)中。
如果划分到集合\(A\),那么这个点的贡献就是\(a_i\),否则贡献就是\(b_i\)。
并且要满足不存在一个\((i, j)\)使得\(i \in A, j \in B, x_i \geq x_j, y_i \leq y_j\)
思路:
考虑那个限制条件,那么在平面上必然存在一条非递减的折线,使得折线左上角的点都是集合\(A\)的,右下角的点都是集合\(B\)的。
那么我们假设折线是贴着集合\(B\)上的点的,考虑\(dp[i]\)表示到了点\(i\),它的左边的点的贡献是多少。
那么有一种转移方式,就是枚举之前的一个点\(j\),使得\(x_j \leq x_k \leq x_i\):
- \(y_k \leq y_j\)都属于集合\(B\)
- \(y_k \geq y_j\)都属于集合\(A\)
的最大贡献是多少。
那么显然在转移过程中,我们先对\(x\)轴从小到大排序,再对\(y\)轴从大到小排序。
那么我们转移的时候其实枚举\(y_j\)就可以了,因为相同的\(y_j\)而\(x_j\)不同,后面的点对他们产生的贡献是一样的,所以直接他们取\(max\)然后后面加贡献就可以了。
为什么要对\(y\)轴从大到小排序,因为折线是非递减的,我们转移时要找的\(y_j \leq y_i\),所以我们强制让\(y_i\)大的先做,这样避免重复转移状态。
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define INF 0x3f3f3f3f3f3f3f3f
#define N 100010
int n, m;
ll H[N];
struct node {
ll x, y, a, b;
node() {}
void scan() {
scanf("%lld%lld%lld%lld", &x, &y, &a, &b);
H[++m] = y;
}
bool operator < (const node &other) const {
if (x != other.x) return x < other.x;
return y > other.y;
}
}a[N];
struct SEG {
struct node {
ll Max, lazy;
node() {
Max = lazy = 0;
}
void add(ll x) {
Max += x;
lazy += x;
}
node operator + (const node &other) const {
node res = node();
res.Max = max(Max, other.Max);
return res;
}
}t[N << 2];
void build(int id, int l, int r) {
t[id] = node();
if (l == r) return;
int mid = (l + r) >> 1;
build(id << 1, l, mid);
build(id << 1 | 1, mid + 1, r);
}
void pushdown(int id) {
ll &lazy = t[id].lazy;
if (!lazy) return;
t[id << 1].add(lazy);
t[id << 1 | 1].add(lazy);
lazy = 0;
}
void update(int id, int l, int r, int ql, int qr, ll x) {
if (l >= ql && r <= qr) {
t[id].add(x);
return;
}
int mid = (l + r) >> 1;
pushdown(id);
if (ql <= mid) update(id << 1, l, mid, ql, qr, x);
if (qr > mid) update(id << 1 | 1, mid + 1, r, ql, qr, x);
t[id] = t[id << 1] + t[id << 1 | 1];
}
void update2(int id, int l, int r, int pos, ll x) {
if (l == r) {
t[id].Max = max(t[id].Max, x);
return;
}
int mid = (l + r) >> 1;
pushdown(id);
if (pos <= mid) update2(id << 1, l, mid, pos, x);
else update2(id << 1 | 1, mid + 1, r, pos, x);
t[id] = t[id << 1] + t[id << 1 | 1];
}
ll query(int id, int l, int r, int ql, int qr) {
if (l >= ql && r <= qr) {
return t[id].Max;
}
int mid = (l + r) >> 1;
pushdown(id);
ll res = 0;
if (ql <= mid) res = max(res, query(id << 1, l, mid, ql, qr));
if (qr > mid) res = max(res, query(id << 1 | 1, mid + 1, r, ql, qr));
return res;
}
}seg;
int main() {
while (scanf("%d", &n) != EOF) {
m = 0;
H[++m] = -INF;
H[++m] = INF;
for (int i = 1; i <= n; ++i) {
a[i].scan();
}
sort(a + 1, a + 1 + n);
sort(H + 1, H + 1 + m);
m = unique(H + 1, H + 1 + m) - H - 1;
for (int i = 1; i <= n; ++i) {
a[i].y = lower_bound(H + 1, H + 1 + m, a[i].y) - H;
}
seg.build(1, 1, m);
for (int i = 1; i <= n; ++i) {
ll g = seg.query(1, 1, m, 1, a[i].y);
seg.update2(1, 1, m, a[i].y, g + a[i].b);
seg.update(1, 1, m, a[i].y + 1, m, a[i].b);
seg.update(1, 1, m, 1, a[i].y - 1, a[i].a);
}
printf("%lld\n", seg.t[1].Max);
}
return 0;
}
J.Fraction Comparision
题意:
判断\(\displaystyle \frac{x}{a}\)与\(\displaystyle \frac{y}{b}\)的大小关系。
- \(0 \leq x, y \leq 10^{18}\)
- \(1 \leq a, b \leq 10^9\)
思路:
- 不能用浮点数判断
- 考虑\(xb, ya\)会爆\(long\;long\),但是\(a, b\)范围却相对较小,所以可以求出\(\left\lfloor \frac{x}{a} \right\rfloor\)以及\(\left\lfloor \frac{y}{b} \right\rfloor\),这两个东西先比较,然后再用\(x \% a, y \% b\)进行交叉相乘的比较。
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll x, y, a, b;
void out(ll A, ll B) {
if (A == B) {
puts("=");
} else if (A < B) {
puts("<");
} else {
puts(">");
}
}
int main() {
while (scanf("%lld%lld%lld%lld", &x, &a, &y, &b) != EOF) {
ll A = x / a; x %= a;
ll B = y / b; y %= b;
if (A != B) {
out(A, B);
} else {
out(x * b, y * a);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号