20251014 杂题

atcoder一类常见的折半问题.

枚举子集和枚举超集可以均摊,改为枚举一半子集,一半超级.

具体地:

其中枚举子集我写的太劣了还T了

---

P7252 [JSOI2011] 棒棒糖

区间查询绝对众数.

首先直接随机化就可以过,每次随机一个数钦定他是绝对众数,正确率很高.

然后一种确定性做法是回滚莫队(不是)

log做法是:

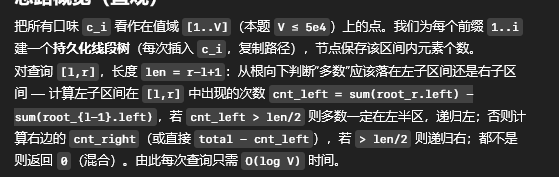
弄一个可持久化线段树,权值开,,每个版本对应下标前缀和

然后扫描线直接查即可

点击查看代码

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

// 权值主席树（persistent segment tree）实现
// 值域 [1..MAXV]
const int MAXN = 50000 + 5;
const int MAXV = 50000; // 按题意 c_i <= 5e4
// 估计节点上限： n * (log2(MAXV)+2) 安全取 20 * MAXN
const int MAXNODE = MAXN * 20;

int lc[MAXNODE], rc[MAXNODE], sumv[MAXNODE];
int roots[MAXN]; // roots[i] 表示前缀 i 的版本（i 从 0 开始，roots[0] = 0）
int tot = 1; // 0 号节点为空节点，节点编号从 1 开始

int newnode() {
    // 返回一个新节点编号（已清零）
    ++tot;
    lc[tot] = rc[tot] = 0;
    sumv[tot] = 0;
    return tot;
}

// 在 prev 版本的树上插入位置 pos，返回新版本根节点编号
int update(int prev, int l, int r, int pos) {
    int cur = newnode();
    lc[cur] = lc[prev];
    rc[cur] = rc[prev];
    sumv[cur] = sumv[prev] + 1;

    if (l == r) {
        return cur;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid) {
        lc[cur] = update(lc[prev], l, mid, pos);
    } else {
        rc[cur] = update(rc[prev], mid + 1, r, pos);
    }
    return cur;
}

// 在区间 [l,r] 中，比较两个版本 u (root_r) 和 v (root_{l-1})，长度 len，寻找多数元素的值或 0
int query_major(int u, int v, int l, int r, int len) {
    if (l == r) {
        int cnt = sumv[u] - sumv[v];
        if (cnt > len / 2) return l;
        else return 0;
    }
    int mid = (l + r) >> 1;
    int cntLeft = sumv[ lc[u] ] - sumv[ lc[v] ];
    if (cntLeft > len / 2) {
        return query_major(lc[u], lc[v], l, mid, len);
    }
    int total = sumv[u] - sumv[v];
    int cntRight = total - cntLeft;
    if (cntRight > len / 2) {
        return query_major(rc[u], rc[v], mid + 1, r, len);
    }
    return 0;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int n, m;
    if (!(cin >> n >> m)) return 0;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; ++i) cin >> a[i];

    // 初始化空节点 0 的数据（tot 从 1 开始，所以 0 作为空节点）
    lc[0] = rc[0] = 0;
    sumv[0] = 0;
    // 确保 tot >= 1 且节点 1 留作第一个 newnode() 的结果
    tot = 1; 
    lc[1] = rc[1] = 0;
    sumv[1] = 0;

    roots[0] = 0;
    // 构建每个前缀的版本
    for (int i = 1; i <= n; ++i) {
        // 在 roots[i-1] 上插入 a[i]
        roots[i] = update(roots[i-1], 1, MAXV, a[i]);
    }

    while (m--) {
        int l, r;
        cin >> l >> r;
        int len = r - l + 1;
        int ans = query_major(roots[r], roots[l - 1], 1, MAXV, len);
        cout << ans << '\n';
    }
    return 0;
}

---

P3594 [POI 2015 R3] 狼坑 Trous de loup

无敌好题.

枚举区间,再枚举减去的东西 n^3

枚举改成双指针 n^2

发现中间删除那一段是

可以用单调队列维护.

双指针过程中,右指针移动时维护单调,左指针移动时维护合法

#include<bits/stdc++.h>
using namespace std;


#define maxn 2000005
long long n, p, d, ans;
long long a[maxn], sum[maxn];
int l, h, t, q[maxn];

signed main() {
	if (!(cin >> n >> p >> d)) return 0;
	
	for(int i = 1; i <= n; ++ i) {
		if (!(cin >> a[i])) return 0;
		sum[i] = sum[i - 1] + a[i];
	}
	
	ans = d, q[t] = d, l = 1;
	
	for(int i = d + 1; i <= n; ++ i) {
		while(h <= t && sum[i] - sum[i - d] > sum[q[t]] - sum[q[t] - d]) -- t;
		q[++ t] = i;
		while(h <= t && sum[i] - sum[l - 1] - sum[q[h]] + sum[q[h] - d] > p) {
			++ l;
			while(h <= t && q[h] - d + 1 < l) ++ h;
		}
		ans = max(ans, (long long)i - l + 1);
	}
	
	cout << ans << endl;
	
	return 0;
}

是单调的