20251001-02 haosen贪心+杂题
H. 教师

看起来要状压,肯定要从n压缩。
设DP i, j, S表示考虑前i个老师,用时为j,集合S的课程已经修了。
那么转移方程就是朴素的:

因为要枚举子集和选课的缘故,要3^14左右再乘50*50,是不可接受的のだ。
考虑优化,这对于一类从S= ??...0..?? -> ??..1..??中,无论问好是什么,转移结果都一样的状压DP都能用。
我们改写一下式子

其中gain i(M\u)指的是不属于u但是属于m的那一部分。

这个式子很关键,我们发现原来的枚举子集的子集,变成了取max。
这个可以高维前缀和算。
具体地,可以先很轻松的计算
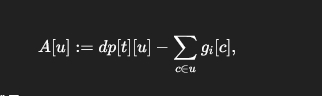
那么每个M,就需要求
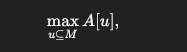
这个可以用高维前缀和求出

具体地,实现:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m, k, T;
cin >> n >> m >> k >> T;
vector<vector<ll>> v(n, vector<ll>(k + 1));
for (int i = 0; i < n; ++i)
for (int j = 0; j <= k; ++j)
cin >> v[i][j];
// 预计算基础收益 sum_base = sum v[i][0]
ll sum_base = 0;
for (int i = 0; i < n; ++i) sum_base += v[i][0];
// 老师信息
struct Teacher {
int t; // time
vector<int> courses; // 0-based course index
vector<int> to; // target ability
};
vector<Teacher> teachers(m);
for (int i = 0; i < m; ++i) {
int h, ti;
cin >> h >> ti;
teachers[i].t = ti;
teachers[i].courses.resize(h);
teachers[i].to.resize(h);
for (int j = 0; j < h; ++j) {
int l, toval;
cin >> l >> toval;
teachers[i].courses[j] = l - 1; // 0-based
teachers[i].to[j] = toval;
}
}
int FULL = 1 << n;
ll NEG = -9e18;
// 预计算每个老师对课程贡献的 sumg[mask]
vector<vector<ll>> sumg(m, vector<ll>(FULL, 0));
for (int i = 0; i < m; ++i) {
vector<ll> g(n, 0);
for (int j = 0; j < teachers[i].courses.size(); ++j) {
int c = teachers[i].courses[j];
int toval = teachers[i].to[j];
// 老师贡献 = v[c][toval] - v[c][0] (因为基础收益已经算了)
g[c] = v[c][toval] - v[c][0];
}
sumg[i][0] = 0;
for (int mask = 1; mask < FULL; ++mask) {
int lb = mask & -mask;
int bit = __builtin_ctz(lb);
sumg[i][mask] = sumg[i][mask ^ lb] + g[bit];
}
}
// dp[t][mask] = 最大收益(不包含基础收益)达到状态mask花费时间t
vector<vector<ll>> dp(T + 1, vector<ll>(FULL, NEG));
dp[0][0] = 0;
for (int i = 0; i < m; ++i) {
int ti = teachers[i].t;
// 时间倒序避免重复选同一个老师
for (int t = T - ti; t >= 0; --t) {
// A[u] = dp[t][u] - sumg[i][u]
vector<ll> A(FULL, NEG);
for (int u = 0; u < FULL; ++u) {
if (dp[t][u] > NEG/2) A[u] = dp[t][u] - sumg[i][u];
}
// SOS DP: B[M] = max_{u ⊆ M} A[u]
vector<ll> B = A;
for (int bit = 0; bit < n; ++bit) {
for (int mask = 0; mask < FULL; ++mask) {
if (mask & (1 << bit)) {
B[mask] = max(B[mask], B[mask ^ (1 << bit)]);
}
}
}
// 更新 dp[t + ti][M]
for (int M = 0; M < FULL; ++M) {
if (B[M] > NEG/2) {
ll cand = sumg[i][M] + B[M];
dp[t + ti][M] = max(dp[t + ti][M], cand);
}
}
}
}
// 输出答案:每个时间上不超过 i 的最大总收益 = dp[t][mask] + sum_base
vector<ll> ans(T + 1, 0);
for (int t = 0; t <= T; ++t) {
ll best = 0;
for (int mask = 0; mask < FULL; ++mask)
best = max(best, dp[t][mask]);
ans[t] = best + sum_base;
}
for (int i = 1; i <= T; ++i)
cout << ans[i] << "\n";
return 0;
}
C. 造桥与砍树

首先每个点点权MODk是不影响答案的。
然后考虑堆优化prim
考虑一个点p,如果要找到一个点使得与他相连是目前最优的话,把所有可以选的点插到mutiset里,然后找到y+p%k ==k最接近的y是最好的,这里也就是最小的y满足y+p%k >= k,也就是s.lower_boubd((k-p)%k)。如果找不到的话,那就找set里最小的(可以证明set里最小的一定不优于上面的,因为上面的最劣是于k最接近的,就算这样也一定比set里最小的优)
然后考虑每种点权只留一个来做生成树,因为其他点一定可以统一挂到上面的那样找到的一个最优点上去而不影响最小生成树的计算。
现在每个点权都只有一种了。
考虑堆优化prim
每个点都保证通过上面的方式找到一个最优的目标点,吧所有目标点的indx value插到堆里面,每次取最优的扩,扩展后p失去了目标点,一个新点goal,扩展他们的目标点插进堆,直到最小生成树形成即可。
初始时,我们统计每个点的点权。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
if (!(cin >> T)) return 0;
while (T--) {
int n;
ll k;
cin >> n >> k;
map<ll,int> cnt;
set<ll> s;
for (int i = 0; i < n; ++i) {
ll x; cin >> x;
ll r = x % k;
cnt[r]++;
s.insert(r);
}
ll res = 0;
for (auto &p : cnt) {
ll x = p.first;
int c = p.second;
if (c <= 1) continue;
auto it = s.lower_bound((k - x) % k);
if (it == s.end()) it = s.begin();
ll y = *it;
ll w = (x + y) % k;
res += ll(c - 1) * w;
}
priority_queue<array<ll,3>> pq;
auto add_edge = [&](ll p) {
if (s.empty()) return;
auto it = s.lower_bound((k - p) % k);
if (it == s.end()) it = s.begin();
ll y = *it;
ll w = (p + y) % k;
pq.push({ -w, y, p });
};
if (!s.empty()) {
ll start = *s.begin();
s.erase(s.begin());
add_edge(start);
}
while (!pq.empty()) {
auto cur = pq.top(); pq.pop();
ll negw = cur[0];
ll y = cur[1];
ll p = cur[2];
if (!s.count(y)) {
add_edge(p);
continue;
}
s.erase(y);
res += -negw;
add_edge(p);
add_edge(y);
}
cout << res << '\n';
}
return 0;
}

讲一下我糊的带log做法,一个点如果是mex,那么他一定在路径外,所以从小到大枚举每一个mex,那么mex等于这个点的子树,就是还没有被赋予答案,并且起点和重点都在当前枚举到的这个点的子树内或子树外的点,这是一个二维偏序。
然后是正解:

逐步扩展链(从小到大加点),然后全部加完之后,考虑一个询问路径于这条链的交集,交集是连续的,交集左侧和交集右侧的最小值一定是这个询问的mex
B. 魔塔

是那种贪心题

具体如何做的话,考虑维护一个堆,每次选择堆里最优的点往父亲转移,而不是普通的从叶子向父亲逐个反序转移,因为这样的话会漏,会导致走到点u之后就必须把儿子按某种顺序遍历一遍,这显然不对。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
// 每个块(component)维护的信息:
// tms: 块中所有怪物的攻击次数之和(即 k 的和)
// add: 块中蓝宝石的数量(每个蓝宝石使防御 +1)
// idx: 代表该块的原始节点编号(用于检测堆中元素是否过期)
struct Node {
ll tms;
ll add;
int idx;
};
// 优先队列比较器:我们希望按贪心合并的准则排序
// 如果把 a 放在 b 前比把 b 放在 a 前更优,则认为 a 更“大”
// 由不等式 add_a * tms_b > add_b * tms_a 得到比较器。
struct Cmp {
bool operator()(Node const &a, Node const &b) const {
// priority_queue 默认是最大堆;这里返回 true 表示 a < b
// 因为我们希望堆顶是“最大”的元素(即更优先合并的块),
// 所以 a < b 当且仅当 a.add * b.tms < b.add * a.tms
return a.add * b.tms < b.add * a.tms;
}
};
constexpr int MAXN = 200000 + 5;
int n;
ll X; // 勇士的攻击力
vector<int> g[MAXN]; // 树的邻接表
int parent_of[MAXN]; // 树的父节点(以 1 为根)
int dsu[MAXN]; // 并查集的父指针(合并块时使用)
Node ainfo[MAXN]; // 每个节点/块的信息
int findp(int x) {
return dsu[x] == x ? x : dsu[x] = findp(dsu[x]);
}
// 非递归构建 parent_of(以避免可能的栈溢出)
void build_parent() {
vector<int> st;
st.reserve(n);
st.push_back(1);
parent_of[1] = 0; // 根节点父亲设为 0
while (!st.empty()) {
int u = st.back(); st.pop_back();
for (int v : g[u]) {
if (v == parent_of[u]) continue;
parent_of[v] = u;
st.push_back(v);
}
}
}
// 将 tms == 0(即只有蓝宝石、没有怪物)的子块预合并到父块
// 这样可以避免这些“纯加防御”块单独存在导致排序问题
void compress_zero_tms(int u, int p) {
for (int v : g[u]) {
if (v == p) continue;
compress_zero_tms(v, u);
// 如果子节点是根(即 findp(v)==v)并且它没有怪物(tms==0),
// 则可以直接把它的 add 累加到当前节点的块上,并把并查集指向当前块
if (findp(v) == v && ainfo[v].tms == 0) {
int fu = findp(u);
ainfo[fu].add += ainfo[v].add;
dsu[v] = fu;
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
if (!(cin >> n >> X)) return 0;
for (int i = 1; i <= n; ++i) g[i].clear();
for (int i = 0; i < n - 1; ++i) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
// 初始化并查集与节点信息
for (int i = 1; i <= n; ++i) {
ainfo[i] = {0, 0, i};
dsu[i] = i;
}
ll ans = 0; // 最终答案(最大化的血量变化值)
// 读取 2..n 号点的信息(题目保证点 1 是起点)
for (int i = 2; i <= n; ++i) {
int t;
cin >> t;
if (t == 1) {
// 蓝宝石:增加防御,但不会直接改变血量
ainfo[i].add = 1;
ainfo[i].tms = 0;
} else {
// 怪物:读取 (ai, di, hi)
int ai, di, hi;
cin >> ai >> di >> hi;
// 每轮我们对怪物造成 (X - di) 伤害(题目保证 di < X)
int per = X - di;
// 怪物被击败需要 ceil(hi / per) 次我方攻击;怪物攻击次数为该值 - 1
ll k = (hi + per - 1) / per - 1;
ainfo[i].tms = k;
ainfo[i].add = 0;
// 常数部分:-k * ai(怪物每次攻击造成的血量损失),与顺序无关
ans -= k * 1ll * ai;
}
}
// 构建父节点数组
build_parent();
// 预合并没有怪物的子块到父节点(减少堆中元素,利于后续贪心)
compress_zero_tms(1, 0);
// 把每个当前的根块放入优先队列
priority_queue<Node, vector<Node>, Cmp> pq;
for (int i = 2; i <= n; ++i) {
if (findp(i) == i) pq.push(ainfo[i]);
}
// 贪心合并:每次取堆顶块 cur,把它合并到 parent(cur) 所在的块
while (!pq.empty()) {
Node cur = pq.top(); pq.pop();
int idx = cur.idx;
// 若堆中的元素已过期(代表 id 已经被合并到别的块),则跳过
if (findp(idx) != idx) continue;
// 再次校验当前信息是否与堆中一致(防止重复入堆导致的陈旧信息)
if (ainfo[idx].idx != idx || ainfo[idx].add != cur.add || ainfo[idx].tms != cur.tms) continue;
if (idx == 1) continue; // 根节点不合并到父节点
int par = parent_of[idx];
int root_par = findp(par);
// 把当前块放在父块之后,会为答案带来 parent.add * cur.tms 的增益
ans += ainfo[root_par].add * ainfo[idx].tms;
// 合并:把 cur 的 add/tms 累加到父块中,并在并查集中把 cur 指向父块
ainfo[root_par].add += ainfo[idx].add;
ainfo[root_par].tms += ainfo[idx].tms;
dsu[idx] = root_par;
// 把更新后的父块再次入堆(可能需要继续与父的父比较)
pq.push(ainfo[root_par]);
}
cout << ans << '
';
return 0;
}
https://www.luogu.com.cn/problem/AT_arc180_d


具体地,对于第一种情况,总代价是这个:
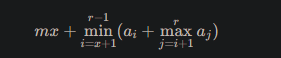
把min里面的东西设为fi,那么扫描线r每+1,可以通过维护一个值单调降(后缀max)的单调栈,用线段树更新(单点加),然后扫描线过程中区间max即可。



提到的点一定可以这样构造:
或者是一些特殊情况。
把直径对视为边,会形成一个n分图?反图就是若干个完全图团,把他们求出来即可。

很严的限制,每个点必须被覆盖一次。

树剖维护
加点的时候,先加上初始必要的边代价
统计加点对他父亲造成的奇偶性影响修改即可。

考虑起点左侧:
1001100S
最优的选择一定是反转最远的那一个之后,往回走,一旦往回走的时左面出现了新的1,就是开始的情况(再次回头)
这个感性理解一下,发现这个是最优策略,直接从左往右扫维护即可。

先考虑一个朴素DP,把字典树建出来

但是trie太大了,,但是我们发现同一层的点,除了顶到上界的那个节点,其他点本质相同,所以第一维就设为第i层即可,再加上类似数位dp的,有没有顶到上界的限制就行了。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号