20250915 NFLS数学专题 (未完结)
. B进制数与B-1倍数查询问题
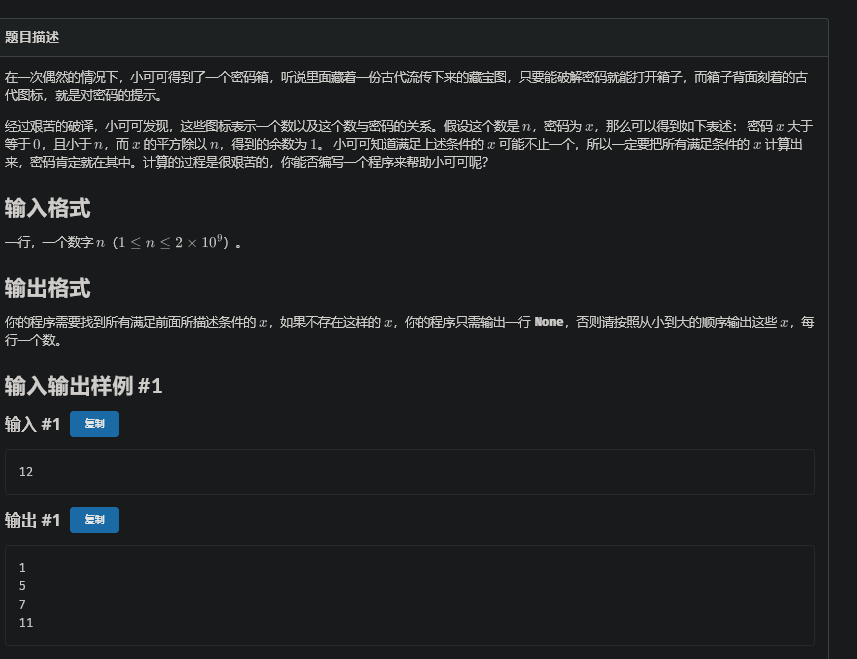
给定一个B进制数系统,其中每个数字 $ i \((\) i = 0, 1, \ldots, B-1 $)拥有 $ a[i] $ 个可用副本。要求使用这些数字组成一个最大的B进制数 $ X $,满足以下条件:
- 不能有前导零;
- 无需用完所有数字;
- $ X $ 是 $ B - 1 $ 的倍数。
现有 $ q $ 次询问,每次询问 $ X $ 在B进制下的第 $ k $ 位数字(注:最低位为第0位)。若该位不存在,则输出 \(-1\)。
输入格式
- 第一行:两个正整数 $ B \((\) 2 \leq B \leq 10^6 $)和 $ q \((\) 1 \leq q \leq 10^5 $),分别表示进制数和询问次数。
- 第二行:$ B $ 个正整数 $ a[0], a[1], \ldots, a[B-1] \((\) 1 \leq a[i] \leq 10^6 $),分别表示数字 $ 0 $ 到 $ B-1 $ 的可用个数。
- 接下来 $ q $ 行:每行一个整数 $ k \((\) 0 \leq k \leq 10^{18} $),表示一次询问的位数。
输出格式
共 $ q $ 行,依次回答每个询问:
- 若第 $ k $ 位存在,输出该位数字;
- 若该位不存在,输出 \(-1\)。
样例输入
3 3
1 1 1
0
1
2
样例输出
0
2
-1
以下是三张图片中文字内容的完整转录与整理,保留数学公式和逻辑结构:
题解
由 \((B - 1) \mid X\),
\[0 \equiv X \pmod{B - 1}
\]
\[0 \equiv \sum_{k \geq 0} v_k \cdot B^k \pmod{B - 1}
\]
\[0 \equiv \sum_{k \geq 0} v_k \cdot ((B - 1) + 1)^k \pmod{B - 1}
\]
\[0 \equiv \sum_{k \geq 0} v_k \pmod{B - 1}
\]
\[0 \equiv \sum_{0 \leq i < B} i \cdot a'_i \pmod{B - 1}
\]
其中 \(a'_i \in [0, a_i]\) 表示实际选了多少个 \(i\)。
题解
要使 \(X\) 最大,则使用的数字要尽可能多。
由于 \(a_i \geq 1\),所以我们可以求出
\[t \equiv \sum_{0 \leq i < B} i \cdot a_i \pmod{B - 1}
\]
\(t = 0\) 显然都取是最优的。当 \(t > 0\),可以构造出
\[a'_i =
\begin{cases}
a_i & \text{if } i \ne t \\
a_i - 1 & \text{if } i = t
\end{cases}
\]
表示我们只需要少选一个 \(t\) 就可以使最终和为 \(B - 1\) 的倍数。
题解
每次查询 \(X\) 的从低往高第 \(k\) 位,可以维护一个对数字个数的前缀和然后二分查找。
\[\underbrace{(B-1)\cdots(B-1)}_{a'_{B-1}\text{个}B-1} \underbrace{(B-2)\cdots(B-2)}_{a'_{B-2}\text{个}B-2} \cdots \underbrace{2\cdots2}_{a'_2\text{个}2} \underbrace{1\cdots1}_{a'_1\text{个}1} \underbrace{0\cdots0}_{a'_0\text{个}0}
\]
点击查看代码
#include <bits/stdc++.h>
using namespace std;
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int B, q;
if (!(cin >> B >> q))
return 0;
vector<int> a(B);
for (int i = 0; i < B; ++i) cin >> a[i];
int mod = B - 1;
int t = 0;
if (mod != 0) {
for (int i = 0; i < B; ++i) {
t = (t + (int)((1LL * (i % mod) * (a[i] % mod)) % mod)) % mod;
}
} else
t = 0;
vector<int> cnt = a;
if (mod != 0 && t != 0) {
if (cnt[t] > 0)
cnt[t] -= 1;
}
long long sum_nonzero = 0;
for (int i = 1; i < B; ++i) sum_nonzero += cnt[i];
if (sum_nonzero == 0) {
cnt[0] = 1;
for (int i = 1; i < B; ++i) cnt[i] = 0;
}
vector<long long> pref(B);
pref[0] = cnt[0];
for (int i = 1; i < B; ++i) pref[i] = pref[i - 1] + cnt[i];
long long total = pref[B - 1];
while (q--) {
unsigned long long k;
cin >> k;
if ((long long)k >= total) {
cout << -1 << '\n';
continue;
}
int idx = int(lower_bound(pref.begin(), pref.end(), k + 1) - pref.begin());
cout << idx << '\n';
}
return 0;
}


维护环。
在环上次数就是环长。
否则是到环上的距离
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
signed main() {
int n, k;
cin >> n >> k;
vector<int> a(n);
for (int i = 0; i < n; i++) cin >> a[i];
vector<int> num;
vector<bool> vis(n, false);
int now = 0;
int index;
while (k > 0) {
index = now % n;
if (vis[index] == true) {
break;
}
vis[index] = true;
num.push_back(index);
now = now + a[index];
k--;
}
if (k == 0) {
cout << now << endl;
return 0;
}
int pos = 0;
while (pos < (int)num.size() && num[pos] != index) pos++;
int cycle_len = (int)num.size() - pos;
int cycle_sum = 0;
for (int i = pos; i < (int)num.size(); i++) {
cycle_sum += a[num[i]];
}
now += cycle_sum * (k / cycle_len);
k = k % cycle_len;
for (int i = 0; i < k; i++) {
int idx = num[pos + i];
now += a[idx];
}
cout << now << endl;
return 0;
}


首先显然答案是所有置换环长度的lcm
置换环大小为x1,x2...xn。那么就是要找到最大的lcm(x),使得sumx = n。
并且你在知道x串时,可以简单贪心构造最小字典序。先把长为1的环扔最前面,然后往后环的长度递增放就可以了。
所以考虑吧如何固定x串

然后直接裸的背包,long double可以不用高精度
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
constexpr int maxn = 1e4+10;
int pri[maxn], pricnt = 0;
int n;
int pre[75][maxn];
long double dp[75][maxn];
int a[maxn], crilecnt = 0;
int notpri[maxn];
signed main(){
for(int i = 2;i < maxn;i++){
if(!notpri[i]){
pri[++pricnt] = i;
}
if(pricnt >= 72) break;
for(int j = 1;pri[j] * i < maxn && j <= pricnt;j++){
notpri[pri[j] * i] = true;
if(i % pri[j] == 0) break;
}
}
for(int i = 0;i < maxn;i++){
dp[0][i] = 1;
}
//dp[i][j]表示用前i个质数构成和为j的最大LCM值
for(int j = 1;j <= pricnt;j++){
for(int i = 0;i < maxn;i++){
pre[j][i] = 0;
dp[j][i] = dp[j-1][i];
}
for(int i = 0;i < maxn;i++){
for(int k = pri[j];i + k < maxn;k *= pri[j]){
if(dp[j][i + k] < dp[j-1][i] * k){
dp[j][i + k] = dp[j-1][i] * k;
pre[j][i+k] = k;
}
}
}
}
int T;
cin>>T;
while(T--){
cin>>n;
crilecnt = 0;
for(int i = pricnt;i >= 1;i--){
if(pre[i][n]){
a[++crilecnt] = pre[i][n];
n -= pre[i][n];
}
}
sort(a+1,a+crilecnt+1);
int now = 1;
for(int i = 1;i <= n;i++){
cout<<i<<" ";
now++;
}
for(int i = 1;i <= crilecnt;i++){
for(int j = now;j <= now + a[i] - 2;j++){
cout<<j+1<<" ";
}
cout<<now<<" ";
now += a[i];
}
cout<<endl;
}
return 0;
}
密码箱
x^2=kn+1
x^2-1=kn
(x+1)(x-1)=kn
令x+1=k1n1,x-1=k2n2,其中k1k2=k,n1n2=n
因此我们可以枚举n的约数中所有大于等于√n的,分别作为n1和n2代入验证,最后排序去重,可以用set
https://www.cnblogs.com/AWCXV/p/8635620.html

点击查看代码
#include <bits/stdc++.h>
using namespace std;
long long n, m;
set<long long> d;
int main() {
long long i, j;
scanf("%lld", &n);
if (n > 1)
d.insert(1);
m = sqrt(n * 1.0);
for (i = 1; i <= m; ++i) {
if (n % i == 0) {
long long x = n / i;
for (j = x; j <= n; j += x) {
if ((j - 2) % i == 0)
d.insert(j - 1);
if ((j + 2) % i == 0)
d.insert(j + 1);
}
}
}
for (auto it = d.begin(); it != d.end(); it++)
if (*it < n)
printf("%lld\n", *it);
return 0;
}

数论分块板






 浙公网安备 33010602011771号
浙公网安备 33010602011771号