20250913 NFLS 模拟赛 部分题目

简单倍增

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int main() {
	freopen("fountain.in","r",stdin);
	freopen("fountain.out","w",stdout);
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	int n, q;
	cin>>n>>q;
	vector<int> d(n + 1), c(n + 1);
	for (int i = 1; i <= n; ++i) cin >> d[i] >> c[i];
	
	vector<int> nxt(n + 1, 0);
	{
		vector<int> st;
		for (int i = n; i >= 1; --i) {
			while (!st.empty() && d[st.back()] <= d[i]) st.pop_back();
			nxt[i] = st.empty() ? 0 : st.back();
			st.push_back(i);
		}
	}
	
	const int LOG = 18;
	vector<vector<int>> up(LOG, vector<int>(n + 1, 0));
	vector<vector<ll>> sum(LOG, vector<ll>(n + 1, 0));
	for (int i = 1; i <= n; ++i) {
		up[0][i] = nxt[i];
		sum[0][i] = c[i]; 
	}
	for (int k = 1; k < LOG; ++k) {
		for (int i = 1; i <= n; ++i) {
			int mid = up[k - 1][i];
			if (mid == 0) {
				up[k][i] = 0;
				sum[k][i] = sum[k - 1][i];
			} else {
				up[k][i] = up[k - 1][mid];
				sum[k][i] = sum[k - 1][i] + sum[k - 1][mid];
			}
		}
	}
	
	while (q--) {
		int r;
		ll v;
		cin >> r >> v;
		int cur = r;
		ll acc = 0;
		
		for (int k = LOG - 1; k >= 0; --k) {
			if (cur == 0) break;
			if (up[k][cur] != 0 && acc + sum[k][cur] < v) {
				acc += sum[k][cur];
				cur = up[k][cur];
			}
		}
		
		if (acc + c[cur] >= v) {
			cout << cur << '\n';
		} else {
			cout << 0 << '\n';
		}
	}
	
	return 0;
}

---

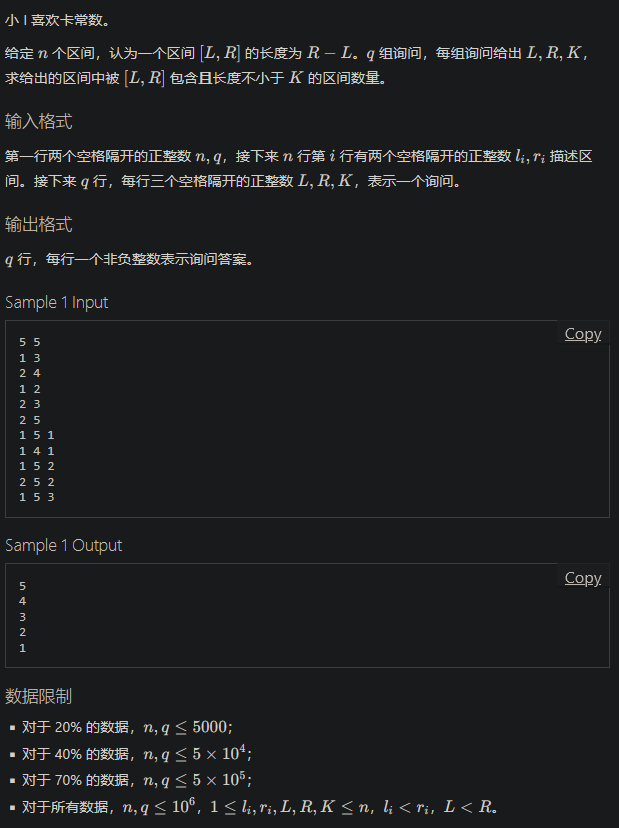
限制A和C反转一下，三维偏序板子，但是场上过不了。

我懒得写，扔一个题解

---

然后直接CDQ 是log^2的

点击查看代码

#include<bits/stdc++.h>
using namespace std;
//#define int long long 

struct Node{
	int a, b, c;
	int type, id, val;
};

char buf[200000],*p1,*p2;
#define getchar() (((p1==p2)&&(p2=(p1=buf)+fread(buf,1,200000,stdin))),*p1++)
int rd(){
	int s=0; static char c;
	while(c=getchar(),c<48);
	do s=s*10+c-48;
	while(c=getchar(),c>47);
	return s;
}

struct BIT{
	int n;
	vector<int> t;
	BIT(int _n = 0){
		init(_n);
	}
	void init(int _n){
		n = _n;
		t.assign(n+1,0);
	}
	void add(int i,int v){
		for(;i <= n;i += i & -i) t[i] += v;
	}
	int sum(int i){
		int res = 0;
		for(;i > 0;i -= i & -i)res += t[i];
		return res;
	}
};

vector<Node> e, tmp;
vector<int> ans;
BIT bit;

void cdq(int l,int r){
	if(l >= r) return;
	int mid = (l + r) >> 1;
	cdq(l,mid),cdq(mid+1,r);
	
	int i = l,j = mid+1,k = l;
	while(i <= mid && j <= r){
		if(e[i].b <= e[j].b){
			if(e[i].type == 0){
				bit.add(e[i].c,e[i].val);//1
			}
			tmp[k++] = e[i++];
		}
		else{
			if(e[j].type == 1){
				ans[e[j].id] += bit.sum(e[j].c);
			}
			tmp[k++] = e[j++];
		}
	}
	while(i <= mid){
		if(e[i].type == 0) bit.add(e[i].c,e[i].val);
		tmp[k++] = e[i++];
	}
	while(j <= r){
		if(e[j].type == 1) ans[e[j].id] += bit.sum(e[j].c);
		tmp[k++] = e[j++];
	}
	for(int p = l;p <= mid;p++){
		if(e[p].type == 0) bit.add(e[p].c,-e[p].val);
	}
	for(int p = l;p <= r;p++) e[p] = tmp[p];
}

signed main(){
	//ios::sync_with_stdio(0);
	//cin.tie(0);
	freopen("original.in","r",stdin);
	freopen("original.out","w",stdout);
	int n, q;
	n = rd(),q = rd();
	e.reserve(n+q);
	vector<int> cs;
	cs.reserve(n+q);
	
	for(int i = 0;i < n;i++){
		int l, r;
		l = rd(),r = rd();
		int len = r - l;
		Node nd;
		nd.a = -len,nd.b = r,nd.c = -l,nd.type = 0,nd.id = -1,nd.val = 1;
		e.push_back(nd);
		cs.push_back(nd.c);
	}
	
	ans.assign(q,0);
	for(int i = 0;i < q;i++){
		int l,r,k;
		l = rd(),r = rd(),k = rd();
		Node nd;
		nd.a = -k,nd.b = r,nd.c = -l;
		nd.type = 1,nd.id = i,nd.val = 0;
		e.push_back(nd);
		cs.push_back(nd.c);
	}
	sort(cs.begin(),cs.end());
	cs.erase(unique(cs.begin(),cs.end()),cs.end());
	for(auto &nd : e){
		nd.c = (int)(lower_bound(cs.begin(),cs.end(),nd.c) - cs.begin() + 1);
	}
	sort(e.begin(),e.end(),[](const Node &x,const Node &y){
		if(x.a != y.a)return x.a < y.a;
		return x.type < y.type;
	});
	
	int m = e.size();
	tmp.reserve(m);
	bit.init(cs.size()+1);
	
	cdq(0,m-1);
	for(int i = 0;i < q;i++) cout<<ans[i]<<"\n";
	return 0;
}

---

发现gcd固定一个端点后，另一个端点这个区间，最多6个本质不同GCD。

并且你考虑一个数字x，左面区间l,curx-1，右面区间curx+1,r，其中左面区间l再从curx-1到1的过程中，gcd至多跌落6次。

并且有一个结论，如果你要修改数字x，x一定是curx-1的数字的一个质因子乘以curx+1的一个质因子。

质因子本质不同6个。

所以直接枚举36个数，Pl * Pr即可，考虑如何算，对于每个数，维护集合GCDL(val,valpos)，然后遍历一下，看看这个质因子在哪个pos死掉即可。

---

和GCDR

---