20250907 NFLS 图论专题(未完结)
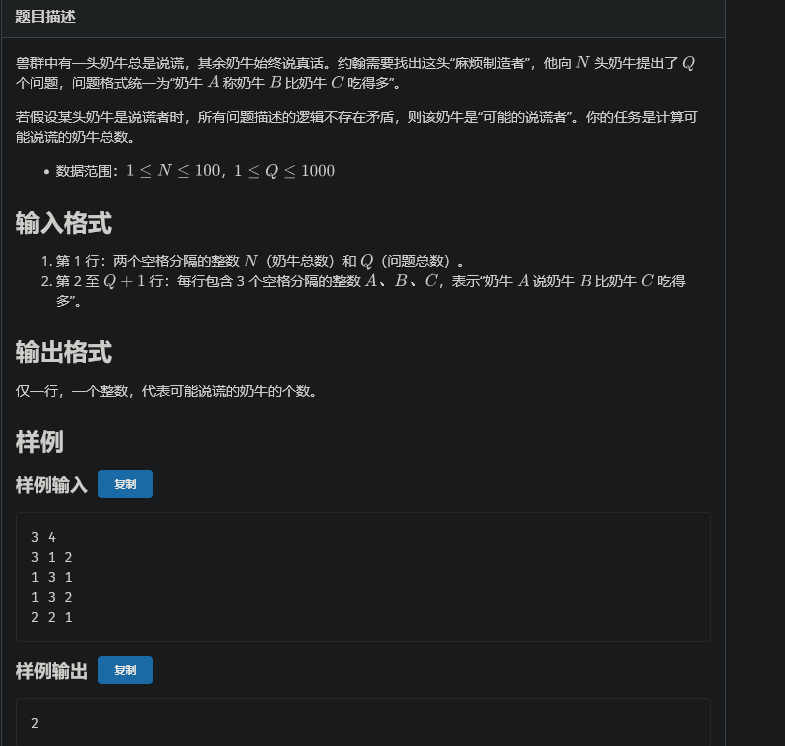
直接连边,然后枚举删除哪一个边,判断环即可
点击查看代码
#include <bits/stdc++.h>
using namespace std;
constexpr int MAXN = 110;
constexpr int MAXM = 4010;
struct Edge {
int to, next;
} e[MAXM];
int head[MAXN], cnt = 0;
void addedge(int u, int v) {
e[++cnt].to = v;
e[cnt].next = head[u];
head[u] = cnt;
}
bool del_edge[MAXN][MAXN];
int state[MAXN];
int n, m;
vector<pair<int, int>> said[MAXN];
bool dfs_cycle(int u) {
state[u] = 1;
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
if (del_edge[u][v])
continue;
if (state[v] == 1)
return true;
if (state[v] == 0) {
if (dfs_cycle(v))
return true;
}
}
state[u] = 2;
return false;
}
bool check_candidate(int x) {
memset(state, 0, sizeof(state));
memset(del_edge, 0, sizeof(del_edge));
for (auto &p : said[x]) {
del_edge[p.first][p.second] = true;
}
for (int i = 1; i <= n; ++i) {
if (state[i] == 0) {
if (dfs_cycle(i))
return false;
}
}
return true;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= m; ++i) {
int a, b, c;
cin >> a >> b >> c;
addedge(b, c);
said[a].push_back({ b, c });
}
int ans = 0;
for (int i = 1; i <= n; ++i) {
if (check_candidate(i))
++ans;
}
cout << ans << '\n';
return 0;
}

发现每个点被算通过的边次数此,所以边权是两边的点权+边权*2。起点发现可以任取
点击查看代码
#include <bits/stdc++.h>
using namespace std;
long long n;
constexpr long long maxn = 1e5 + 10;
struct DSU {
long long fa[maxn];
DSU(long long n_) {
for (long long i = 1; i <= n; i++) {
fa[i] = i;
}
}
long long find(long long x) {
if (fa[x] == x)
return x;
return fa[x] = find(fa[x]);
}
void merge(long long x, long long y) {
x = find(x), y = find(y);
fa[x] = y;
}
};
struct edge {
int u, v, w;
edge(int u_, int v_, int w_) : u(u_), v(v_), w(w_) {}
};
int main() {
ios::sync_with_stdio(0);
long long p;
cin >> n >> p;
vector<long long> c(n + 1);
long long mnc = 2147483647;
for (long long i = 1; i <= n; i++) {
cin >> c[i];
mnc = min(mnc, c[i]);
}
vector<edge> es;
for (long long i = 1; i <= p; i++) {
long long s, e, l;
cin >> s >> e >> l;
long long w = 2 * l + c[s] + c[e];
es.emplace_back(s, e, w);
}
sort(es.begin(), es.end(), [](const edge &a, const edge &b) { return a.w < b.w; });
DSU dsu(n);
long long mst = 0;
long long used = 0;
for (const auto x : es) {
if (dsu.find(x.u) != dsu.find(x.v)) {
mst += x.w;
++used;
dsu.merge(x.u, x.v);
}
}
assert(used >= n - 1);
long long ans = mst + mnc;
cout << ans << endl;
return 0;
}

先把边权定为min(K-w,0),然后跑MST,发现有可能不优秀。
直接对所有边做一次 Kruskal 得到最小的 “降权” 和;如果生成树中已有 ≥k 的边,则即为最优。
否则,两种选择取最小值:
仅用所有 <k 的边连通时需要的 “提权” 操作:k−max_edge_in_light_MST
强制“预选”一条超限边(取多余量最小者),再做 Kruskal,得到降权和
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
struct DSU {
int n;
vector<int> p, r;
DSU(int _n) : n(_n), p(n + 1), r(n + 1, 0) { iota(p.begin(), p.end(), 0); }
int find(int x) { return p[x] == x ? x : p[x] = find(p[x]); }
bool unite(int a, int b) {
a = find(a);
b = find(b);
if (a == b)
return false;
if (r[a] < r[b])
swap(a, b);
p[b] = a;
if (r[a] == r[b])
r[a]++;
return true;
}
};
struct Edge {
int u, v;
ll s;
};
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) {
int n, m;
ll k;
cin >> n >> m >> k;
vector<Edge> edges(m);
for (int i = 0; i < m; i++) {
cin >> edges[i].u >> edges[i].v >> edges[i].s;
}
auto cmpAll = [&](const Edge &a, const Edge &b) {
ll wa = max(0LL, a.s - k), wb = max(0LL, b.s - k);
if (wa != wb)
return wa < wb;
return a.s > b.s;
};
vector<Edge> allE = edges;
sort(allE.begin(), allE.end(), cmpAll);
DSU dsu1(n);
ll sum1 = 0;
bool hasHeavy1 = false;
ll maxInTree1 = 0;
int cnt1 = 0;
for (auto &e : allE) {
if (dsu1.unite(e.u, e.v)) {
cnt1++;
if (e.s > k) {
sum1 += (e.s - k);
hasHeavy1 = true;
}
maxInTree1 = max(maxInTree1, e.s);
if (cnt1 == n - 1)
break;
}
}
ll ans;
if (hasHeavy1) {
ans = sum1;
} else {
ll costA = k - maxInTree1;
ll bestExtra = LLONG_MAX;
int idxBest = -1;
for (int i = 0; i < m; i++) {
if (edges[i].s >= k) {
ll w1 = edges[i].s - k;
if (w1 < bestExtra) {
bestExtra = w1;
idxBest = i;
}
}
}
ll costB = LLONG_MAX;
if (idxBest != -1) {
DSU dsu2(n);
ll sum2 = bestExtra;
int cnt2 = 0;
dsu2.unite(edges[idxBest].u, edges[idxBest].v);
cnt2++;
for (auto &e : allE) {
if (dsu2.unite(e.u, e.v)) {
cnt2++;
if (e.s > k) {
sum2 += (e.s - k);
}
if (cnt2 == n - 1)
break;
}
}
if (cnt2 == n - 1)
costB = sum2;
}
ans = min(costA, costB);
}
cout << ans << "\n";
}
return 0;
}

直接S和T分别跑spfa即可。
注意不可达的边spfa不要走,因为如果这时候出现负环,你是无法判断负环是否可达终点的。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
constexpr int MAXN = 10000 + 10;
constexpr int MAXM = 200000 + 10;
constexpr int INF = 1e9;
struct Edge {
int to, next, val;
} e[MAXM];
int head[MAXN], cnt;
int dis[MAXN], vis[MAXN], viscnt[MAXN];
bool reachable[MAXN];
queue<int> q;
vector<int> revAdj[MAXN];
void addEdge(int u, int v, int w) {
e[++cnt].to = v;
e[cnt].val = w;
e[cnt].next = head[u];
head[u] = cnt;
revAdj[v].push_back(u);
}
void dfs(int n, int T) {
fill(reachable, reachable + n + 1, false);
queue<int> rq;
reachable[T] = true;
rq.push(T);
while (!rq.empty()) {
int u = rq.front();
rq.pop();
for (int v : revAdj[u]) {
if (!reachable[v]) {
reachable[v] = true;
rq.push(v);
}
}
}
}
bool spfa(int n, int S) {
for (int i = 0; i <= n; i++) {
dis[i] = INF;
vis[i] = 0;
viscnt[i] = 0;
}
while (!q.empty()) q.pop();
dis[S] = 0;
vis[S] = 1;
q.push(S);
while (!q.empty()) {
int u = q.front();
q.pop();
vis[u] = 0;
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
int w = e[i].val;
if (!reachable[v])
continue;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
viscnt[v] = viscnt[u] + 1;
if (viscnt[v] >= n) {
return false;
}
if (!vis[v]) {
vis[v] = 1;
q.push(v);
}
}
}
}
return true;
}
void solve() {
int n, m, Tcase;
cin >> n >> m >> Tcase;
cnt = 0;
for (int i = 0; i <= n; i++) {
head[i] = 0;
revAdj[i].clear();
}
vector<tuple<int, int, int>> edges;
edges.reserve(m);
for (int i = 0; i < m; i++) {
int u, v, w;
cin >> u >> v >> w;
edges.emplace_back(u, v, w);
}
int S, T;
cin >> S >> T;
for (auto &ed : edges) {
int u, v, w;
tie(u, v, w) = ed;
addEdge(u, v, w);
}
int ans = 0;
dfs(n, T);
if (!spfa(n, S)) {
ans++;
} else if (dis[T] <= -Tcase) {
ans++;
}
swap(S, T);
dfs(n, T);
if (!spfa(n, S)) {
ans++;
} else if (dis[T] <= -Tcase) {
ans++;
}
if (ans >= 1) {
cout << "yes" << endl;
} else {
cout << "no" << endl;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int TT;
cin >> TT;
while (TT--) {
solve();
}
return 0;
}

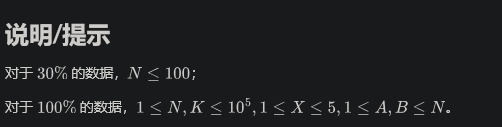
直接考虑连边

然后跑spfa,如果有负环,直接无解,但是会被卡到NM。
考虑把相等的用并查集缩点,然后跑即可
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
struct Edge {
int to, next, val;
};
constexpr int maxn = 1e6 + 10;
int n, m, cnt;
int head[maxn];
Edge e[maxn];
vector<int> fa;
int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
void merge(int a, int b) {
a = find(a);
b = find(b);
if (a != b)
fa[a] = b;
}
void addedge(int u, int v, int w) {
e[++cnt].to = v;
e[cnt].next = head[u];
e[cnt].val = w;
head[u] = cnt;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
int k;
cin >> n >> k;
fa.resize(n + 1);
for (int i = 1; i <= n; i++) fa[i] = i;
vector<array<int, 3>> rest;
for (int i = 1; i <= k; i++) {
int x, a, b;
cin >> x >> a >> b;
if (a < 1 || a > n || b < 1 || b > n) {
cout << -1 << "\n";
return 0;
}
if (x == 1) {
merge(a, b);
} else {
rest.push_back({ x, a, b });
}
}
for (auto &c : rest) {
c[1] = find(c[1]);
c[2] = find(c[2]);
if (c[1] == c[2]) {
/*
int x=c[0],a=c[1],b=c[2];
if(x==2||x==4){
cout << -1 << "\n";
return 0;
}
*/
}
}
for (auto [x, a, b] : rest) {
if (x == 2) { // a < b
addedge(a, b, 1);
} else if (x == 3) { // a >= b
addedge(b, a, 0);
} else if (x == 4) { // a > b
addedge(b, a, 1);
} else if (x == 5) { // a <= b
addedge(a, b, 0);
}
}
vector<int> d(n + 1, 1);
vector<int> inq(n + 1, 0), viscnt(n + 1, 0);
queue<int> q;
for (int i = 1; i <= n; i++)
if (find(i) == i) {
q.push(i);
inq[i] = 1;
viscnt[i] = 1;
}
while (!q.empty()) {
int u = q.front();
q.pop();
inq[u] = 0;
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].to, w = e[i].val;
if (d[v] < d[u] + w) {
d[v] = d[u] + w;
if (!inq[v]) {
q.push(v);
inq[v] = 1;
viscnt[v]++;
if (viscnt[v] > n) {
cout << -1 << "\n";
return 0;
}
}
}
}
}
int ans = 0;
for (int i = 1; i <= n; i++) ans += d[find(i)];
cout << ans << "\n";
return 0;
}

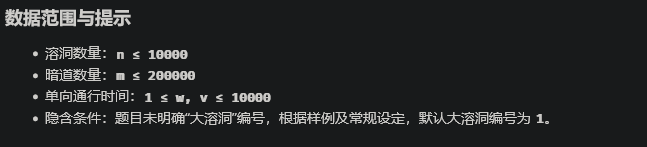
考虑从起点再往外走一条边,跑最短路,如果不再经过那一条边就是答案之一。
把起点出边编号,然后按位二进制枚举不同的集合,给边定向然后跑log次最短路。
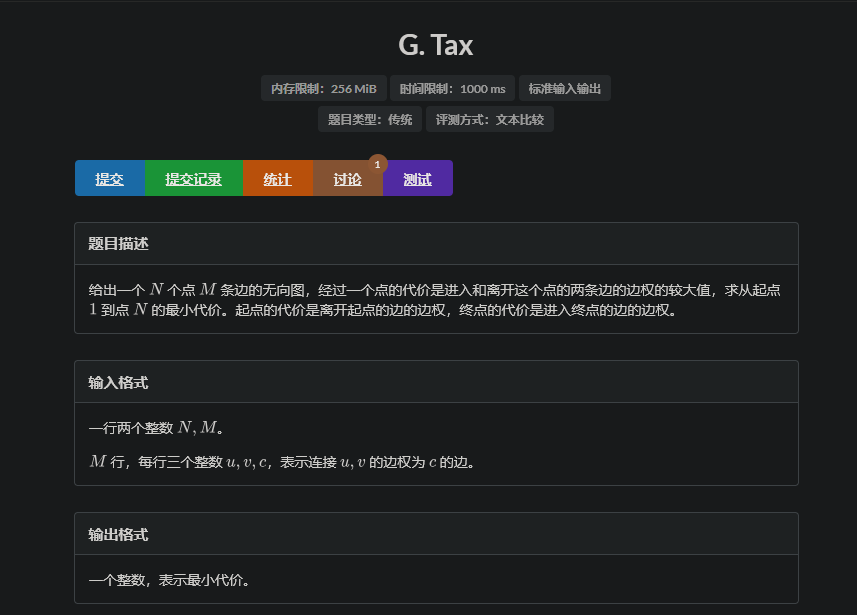

把一个边拆成两个点,考虑一个点,一个菊花(连了若干条边,我们取若干条边的靠近这个点的哪一个分成的点)。
直接n^2连边可行,但是太慢了。
考虑将边权(点权)排序,然后相邻的两个权值的点,升序边权为差值,降序边权为0,类似一个环岛,升高要补油,降低不给油,也就满足最大值的定义了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll INF = (ll)4e18;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
if (!(cin >> n >> m))
return 0;
vector<int> au(m), bu(m);
vector<ll> w(m);
for (int i = 0; i < m; ++i) {
int u, v;
ll c;
cin >> u >> v >> c;
au[i] = u;
bu[i] = v;
w[i] = c;
}
int nodes = 2 * m;
vector<vector<pair<int, ll>>> g(nodes);
vector<vector<pair<ll, int>>> out_at(n + 1);
for (int i = 0; i < m; ++i) {
int u = au[i], v = bu[i];
out_at[u].push_back({ w[i], 2 * i });
out_at[v].push_back({ w[i], 2 * i + 1 });
}
for (int v = 1; v <= n; ++v) {
if (out_at[v].empty())
continue;
auto &lst = out_at[v];
sort(lst.begin(), lst.end());
int k = (int)lst.size();
for (int j = 0; j + 1 < k; ++j) {
ll wj = lst[j].first;
ll wj1 = lst[j + 1].first;
int idj = lst[j].second;
int idj1 = lst[j + 1].second;
g[idj].push_back({ idj1, wj1 - wj });
g[idj1].push_back({ idj, 0 });
}
}
for (int i = 0; i < m; ++i) {
int a = 2 * i;
int b = 2 * i + 1;
g[a].push_back({ b, w[i] });
g[b].push_back({ a, w[i] });
}
vector<ll> dist(nodes, INF);
priority_queue<pair<ll, int>, vector<pair<ll, int>>, greater<pair<ll, int>>> pq;
for (int i = 0; i < m; ++i) {
if (au[i] == 1) {
int id = 2 * i; // 1->bu[i]
if (dist[id] > w[i]) {
dist[id] = w[i];
pq.push({ dist[id], id });
}
}
if (bu[i] == 1) {
int id = 2 * i + 1; // 1->au[i]
if (dist[id] > w[i]) {
dist[id] = w[i];
pq.push({ dist[id], id });
}
}
}
while (!pq.empty()) {
auto cur = pq.top();
pq.pop();
ll d = cur.first;
int u = cur.second;
if (d != dist[u])
continue;
for (auto &ec : g[u]) {
int v = ec.first;
ll c = ec.second;
if (dist[v] > d + c) {
dist[v] = d + c;
pq.push({ dist[v], v });
}
}
}
ll ans = INF;
for (int i = 0; i < m; ++i) {
if (bu[i] == n) {
int id = 2 * i;
if (dist[id] < INF)
ans = min(ans, dist[id] + w[i]);
}
if (au[i] == n) {
int id = 2 * i + 1;
if (dist[id] < INF)
ans = min(ans, dist[id] + w[i]);
}
}
if (ans == INF)
cout << "-1\n";
else
cout << ans << "\n";
return 0;
}

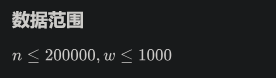

然后直接用并查集,枚举每一个权值,把w以上的边都并起来,最后累加答案,2e8,虽然computer is fast now,但是南外机子跑不过是理所当然的
点击查看代码
#include <bits/stdc++.h>
using namespace std;
struct Edge {
int u, v, w;
};
struct DSU {
int n;
vector<int> fa, sz;
DSU(int n = 0) { init(n); };
void init(int n_) {
n = n_;
fa.assign(n + 1, 0);
sz.assign(n + 1, 1);
for (int i = 1; i <= n; i++) fa[i] = i;
}
int find(int x) {
if (x == fa[x])
return x;
return fa[x] = find(fa[x]);
}
void merge(int a, int b) {
a = find(a), b = find(b);
if (a == b)
return;
if (sz[a] < sz[b])
swap(a, b);
fa[b] = a;
sz[a] += sz[b];
}
};
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
vector<Edge> edges;
int maxw = 0;
edges.reserve(n - 1);
for (int i = 1; i < n; i++) {
int u, v, w;
cin >> u >> v >> w;
edges.push_back({ u, v, w });
if (w > maxw)
maxw = w;
}
vector<int> ans(n + 1, 0);
for (int t = maxw; t > 0; t--) {
DSU dsu(n);
for (Edge &e : edges) {
if (e.w >= t)
dsu.merge(e.u, e.v);
}
for (int i = 1; i <= n; i++) {
int root = dsu.find(i);
ans[i] += dsu.sz[root] - 1;
}
}
int res = 0;
for (int i = 1; i <= n; i++) res = max(res, ans[i]);
cout << res << endl;
return 0;
}
瓶颈在于重建并查集。发现如果按边权排序,直接从大到小维护也可以。
可以通过
点击查看代码
#include <bits/stdc++.h>
using namespace std;
struct Edge {
int u, v, w;
};
struct DSU {
int n;
vector<int> fa, sz;
DSU(int n = 0) { init(n); }
void init(int n_) {
n = n_;
fa.resize(n + 1);
sz.assign(n + 1, 1);
for (int i = 1; i <= n; i++) fa[i] = i;
}
int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
void merge(int a, int b) {
a = find(a), b = find(b);
if (a == b)
return;
if (sz[a] < sz[b])
swap(a, b);
fa[b] = a;
sz[a] += sz[b];
}
};
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<Edge> edges;
edges.reserve(n - 1);
int maxw = 0;
for (int i = 1; i < n; i++) {
int u, v, w;
cin >> u >> v >> w;
edges.push_back({ u, v, w });
maxw = max(maxw, w);
}
sort(edges.begin(), edges.end(), [](auto &a, auto &b) { return a.w > b.w; });
DSU dsu(n);
vector<long long> ans(n + 1, 0);
int idx = 0;
int curw = maxw;
long long res = 0;
while (curw > 0) {
while (idx < (int)edges.size() && edges[idx].w == curw) {
dsu.merge(edges[idx].u, edges[idx].v);
idx++;
}
int nextw = (idx < (int)edges.size() ? edges[idx].w : 0);
int len = curw - nextw;
if (len > 0) {
for (int i = 1; i <= n; i++) {
int root = dsu.find(i);
ans[i] += 1LL * len * (dsu.sz[root] - 1);
res = max(res, ans[i]);
}
}
curw = nextw;
}
cout << res << "\n";
return 0;
}







 浙公网安备 33010602011771号
浙公网安备 33010602011771号