20250814 模拟赛 总结

发现合法当且仅当
空档数量<=2并且空档大小<=1
OR
空档数量<=1并且空档大小<=2

直接扫一遍即可。

---

K是奇数的话，合法点只有一个。
所以只考虑偶数的情况。

发现一个点不合法当且仅当以这个点为子树，这个树除了根的子树外的其他子树中又一棵的里面点数大于k/2，因为这时那个子树里面肯定有更优的点。所以枚举即可，可以推组合数到与k无关，但是此题不需要。

---

四元环计数板子

---

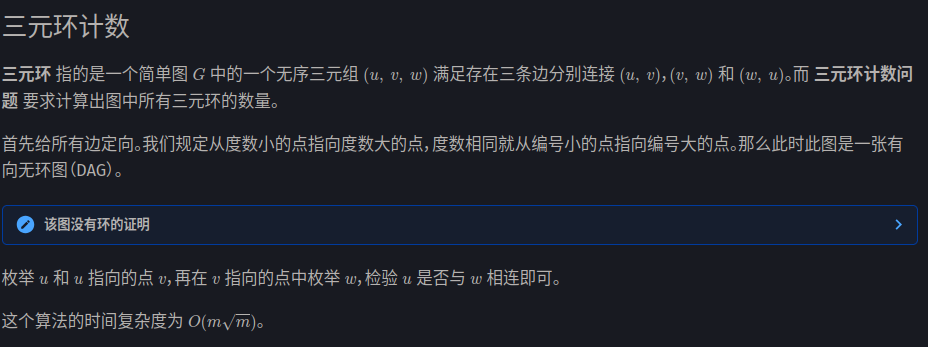
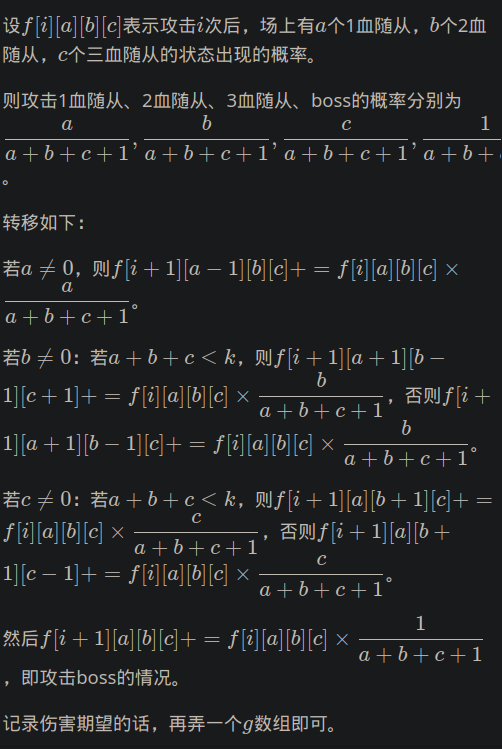
但是这样过不了，发现可以矩阵优化

状态向量要保存每一种abc组合的概率，m=3的时候有165种状态，加一个期望，就是166.

165是11选8

---

如何求矩阵，假设我们有一个转移，当前向量A和目标向量B，而已经知道Ai对Bj有 p 的贡献，那么矩阵Mji就需要加上p。

这个玩意需要程序去弄。

因为多次询问，每次都快速幂是不行的，所以二进制拆分，预处理二进制次幂即可。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int MOD = 998244353;

// 模运算的基本函数
int addmod(int a, int b){ a += b; if(a>=MOD) a-=MOD; return a; }
int submod(int a, int b){ a -= b; if(a<0) a+=MOD; return a; }
int mulmod(ll a, ll b){ return int((a*b) % MOD); }
// 快速幂（默认求逆元：a^(MOD-2)）
int modpow(int a, long long e=MOD-2){
    ll r=1, x=a;
    while(e){
        if(e&1) r = (r*x)%MOD;
        x = (x*x)%MOD;
        e >>= 1;
    }
    return int(r);
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int T, m, k;
    cin >> T >> m >> k;
    vector<long long> queries(T);
    for(int i=0;i<T;i++) cin >> queries[i];

    // 将随从数量向量（长度 m）映射为唯一整数编码
    auto encode = [&](const vector<int>& c)->int{
        int base = k+1; // 每个血量类型随从数量范围 [0,k]
        int key = 0, mul = 1;
        for(int i=0;i<m;i++){
            key += c[i]*mul;
            mul *= base;
        }
        return key;
    };

    // 初始状态：只有一个满血随从（血量 m）
    vector<int> init(m,0);
    init[m-1] = 1;

    // 状态集合映射：编码 -> 状态编号
    unordered_map<int,int> id;
    id.reserve(1000);
    vector<vector<int>> states; // 存储所有状态的随从血量分布
    queue<vector<int>> q;

    id[encode(init)] = 0;
    states.push_back(init);
    q.push(init);

    // BFS 枚举所有可达状态
    while(!q.empty()){
        auto cur = q.front(); q.pop();
        int s = 0;
        for(int x: cur) s += x; // 当前随从总数

        // 遍历打中不同血量的随从的情况
        for(int h = 1; h <= m; ++h){
            int cnt = cur[h-1]; // 剩 h 血的随从数量
            if(cnt == 0) continue;

            // 复制当前状态，修改
            vector<int> nxt = cur;
            nxt[h-1]--; // 这个随从被攻击，血量减少

            if(h > 1) nxt[h-2]++; // 血量下降到 h-1

            // 如果能召唤新随从
            if(h > 1 && s < k){
                nxt[m-1]++; // 新增一个满血随从
            }
            // h==1 时，被打死直接消失，不召唤

            // 加入状态集合
            int key = encode(nxt);
            if(id.find(key) == id.end()){
                int nid = (int)states.size();
                id[key] = nid;
                states.push_back(nxt);
                q.push(nxt);
            }
        }
    }

    int S = (int)states.size(); // 状态总数
    int N = S + 1; // 额外一维用来记录期望累加值

    // 构造转移矩阵 M（N x N）
    vector<vector<int>> M(N, vector<int>(N, 0));

    for(int idx=0; idx<S; ++idx){
        auto &cur = states[idx];
        int s = 0;
        for(int x: cur) s += x;
        int invd = modpow(s+1); // 概率分母的逆元

        // 打中 Boss 的情况：状态不变，期望累加 1
        int pb = invd; // 1 / (s+1)
        M[idx][idx] = addmod(M[idx][idx], pb); // 概率留在原状态
        M[idx][S] = addmod(M[idx][S], pb);     // 期望值 +pb

        // 打中随从的情况
        for(int h=1; h<=m; ++h){
            int cnt = cur[h-1];
            if(cnt == 0) continue;
            int p = mulmod(cnt, invd); // 概率 cnt/(s+1)

            vector<int> nxt = cur;
            nxt[h-1]--;
            if(h > 1) nxt[h-2]++;
            if(h > 1 && s < k) nxt[m-1]++;

            int to = id[encode(nxt)];
            M[idx][to] = addmod(M[idx][to], p);
        }
    }

    // 累加器的传递（始终保持累积）
    M[S][S] = 1;

    // 预处理矩阵幂 M^(2^b)
    int MAXB = 0;
    long long maxn = 0;
    for(auto &x: queries) if(x>maxn) maxn = x;
    while((1LL<<MAXB) <= maxn) MAXB++;
    if(MAXB == 0) MAXB = 1;

    // 矩阵乘法（A * B）
    auto matmul = [&](const vector<vector<int>>& A, const vector<vector<int>>& B){
        int n = (int)A.size();
        vector<vector<int>> C(n, vector<int>(n,0));
        for(int i=0;i<n;i++){
            for(int k2=0;k2<n;k2++){
                int aik = A[i][k2];
                if(aik==0) continue;
                for(int j=0;j<n;j++){
                    if(B[k2][j]==0) continue;
                    C[i][j] = (C[i][j] + (ll)aik * B[k2][j]) % MOD;
                }
            }
        }
        return C;
    };

    vector<vector<vector<int>>> Mpows;
    Mpows.push_back(M);
    for(int b=1;b<MAXB;b++){
        Mpows.push_back(matmul(Mpows[b-1], Mpows[b-1]));
    }

    // 向量乘矩阵：v' = v * mat
    auto vec_mul_mat = [&](const vector<int>& cur, const vector<vector<int>>& mat){
        int n = (int)cur.size();
        vector<int> res(n,0);
        for(int i=0;i<n;i++){
            if(cur[i]==0) continue;
            int ci = cur[i];
            for(int j=0;j<n;j++){
                if(mat[i][j]==0) continue;
                res[j] = (res[j] + (ll)ci * mat[i][j]) % MOD;
            }
        }
        return res;
    };

    // 初始向量 v0：初始状态概率为 1，累加值为 0
    vector<int> v0(N, 0);
    int start_id = id[encode(init)];
    v0[start_id] = 1;
    v0[S] = 0;

    // 处理每个询问
    for(int qi=0; qi<T; ++qi){
        long long n = queries[qi];
        vector<int> cur = v0;
        int bit = 0;
        while(n){
            if(n & 1LL){
                cur = vec_mul_mat(cur, Mpows[bit]);
            }
            n >>= 1; bit++;
        }
        // 答案是累加器位置的值
        cout << cur[S] << '\n';
    }

    return 0;
}