关于消失之物和背包与生成函数

我们知道背包的转移是

for(int j = w[i];j <= n;j++){
  f[j] = f[j] + f[j - w[i]];

而消失之物可以通过撤销来还原。

其实这玩意的本质是。

一个物品体积为 w 的 0/1 背包（要么不选，要么选它）可以用多项式表示为

具体地，当前dp状态是G(x)，考虑了物品w后会转移成F(x)。
那么是如何推出来转移是

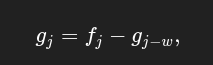
而撤销操作其实就是F(x) / (1 - x^w)。

(加号，打错了)
？

因为你考虑G(x)的k次幂的一项，乘上(1 + x^w)，1让它保持原状，而w次幂这一项使得G(x)的k-w次幂这一项的系数贡献到了k次幂，所以是fj + gj-w。