20250812 模拟赛

考虑贪心，去掉被完全覆盖的区间，然后用单调栈贪心即可。
区间排序

    把所有限制区间按 右端点降序、左端点降序 排序。

    这样能保证我们优先处理右边更靠后的区间，并且在多个区间重叠时，优先选择能“覆盖更多后续区间”的位置。

优先放置最右可用左括号

    遍历排序后的区间 (l,r)，维护一个指针 p 表示上一次选的位置。

    如果当前区间的右端点 r 在 p 之前（不重叠），就尝试在 l 位置放一个 '('（如果那里还没放过），并更新 p = l。

    这样可以用尽量靠右的 '(' 来满足区间要求，避免影响前面位置的字典序（因为 '(' < ')'，越往左放 '(' 越字典序小）。

补足剩余 '('

    放完必须的 '(' 后，如果还没达到总共 n 个 '('，就从左到右补充 '('，直到数量够。

    补的过程优先靠前位置（能进一步保证字典序最小）。

括号合法性检查

    从左到右计算括号平衡值 bal，保证任意前缀 '(' 数 ≥ ')' 数；最后必须平衡为 0。

    如果平衡性出错，或者 '(' 数不等于 n，就输出 -1。

核心思想

先用最少、最靠右的 '(' 覆盖所有区间，保证合法性；再从左往右补齐 '(' 以达到 n 个，从而使整个括号串在满足条件的情况下字典序最小。

---

我帮你把这段题解加上 \(\LaTeX\) 数学公式，排版会更清晰，而且会保留你原本的口吻。

---

提供一个 \(n\log V\) 的做法
我不想打 \(\LaTeX\)（chatgpt现在打了），我可能会说一些废话。

---

首先我们定义差分数组：

\[d_i = a_{i+1} - a_i \]

显然，你在某个区间加多少，对于区间中的 \(d\) 数组是不会变的，只会更改两个端点的差分值。

然后考虑用差分去刻画整体 \(\gcd\)。

有一个结论：

\[\gcd(a_1, a_2, \dots, a_n) = \gcd(a_1, d_1, d_2, \dots, d_{n-1}) \]

于是我们定义：

\[\text{GCD}_{\text{inside}} = \gcd(d_l, d_{l+1}, \dots, d_{r-1}) \]

\[\text{GCD}_{\text{outside}} = \gcd\bigl(\gcd(a_1, \dots, a_{l-1}),\ \gcd(a_{r+1}, \dots, a_n)\bigr) \]

对于一个区间 \([l,r]\)，你可以使得操作后的全体 GCD 达到的最大值是：

\[\gcd\bigl(\text{GCD}_{\text{inside}},\ \text{GCD}_{\text{outside}}\bigr) \]

如果直接枚举所有 \((l,r)\) 就是 \(O(n^2)\) 的做法。

---

然后考虑优化：对于一个数组，你固定右端点 \(r\)，所有不同的 \(\gcd\) 值对应的左端点其实只有 \(\log\) 级别的数量（经典结论：以某位置结尾的子段的不同 \(\gcd\) 个数是对数级的）。

于是我们可以让区间的 \(r\) 从左往右扫，对于每个 \(r\) 维护一个集合：

\[\{(\text{gcd},\ \text{leftmost\_l})\} \]

其中相同 \(\gcd\) 会合并，并保留最小的左端点 \(l\)。

当我们从 \(j-1\) 移到 \(j\) 时：

• 所有之前以 \(j-1\) 结尾的子段，都可以通过把 \(d_j\) 加到右边来延长成以 \(j\) 结尾的新子段：

\[\text{new\_gcd} = \gcd(\text{old\_gcd},\ d_j) \]

• 同时新加入单独的子段 \([j,j]\)，它的 \(\gcd = d_j\)。

把这些值合并（相同 \(\gcd\) 合并、保留最小的 \(l\)）。

因为每个 \(j\) 的集合长度均摊 \(\le O(\log V)\)，整个算法的复杂度是：

\[O(n \log V) \]

---

细节看代码

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

int main() {
    freopen("gcd.in", "r", stdin);
    freopen("gcd.out", "w", stdout);
    ios::sync_with_stdio(false);
    cin.tie(NULL);

    int T;
    if (!(cin >> T)) return 0;

    function<ll(ll, ll)> gcdll = [&](ll a, ll b) -> ll {
        return b == 0 ? a : gcdll(b, a % b);
    };

    while (T--) {
        int n;
        cin >> n;
        vector<ll> a(n + 1);
        for (int i = 1; i <= n; i++) cin >> a[i];

        if (n == 1) {
            cout << 0 << '\n';
            continue;
        }

        vector<ll> d(n);
        bool allzero = true;
        for (int i = 1; i <= n - 1; i++) {
            d[i] = llabs(a[i + 1] - a[i]);
            if (d[i] != 0) allzero = false;
        }

        if (allzero) {
            cout << 0 << '\n';
            continue;
        }

        vector<ll> pref(n + 2, 0), suf(n + 2, 0);
        for (int i = 1; i <= n; i++) pref[i] = gcdll(pref[i - 1], a[i]);
        for (int i = n; i >= 1; i--) suf[i] = gcdll(suf[i + 1], a[i]);

        ll ans = 1;
        for (int i = 1; i <= n; i++) {
            ll g_out = gcdll(pref[i - 1], suf[i + 1]);
            if (g_out > ans) ans = g_out;
        }

        vector<pair<ll, int>> cur, nxt;
        for (int j = 1; j <= n - 1; j++) {
            nxt.clear();
            nxt.push_back(make_pair(d[j], j));
            for (size_t idx = 0; idx < cur.size(); idx++) {
                ll g = gcdll(cur[idx].first, d[j]);
                int l = cur[idx].second;
                if (nxt.back().first == g) {//这里的合并保证复杂度
                    if (l < nxt.back().second) nxt.back().second = l;
                } else {
                    nxt.push_back(make_pair(g, l));
                }
            }
            for (size_t idx = 0; idx < nxt.size(); idx++) {
                ll g_in = nxt[idx].first;
                int l = nxt[idx].second;
                ll g_out = gcdll(pref[l - 1], suf[j + 2]);
                ll cand = gcdll(g_in, g_out);
                if (cand > ans) ans = cand;
            }
            cur.swap(nxt);
        }
        cout << ans << '\n';
    }

    return 0;
}

---

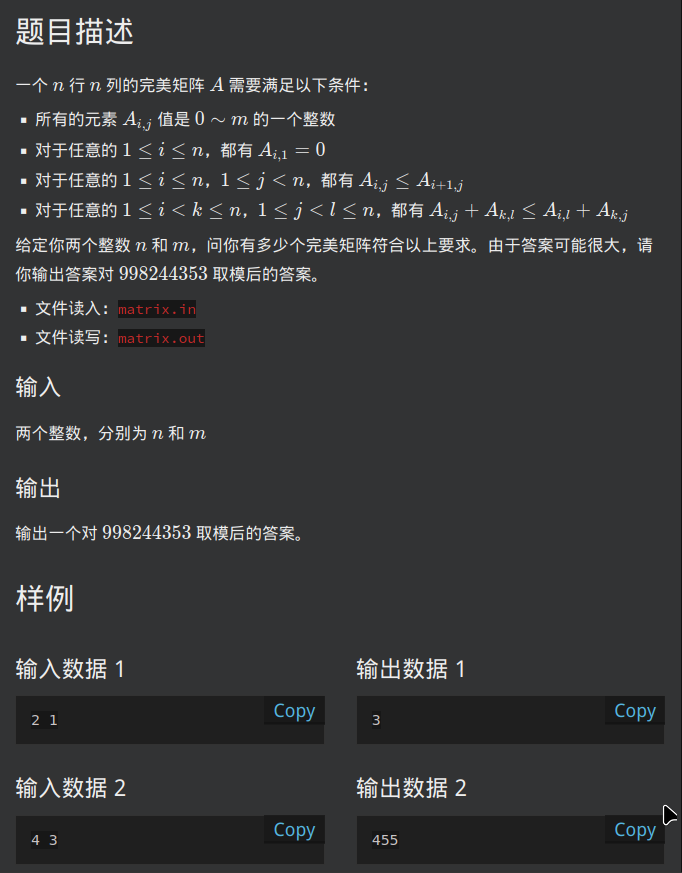
做横向差分。
限制转化为横向sum小于m，纵向单调，并且所有数字都大于1

1. 因为差分
2. 因为限制2
3. 因为限制1

---

然后考虑枚举第一行的和，那么第一行统计就是个插板，并且第一行下去每一列也是一个插板。

然后插板套插板也是插板

---

枚举每一位k
有贡献，从c这一位为1并且左面1的个数为偶数
转为原来两个数k之间的1个数％2相等。

证明不难。