20250728 线性代数专题

矩阵

就是矩阵

矩阵运算

就是矩阵的运算

行列式

1 对换行列式的两行（列），行列式变号。
2 行列式的某一行（列）中的所有元素都乘同一个数 𝑘，等于用数 𝑘 乘此行
列式。
3 把行列式的某一行（列）的各元素乘同一数然后加到另一行（列）对应元
素上去，行列式不变

求行列式

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MOD = 998244353;
const int MAXN = 2e6+5;
ll fac[MAXN], ifac[MAXN];

ll modpow(ll a, ll e=MOD-2){
	ll r=1;
	while(e){
		if(e&1) r=r*a%MOD;
		a=a*a%MOD;
		e>>=1;
	}
	return r;
}

void init(){
	fac[0]=1;
	for(int i=1;i<MAXN;i++) fac[i]=fac[i-1]*i%MOD;
	ifac[MAXN-1] = modpow(fac[MAXN-1]);
	for(int i=MAXN-2;i>=0;i--) ifac[i]=ifac[i+1]*(i+1)%MOD;
}

ll C(int x,int y){
	if(y<0 || y>x) return 0;
	return fac[x]*ifac[y]%MOD*ifac[x-y]%MOD;
}

ll det_mod(vector<vector<ll>>& A){
	ll det=1;
	int n=A.size();
	for(int i=0;i<n;i++){
		int piv=i;
		for(int j=i;j<n;j++){
			if(A[j][i]){ piv=j; break; }
		}
		if(A[piv][i]==0) return 0;
		if(piv!=i){
			swap(A[piv], A[i]);
			det = (MOD-det)%MOD;
		}
		det = det * A[i][i] % MOD;
		ll inv = modpow(A[i][i]);
		for(int j=i+1;j<n;j++){
			ll factor = A[j][i] * inv % MOD;
			for(int k=i;k<n;k++){
				A[j][k] = (A[j][k] - factor*A[i][k]) % MOD;
				if(A[j][k]<0) A[j][k]+=MOD;
			}
		}
	}
	return det;
}


int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	init();
	int T; cin>>T;
	while(T--){
		int n,m; cin>>n>>m;
		vector<int>a(m), b(m);
		for(int i=0;i<m;i++) cin>>a[i]>>b[i];
		vector<vector<ll>> E(m, vector<ll>(m));
		for(int i=0;i<m;i++)
			for(int j=0;j<m;j++)
				E[i][j] = C((n-1) + (b[j]-a[i]), n-1);
		cout << det_mod(E) << "\n";
	}
	return 0;
}

矩阵的逆

矩阵，行列式，逆矩阵线性基 LGV 引理例题总结
求解逆矩阵
如果矩阵 𝐴 可逆，则可以通过初等行变换来是的其变成单位矩阵 𝐸。而初等行
变换的作用相当于矩阵，也就意味着上文操作中若干初等行变换的作用等价于
乘上 𝐴−1。
则对单位矩阵 𝐸 进行同样的初等行变换就可以将矩阵变为 𝐴−1。
使用高斯消元法实现这一个过程：同时维护两个 𝑛 阶矩阵，其中第一个矩阵的
初值为 𝐴，第二个矩阵的初值为 𝐸。使用高斯消元法将第一个矩阵消成 𝐸，同
时对第二个矩阵进行相同的初等行变换，最终第二个矩阵的值即为 𝐴−1。

线性基

LGV引理

图上不交路径对计数

题目

新Nim游戏

现在有 𝑛 堆石子，其中第 𝑖 堆有 𝑎𝑖 个石子，现在已经游戏如下：
1 在第一个回合中，每一个人可以取走任意堆石子（可以不去，但不能全部
取完）。
2 从第二回合开始，每一个每次选择一堆石子，从中取走至少一颗石子（可
以全部取完），取走最后一颗石子的人获胜。
问先手是否存在必胜策略。如果有，他第一回合至少要取走多少颗石子。
1 ≤ 𝑛 ≤ 300，1 ≤ 𝑎𝑖 ≤ 109。

么先手有必胜策略当且仅当所有的 𝑎𝑖 异或和不为 0。

在插入线性基时，如果没成功插入，即最后x=0，那么意味着会出现异或和为0的情况，这时就要把x取走。显然，聪明的先手一定必胜，所以这题输出-1是不可能得分的了，我们只用考虑如何让取走的数量最小。

这时我们就要用到贪心思想：从大到小来试，能插入就插入，不能则取走。

那为啥这样结果最小呢？

粗略的证明一下，因为异或是不进位加法，那么，如果不是从大到小，假设a^b…=x(a≤b≤...≤x)，由于中途没有进位，因此，a^b…≤a+b+...,所以显然取走x比取走那几堆更优。

如果并不是a≤b≤...≤x呢？排个序呗。

CF895C Square Subsets

![图片](https://img2024.cnblogs.com/

blog/3478174/202507/3478174-20250728183300752-733569995.png)

题目转换为原序列 {ai} 有多少个非空子集乘积质因数分解后质数均为偶数。

发现奇偶性是满足异或性质的，奇数对应 1，偶数对应 0。考虑将原序列的每一个 ai 进行质因数分解，将分解后每个质因数的指数奇偶性二进制压位成一个整数，存到线性基中。

假设线性基中有 cnt 个元素，那么剩下的 n−cnt 个数可以用线性基的元素异或表示，可以任意取，共有 2n−cnt 种取法，注意减掉全都不取的一种就是答案。

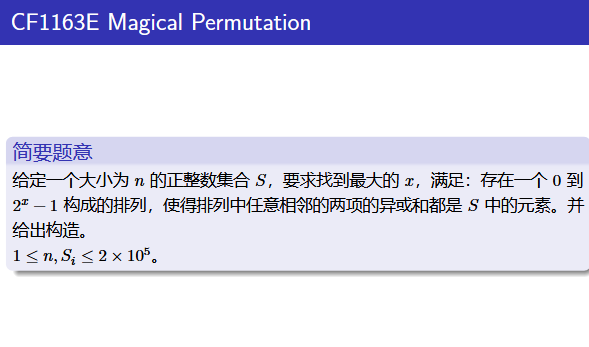
CF1163E Magical Permutation

CF348D Turtles

一张n行m列的网格图，图中的有些格子上面有障碍物，但保证(1,1)和(n,m)上面都没有障碍物。在(1,1)处有两只乌龟，都想要去(n,m)。乌龟每次都可以向下或者向右走一格，前提是格子上没有任何障碍物。要求两只乌龟在前往(n,m)的路途中不可以相遇，即除了起点和终点，他们的路径没有其他公共点。求出从起点到终点的不同路径对数。答案对109+7取模。

注：(routea,routeb)和(routeb,routea)被视为同一对路径。

显然最简起点有且只有两个，(1,2)和(2,1)，终点也同理，所以最后弄出来2*2矩阵跑LGV即可，但是我们发现这玩意本质上是反射容斥

设 F(x1,y1,x2,y2) 表示 (x1,y1)→(x2,y2) 的路径总数，那么有 ans=F(1,2,n−1,m)×F(2,1,n,m−1)−F(1,2,n,m−1)×F(2,1,n−1,m)

这个玩意是二阶矩阵行列式

但是我们发现

这样同样可以解题。

【模板】LGV 引理

和上一题类似。

Ivan and Burgers

前缀线性基。

对于普通线性基，维护pos[i]表示第i个位置上次造成影响的值的位置，每次查询l,r只需要撤销pos在l以前的即可，但是pos不是随便取的。

我们要尽可能地让pos[i]的值最大，这样才能保证我们通过上述方法构造出的线性基是[l,r]的线性基

那么如何保证pos[i]的值最大呢？

很简单，如果我们插入一个值x，它的位置为w，那么如果有一位的pos<w，那么我们就把这一位的p取出来换成x，pos换成w，然后把pos,p继续往下插入，这样构造出的线性基pos就是最大的

#include <bits/stdc++.h>
using namespace std;
constexpr int MAXN = 500000 + 10;
#define int long long

int p[31], pos[31];

void insert_basis(int valpos, int val) {
	for (int i = 30; i >= 0; --i) {
		if ((val >> i) & 1) {
			if (!p[i]) {
				p[i] = val;
				pos[i] = valpos;
				return;
			}
			if (pos[i] < valpos) {
				swap(pos[i], valpos);
				swap(p[i], val);
			}
			val ^= p[i];
		}
	}
}

int query_basis(int l) {
	int ans = 0;
	for (int i = 30; i >= 0; --i) {
		if (pos[i] >= l && (ans ^ p[i]) > ans) {
			ans ^= p[i];
		}
	}
	return ans;
}

struct Query { int l, r, idx; };

int a[MAXN];
int ans[MAXN];
int n, q;

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
	}
	cin >> q;
	
	vector<Query> qs(q);
	for (int i = 0; i < q; ++i) {
		cin >> qs[i].l >> qs[i].r;
		qs[i].idx = i;
	}
	sort(qs.begin(), qs.end(), [](auto &A, auto &B) {
		return A.r < B.r;
	});
	
	for (int i = 0; i <= 30; ++i) {
		p[i] = 0;
		pos[i] = 0;
	}
	
	int curR = 0;
	for (auto &qu : qs) {
		while (curR < qu.r) {
			++curR;
			insert_basis(curR, a[curR]);
		}
		ans[qu.idx] = query_basis(qu.l);
	}
	
	for (int i = 0; i < q; ++i) {
		cout << ans[i] << "\n";
	}
	
	return 0;
}

posted @ 2025-07-28 18:47 Dreamers_Seve 阅读(17) 评论(0) 收藏举报

刷新页面返回顶部

seve