20250726 模拟赛
想清楚再写
T1

发现一个机器可以被拆成 ai ,ai+bi,两种,直接贪心即可。
也可以考虑反悔贪心。
维护三个堆,A,A+B,-A,维护扣了A选A+B或者不扣选A,是对的。
一定要想清楚。
我场上第一步就把那玩意转化成了 a,b,c三个,直接分讨爆炸了!。
T2
题目描述
小 X 是一名老师,但是她发现学生喜欢抄袭作文。为了检验学生的抄袭程度,她将所有文章抽象成了 01 串,并发现了一个 01 串 ( S ) 可以有效地检验一篇文章的抄袭程度。具体来说,对于一个 01 串 ( T ),它的抄袭程度为 ( S ) 在 ( T ) 中的出现次数对 ( 2^{64} ) 取模的值。
小 X 最开始给出了一篇范文 ( T_0 ),保证 ( |T_0| \geq S )。
现在依次有 ( N ) 名学生依次写文章,具体他们的文章 ( T_i ) 的生成方式为:给定一个 01 串 ( D_i )(可能为空)以及一个长度为 ( k_i ) 的序列 ( a_{i,1}, a_{i,2}, \ldots, a_{i,k_i} ),则 ( T_i ) 的生成方式为:
[
T_i = T_{a_{i,1}} + T_{a_{i,2}} + \cdots + T_{a_{i,k_i}} + D_i
]
其中 ( T_{a_{i,j}} ) 表示第 ( a_{i,j} ) 篇文章(包括范文 ( T_0 ))。小 X 希望你能够告诉她每一篇文章的抄袭程度。
输入格式
从文件 string.in 中读入数据。
输入共 ( N + 3 ) 行:
- 第一行有一个数 ( N );
- 第二行有一个 01 串 ( S );
- 第三行有一个 01 串 ( T_0 );
- 接下来的每一行,输出 ( k_i + 1 ) 个数和一个字符串,分别为 ( k_i, a_{i,1}, a_{i,2}, \ldots, a_{i,k_i} ) 和 ( D_i )。
输出格式
输出到文件 string.out 中。
共 ( N ) 行,每一行一个数,表示答案。
样例 1 输入
3
01
010
2 0 1
2 1 0 101
1 2 1111
样例 1 输出
3
6
6
样例 1 解释
- ( T_1 = 0100101 )
- ( T_2 = 0100101010101 )
- ( T_3 = 010010101011111 )
样例 2
见选手目录下的 string/string2.in 与 string/string2.ans。
样例 3
见选手目录下的 string/string3.in 与 string/string3.ans。
样例 4
见选手目录下的 string/string4.in 与 string/string4.ans。
数据范围
对于所有数据,保证 ( k_i ) 是正整数。
| 测试点编号 | ( n \leq ) | ( |S|, |T_0| \leq ) | ( \sum k_i \leq ) | ( \sum |D_i| \leq ) | 特殊性质 |
|------------|--------------|-----------------------|---------------------|----------------------|-----------|
| 1 ~ 3 | 10 | 10 | 10 | 10 | 无 |
| 4 ~ 5 | ( 10^6 ) | ( 10^6 ) | ( 10^6 ) | ( 10^6 ) | A |
| 6 ~ 10 | 1000 | 1000 | 1000 | ( 2 \times 10^6 ) | B |
| 11 ~ 14 | ( 10^5 ) | ( 10^5 ) | ( 10^5 ) | ( 10^5 ) | 无 |
| 15 ~ 20 | ( 10^6 ) | ( 2 \times 10^6 ) | ( 10^6 ) | ( 2 \times 10^6 ) | 无 |
特殊性质 A:
- 所有的字符均为 0。
特殊性质 B:
- 保证 ( k_i = 1 )。
性质:
一共拼合O(n)次,这需要启发我们每次拼合都O(1)计算答案。
并且考虑T0一定长度大于S,所以我们可以O(n)预处理出来T0,考虑用字符串STR拼合T0,S在字符串STR上已经匹配了k位(k ∈ (1,|S|))的时候,在T0上接下来的贡献是多少。
然后考虑拼合,Ti = Txi + Tx2 ...... Txn,其中上面讲的就是,形如Txi + Tx2的这样的拼合一共最多1e6次,并且保证Tx2的前面一定是T0,而T0的信息我们已经预处理出来了。
问题就转化为了我们要O(1)处理X和Y拼合的问题,其中Y只会用到前|S|位,而前|S|位我们已经处理出来了在X中对于字符串S的kmp,已经匹配到了i,那么接下来在Y中会造成多少贡献。
我们只需要知道X中S能最长匹配到多少即可。
举个例子 X是ababc S是bcb,那么最长匹配长度就是2(bc),假设我们已经求出来了,就做完了。考虑如何求,我们就发现在拼合Ti的时候最后部分可以求,因为你Ti最后一部分一定是Txn + Di,而Txn的这一部分已经处理完了,只需要继续跑KMP,把Di这一段跑完即可,总复杂度是Di长度的和,所有Di的长度加起来是1e6,那就做完了。
KMP很难写,可以用哈希,多带一个log。题目描述
小 X 是一名老师,但是她发现学生喜欢抄袭作文。为了检验学生的抄袭程度,她将所有文章抽象成了 01 串,并发现了一个 01 串 ( S ) 可以有效地检验一篇文章的抄袭程度。具体来说,对于一个 01 串 ( T ),它的抄袭程度为 ( S ) 在 ( T ) 中的出现次数对 ( 2^{64} ) 取模的值。
小 X 最开始给出了一篇范文 ( T_0 ),保证 ( |T_0| \geq S )。
现在依次有 ( N ) 名学生依次写文章,具体他们的文章 ( T_i ) 的生成方式为:给定一个 01 串 ( D_i )(可能为空)以及一个长度为 ( k_i ) 的序列 ( a_{i,1}, a_{i,2}, \ldots, a_{i,k_i} ),则 ( T_i ) 的生成方式为:
[
T_i = T_{a_{i,1}} + T_{a_{i,2}} + \cdots + T_{a_{i,k_i}} + D_i
]
其中 ( T_{a_{i,j}} ) 表示第 ( a_{i,j} ) 篇文章(包括范文 ( T_0 ))。小 X 希望你能够告诉她每一篇文章的抄袭程度。
输入格式
从文件 string.in 中读入数据。
输入共 ( N + 3 ) 行:
第一行有一个数 ( N );
第二行有一个 01 串 ( S );
第三行有一个 01 串 ( T_0 );
接下来的每一行,输出 ( k_i + 1 ) 个数和一个字符串,分别为 ( k_i, a_{i,1}, a_{i,2}, \ldots, a_{i,k_i} ) 和 ( D_i )。
输出格式
输出到文件 string.out 中。
共 ( N ) 行,每一行一个数,表示答案。
样例 1 输入
3
01
010
2 0 1
2 1 0 101
1 2 1111
样例 1 输出
3
6
6
样例 1 解释
( T_1 = 0100101 )
( T_2 = 0100101010101 )
( T_3 = 010010101011111 )
样例 2
见选手目录下的 string/string2.in 与 string/string2.ans。
样例 3
见选手目录下的 string/string3.in 与 string/string3.ans。
样例 4
见选手目录下的 string/string4.in 与 string/string4.ans。
数据范围
对于所有数据,保证 ( k_i ) 是正整数。
| 测试点编号 | ( n \leq ) | ( |S|, |T_0| \leq ) | ( \sum k_i \leq ) | ( \sum |D_i| \leq ) | 特殊性质 |
|------------|--------------|-----------------------|---------------------|----------------------|-----------|
| 1 ~ 3 | 10 | 10 | 10 | 10 | 无 |
| 4 ~ 5 | ( 10^6 ) | ( 10^6 ) | ( 10^6 ) | ( 10^6 ) | A |
| 6 ~ 10 | 1000 | 1000 | 1000 | ( 2 \times 10^6 ) | B |
| 11 ~ 14 | ( 10^5 ) | ( 10^5 ) | ( 10^5 ) | ( 10^5 ) | 无 |
| 15 ~ 20 | ( 10^6 ) | ( 2 \times 10^6 ) | ( 10^6 ) | ( 2 \times 10^6 ) | 无 |
特殊性质 A:
所有的字符均为 0。
特殊性质 B:
保证 ( k_i = 1 )。
性质:
一共拼合O(n)次,这需要启发我们每次拼合都O(1)计算答案。
并且考虑T0一定长度大于S,所以我们可以O(n)预处理出来T0,考虑用字符串STR拼合T0,S在字符串STR上已经匹配了k位(k ∈ (1,|S|))的时候,在T0上接下来的贡献是多少。
然后考虑拼合,Ti = Txi + Tx2 ...... Txn,其中上面讲的就是,形如Txi + Tx2的这样的拼合一共最多1e6次,并且保证Tx2的前面一定是T0,而T0的信息我们已经预处理出来了。
问题就转化为了我们要O(1)处理X和Y拼合的问题,其中Y只会用到前|S|位,而前|S|位我们已经处理出来了在X中对于字符串S的kmp,已经匹配到了i,那么接下来在Y中会造成多少贡献。
我们只需要知道X中S能最长匹配到多少即可。
举个例子 X是ababc S是bcb,那么最长匹配长度就是2(bc),假设我们已经求出来了,就做完了。考虑如何求,我们就发现在拼合Ti的时候最后部分可以求,因为你Ti最后一部分一定是Txn + Di,而Txn的这一部分已经处理完了,只需要继续跑KMP,把Di这一段跑完即可,总复杂度是Di长度的和,所有Di的长度加起来是1e6,那就做完了。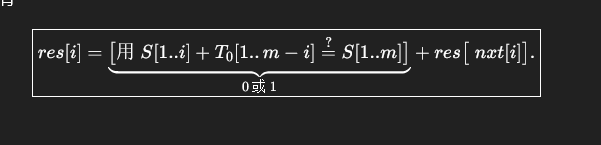
res求法就是,当前能否完成跨界匹配,再加上你跨界匹配成功后,要加上res[nxt[i]]表示额外能完成的其他跨界匹配。
code:
#include<bits/stdc++.h>
#define ull unsigned long long
using namespace std;
const int N=2e6+5;
string s,t,d;
int nw[N],res[N],to[N][2],nxt[N],n; // nw[i]:第i篇文章末尾匹配S的状态; res[i]:从状态i开始拼接T0能产生的匹配数; to[i][c]:KMP状态转移; nxt[i]:KMP失配函数
ull sum[N],pt[N],ps[N],pw[N]; // sum[i]:第i篇文章的匹配总数; pt[i]:T0前缀哈希; ps[i]:S前缀哈希; pw[i]:哈希底数的幂
int main(){
freopen("string.in","r",stdin);
freopen("string.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
cin>>s>>t;
int m=s.size(),k=t.size();
s=" "+s,t=" "+t;
// 计算T0的哈希值
for(int i=1;i<=k;i++){
if(t[i]=='0') pt[i]=pt[i-1]*13331+3;
else pt[i]=pt[i-1]*13331+7;
}
// 计算S的哈希值
for(int i=1;i<=m;i++){
if(s[i]=='0') ps[i]=ps[i-1]*13331+3;
else ps[i]=ps[i-1]*13331+7;
}
// 预计算哈希底数的幂
pw[0]=1;
for(int i=1;i<=max(m,k);i++)
pw[i]=pw[i-1]*13331;
// 构建KMP失配函数
for(int i=2;i<=m;i++){
int p=nxt[i-1];
while(p&&s[p+1]!=s[i]) p=nxt[p];
if(s[p+1]==s[i]) p++;
nxt[i]=p;
}
// 构建KMP状态转移表和预处理信息
for(int i=0;i<m;i++){
int v=s[i+1]-'0';
to[i][v]=i+1; // 匹配当前字符,状态+1
to[i][v^1]=to[nxt[i]][v^1]; // 不匹配,根据失配函数转移
// res[i]: 从匹配状态i开始,拼接T0能产生多少个完整匹配
if(i) res[i]=res[nxt[i]]+((ps[i]*pw[m-i]+pt[m-i])==ps[m]);
}
to[m][0]=to[nxt[m]][0],to[m][1]=to[nxt[m]][1]; // 完全匹配后的状态转移
res[m]=res[nxt[m]];
// 处理T0,计算S在T0中的出现次数和T0末尾的匹配状态
int p=0;
for(int i=1;i<=k;i++){
p=to[p][t[i]-'0'];
if(p==m) sum[0]++; // 完整匹配一次
}
nw[0]=p; // T0末尾的匹配状态
// 处理每个学生的文章
for(int i=1;i<=n;i++){
int k;
cin>>k;
int x;
// 拼接之前的文章
while(k--)
{
cin>>x;
sum[i]+=sum[x]; // 累加之前文章中的匹配数
if(k) sum[i]+=res[nw[x]]; // 如果不是最后一个拼接的文章,加上跨越拼接点的匹配数
}
// 处理当前文章末尾的匹配状态(来自最后拼接的文章)
int p=nw[x];
// 处理附加字符串Di
cin>>d;
for(int j=0;j<d.size();j++)
{
p=to[p][d[j]-'0'];
if(p==m) sum[i]++; // 在Di中找到完整匹配
}
nw[i]=p; // 记录当前文章末尾的匹配状态
cout<<sum[i]<<'\n';
}
return 0;
}







 浙公网安备 33010602011771号
浙公网安备 33010602011771号