20250725 DP优化

真的是太毒瘤了！

如果看到这里，请先看上一篇

蒙日矩阵

https://zhuanlan.zhihu.com/p/606424989

数据分块鸡

在鸡年来临之际，为了彻底打击程序猿及搬砖族的残余势力，计算鸡村的大数据计算中心需要应对大量的区间求和问题以进行合理规划。

区间求和是这么一个问题：给你长度为 ( n-1 ) 的数组，下标编号为 ([1, n])。有 ( q ) 个询问，其中第 ( j ) 个询问是要求下标区间在 ([l_j, r_j]) 内所有数的和。

数据分块鸡不会前缀和，它只知道分块大法好。它会将该数组切成若干小块，假设分界点为 ( a_0, a_1, a_2, \ldots, a_k )，其中 ( a_0 = 1, a_k = n )，那么第 ( i ) 块覆盖的下标区间即为 ([a_i, a_{i+1}])，并存储这个区域内所有元素的和。

每次查询 ([l_j, r_j]) 数据分块鸡总会尽可能利用整块存储的信息，并在边界处进行微调。会遇到如下几种情况：

1. 存在 ([a_i, a_{i+1})) 使得 ([l_j, r_j] = [a_i, a_{i+1}))：

   • 那么数据分块鸡将直接使用该块内存存储的元素总和，需要花费 1 的代价。

2. 如果不是上述情况，若存在 ([a_i, a_{i+1})) 使得 ([l_j, r_j] \subseteq [a_i, a_{i+1}))：

   • 那么数据分块鸡将会用该块内存存储的元素总和减去不在询问区间内的元素总和以求得答案，需要花费 ((l_j - a_i) + (a_{i+1} - r_j)) 的代价。

3. 如果不是上面任何一种情况，那么询问区间一定会跨越多个块。对于每一块：

   • 首先如果 ([a_i, a_{i+1}) \subseteq [l_j, r_j])：
     • 那么这一整块的元素总和将被加入答案，需要花费 1 的代价。
   • 除此之外，如果 ([a_i, a_{i+1})) 与 ([l_j, r_j]) 有交：
     • 那么 ([l_j, r_j]) 肯定是覆盖了该块的一个前缀或一个后缀。此时数据分块鸡会在如下两种计算方法里进行抉择，选取代价最小的计算方法：
       • 要么直接求和计算，花费的代价为两个区间交集的元素个数；
       • 要么拿块内元素总和减去不在询问区间内的元素总和，花费的代价为该块内包含的元素个数减去两个区间交集的元素个数。

最后总代价为每步的代价之和。

现在，给你 ( n ) 和这 ( q ) 个询问，请你帮数据分块鸡决定分块的分界点使得总代价最小吧！

---

输入格式

第一行两个正整数 ( n, q )。

接下来 ( q ) 行，每行三个整数 ( l_i, r_i )，表示询问区间 ([l_i, r_i])，保证 ( 1 \leq l_i < r_i \leq n )。

---

输出格式

输出共一行，一个整数表示最小代价。

---

样例一

输入

5 10
1 3
1 3
1 2
3 5
3 4
1 2
2 5
2 5
4 5

输出

13

---

一个简单的 DP 如下：记 fi 表示已经划分好 [1, i) 且最后分割点在 i 前的最小代价。记 w(l, r) 表示区间 [l, r) 的贡献，显然有 DPfi = minj<i
{fj + w(j, i)
为什么一开始想到的状态不是两位的？因为你发现第二维没啥用。

先考虑如何快速计算 w(l, r)，不难发现所有代价都可以转化为二维限制下的矩阵查，可以用主席树做到单次 O(log n)。w 看上去没有明显的性质，只能猜想 w 满足四边形不等式。大力讨论一下发现确实满足，于是可以直接套用二分法，时间复杂度 O(n log2 n

---

等等！ 什么是不难发现？ 明明很难发现。

我们对于w(l,r)，和mid = (l + r) >> 1；

我们把询问分成六类。

完全包含，完全被包含（或相等），左端点在l左且右端点在mid左/右，右端点在r右且左端点在mid右/左，不难发现这是一些二维偏序，可以用主席树做。

剩下的就是可以分治或者队列二分来做啦。

---

[PKUWC2018] Minimax

小 \(C\) 有一棵 \(n\) 个结点的有根树，根是 \(1\) 号结点，且每个结点最多有两个子结点。

定义结点 \(x\) 的权值为：

1.若 \(x\) 没有子结点，那么它的权值会在输入里给出，保证这类点中每个结点的权值互不相同。

2.若 \(x\) 有子结点，那么它的权值有 \(p_x\) 的概率是它的子结点的权值的最大值，有 \(1-p_x\) 的概率是它的子结点的权值的最小值。

现在小 \(C\) 想知道，假设 \(1\) 号结点的权值有 \(m\) 种可能性，权值第 \(i\) 小的可能性的权值是 \(V_i\)，它的概率为 \(D_i(D_i>0)\)，求：

\[\sum_{i=1}^{m}i\cdot V_i\cdot D_i^2 \]

你需要输出答案对 \(998244353\) 取模的值。

对于所有数据，满足 \(0 < p_i \cdot 10000 < 10000\)，所以易证明所有叶子的权值都有概率被根取到。

---

这个式子看似很可怕，实际上并不复杂。

就是左儿子出现j的概率加上右儿子出现j的概率。

其中又分为j是最大值的概率和j是最小值的概率。

这玩意可以用毒瘤的线段树合并来维护，你需要维护区间乘法标记和区间前缀和和后缀和。

---

int merge(int x, int y, int l, int r, int xmul, int ymul, int v) {
  if (!x && !y) return 0;
  if (!x) {
    pushmul(y, ymul);
    return y;
  }
  if (!y) {
    pushmul(x, xmul);
    return x;
  }
  pushd(x), pushd(y);
  int mid = l + r >> 1;
  int lsx = sum[ls[x]], lsy = sum[ls[y]], rsx = sum[rs[x]], rsy = sum[rs[y]];
  ls[x] = merge(ls[x], ls[y], l, mid, (xmul + 1ll * rsy % mod * (1 - v + mod)) % mod,
                (ymul + 1ll * rsx % mod * (1 - v + mod)) % mod, v);
  rs[x] = merge(rs[x], rs[y], mid + 1, r, (xmul + 1ll * lsy % mod * v) % mod,
                (ymul + 1ll * lsx % mod * v) % mod, v);
  pushup(x);
  return x;
}

这种单点独立修改的题有个套路，就是维护 fi 表示考虑前 i 题且不选 i 的最大收益，
gi 表示考虑后 n − i + 1 题且不选 i 的最大收益，和 hi 表示全局选 i 的最大收益，
然后 O(1) 回答询问

f的转移公式：

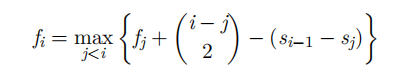
可以斜率优化，g同理。

H：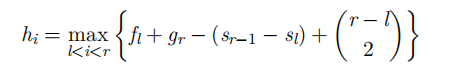

然后这个H非常难搞啊，hi​ 表示全局选择第 i 题时的最大收益。这意味着我们考虑所有包含 i 的连续子区间 [l,r]，

进行调整，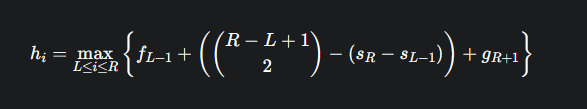

这个形式看起来复杂，因为它同时涉及到 L 和 R 两个变量，并且这两个变量之间还有约束 L≤i≤R。

这种同时优化两个变量的问题，一个经典的套路就是使用分治（CDQ 分治）。

这个就可以直接斜率优化了。

这个式子可以进一步变形为 YL​=KR​XL​+B 的形式。
令：

YL​=fL−1​+sL−1​+21​L(L−1)

XL​=L

KR​=R (斜率)

我们希望最大化 YL​−KR​XL​，这对应于最大化截距。
因此，我们需要维护一个上凸壳。

也就是说，在cdq的过程中，对于合并答案这一步，要维护两次，一次处理维护上凸包的斜率优化，一次是下凸包，这很复杂。

CDQ 分治中处理跨区贡献时的一个复杂点：通常需要进行两次斜率优化，一次对应 L 在左半边、R 在右半边，另一次对应 R 在右半边、L 在左半边（或者对称地看，是针对不同变量的斜率优化）。

为什么需要两次斜率优化？

我们把表达式展开并整理成 Y=kX+B 的形式。
为了方便处理，我们可以将与 L 相关的项组合成 A(L)，与 R 相关的项组合成 B(R)，以及一个 L⋅R 的交叉项。
比如，我们尝试把 hi​ 的更新拆分为两个独立的优化问题。

---