20250723 模拟赛 总结

不合法的情况只有起点练到了终点并且恰好无法全部染色为同种颜色。

考虑构造封死所有入口和放开所有出口，可以证明一定有解。

---

我计数很菜，所以我会写每一个部分分。

30分

从小到大加入数来 dp。暴力一点，既然要求连续三个的异或和不为
0，就记录序列的最后两个位置 𝑥, 𝑦 分别是什么，加入 𝑧 的时候要求
𝑥, 𝑦, 𝑧 异或和不为 0。
设f[i][x][y] <- f[i][y][z] && x xor y xor z != 0 && x < y < z
这是n^4;

40分

我们定义 dp[y][x] 表示以 x 为倒数第二个元素，y 为最后一个元素的“好”序列的数量

if ((i ^ j ^ k) != 0) dp[k][j] = (dp[k][j] + dp[j][i]) % mod;

注意到性质：如果连续三个位置 𝑎𝑖, 𝑎𝑖+1
, 𝑎𝑖+2 违反了题目的限制，那 (𝑎𝑖−1, 𝑎𝑖, 𝑎𝑖+1
) 就不可能违反限制了。设 𝑓(𝑛) 表示以𝑛 结尾有多少个合法的序列。使用容斥：𝑓(𝑛) = 1 +∑𝑖<𝑛𝑓(𝑖) − 𝐶，𝐶 是在 𝑛处第一次违反限制的序列数。𝐶 怎么算？如果一个序列 […, 𝑥, 𝑦, 𝑛] 在 (𝑥, 𝑦, 𝑛) 第一次违反限制，枚举 𝑦，如果𝑥 = (𝑦 ⊕ 𝑛) < 𝑦，𝐶就应该加上𝑓(𝑥)。时间复杂度 𝑂(𝑛^2)，期望得分 60

---

我们考虑类似KDT，进行分治，每次进行分割（规则和KDT一样）

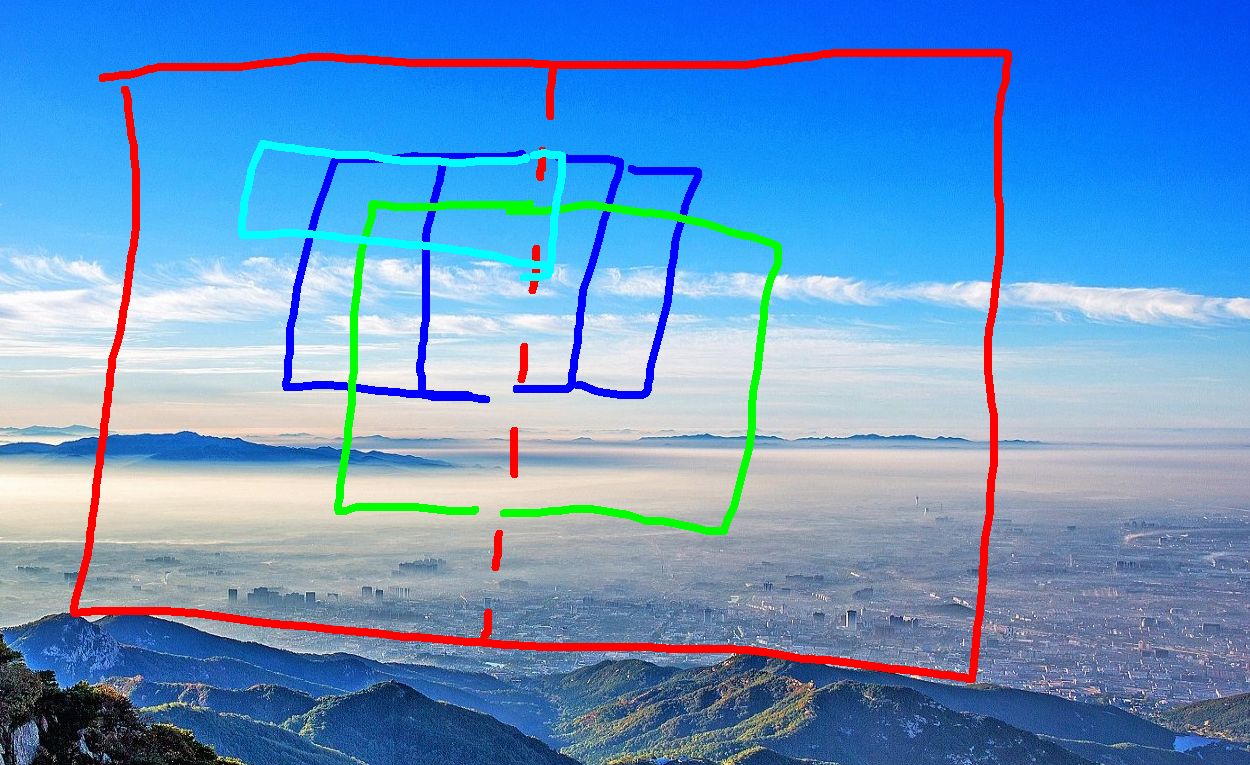
对于一次分割，我们如果能在O(nm)内求出来所有横跨分割线，并且在当前任务内的矩形数量就行了，那么对于一个上边界x和下边界y，答案就是所有(x,y)在左侧[的数量乘上右侧]的数量，例如图中深蓝色的答案就是2*2 = 4.

注，当前只考虑竖直分割，水平分割是同样的。

那么考虑如何计算，先计算Dxy表示xy这个点的颜色还能向下延申多少，这个可以Onm求出来，然后就可以求出来Ly表示对于当前这个分割线的y坐标为y的时候，能向左延申多少（这个由于分治的缘故可以暴力算）。那么一个半边的答案就是

因为递归有 log 𝑛𝑚 层，设短边长 𝑥 长边
长 𝑦，每层用 𝑥
2 + 𝑥𝑦 ≥ 2𝑥𝑦 也即 𝑂(𝑥𝑦)的时间处理了询问，加起来
每层是𝑂(𝑛𝑚)。可以通过本题得到 100 分

---

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

constexpr int MAXN = 2005;

char grid[MAXN][MAXN];
int cntl[MAXN][MAXN][2], cntr[MAXN][MAXN][2];
int to_left[MAXN][MAXN], to_right[MAXN][MAXN];
int len_l[MAXN], len_r[MAXN];
int to_left2[MAXN][MAXN];
int n, m;
ll ans = 0;

void solve(int xl, int xr, int yl, int yr) {
	if (xl >= xr || yl >= yr) return;
	
	if (xr - xl + 1 >= yr - yl + 1) {
		int mid = (xl + xr) >> 1;
		for (int i = yl; i <= yr; i++)
			for (int j = yl - 1; j <= yr + 1; j++)
				cntl[i][j][0] = cntl[i][j][1] = cntr[i][j][0] = cntr[i][j][1] = 0;
		
		for (int i = xl; i <= xr; i++) {
			for (int j = yl; j <= yr; j++) {
				if (j > yl && grid[i][j - 1] == grid[i][j])
					to_left[i][j] = to_left[i][j - 1];
				else
					to_left[i][j] = j;
			}
			for (int j = yr; j >= yl; j--) {
				if (j < yr && grid[i][j + 1] == grid[i][j])
					to_left2[i][j] = to_left2[i][j + 1];
				else
					to_left2[i][j] = j;
			}
		}
		
		for (int i = yl; i <= yr; i++) {
			len_l[i] = 0;
			for (int j = mid; j >= xl && grid[j][i] == grid[mid][i]; j--, len_l[i]++)
				cntl[i][to_left[j][i]][0]++, cntr[i][to_left2[j][i]][0]++;
					
					len_r[i] = 0;
					for (int j = mid + 1; j <= xr && grid[j][i] == grid[mid + 1][i]; j++, len_r[i]++)
						cntl[i][to_left[j][i]][1]++, cntr[i][to_left2[j][i]][1]++;
		}
		
		for (int i = yl; i <= yr; i++) {
			for (int j = yl; j <= yr; j++) {
				cntl[i][j][0] += cntl[i][j - 1][0];
				cntl[i][j][1] += cntl[i][j - 1][1];
			}
			for (int j = yr; j >= yl; j--) {
				cntr[i][j][0] += cntr[i][j + 1][0];
				cntr[i][j][1] += cntr[i][j + 1][1];
			}
		}
		
		for (int i = yl; i <= yr; i++) {
			for (int j = i + 1; j <= yr; j++) {
				if (grid[mid][i] != grid[mid][j]) continue;
				if (grid[mid][i] != grid[mid + 1][i]) continue;
				if (grid[mid][j] != grid[mid + 1][j]) continue;
				
				int res = (len_l[i] >= len_l[j]) ? cntl[j][i][0] : cntr[i][j][0];
				int res1 = (len_r[i] >= len_r[j]) ? cntl[j][i][1] : cntr[i][j][1];
				ans += 1LL * res * res1;
			}
		}
		solve(xl, mid, yl, yr);
		solve(mid + 1, xr, yl, yr);
	} else {
		int mid = (yl + yr) >> 1;
		for (int i = xl; i <= xr; i++)
			for (int j = xl - 1; j <= xr + 1; j++)
				cntl[i][j][0] = cntl[i][j][1] = cntr[i][j][0] = cntr[i][j][1] = 0;
		
		for (int i = yl; i <= yr; i++) {
			for (int j = xl; j <= xr; j++) {
				if (j > xl && grid[j - 1][i] == grid[j][i])
					to_left[j][i] = to_left[j - 1][i];
				else
					to_left[j][i] = j;
			}
			for (int j = xr; j >= xl; j--) {
				if (j < xr && grid[j + 1][i] == grid[j][i])
					to_left2[j][i] = to_left2[j + 1][i];
				else
					to_left2[j][i] = j;
			}
		}
		
		for (int i = xl; i <= xr; i++) {
			len_l[i] = 0;
			for (int j = mid; j >= yl && grid[i][j] == grid[i][mid]; j--)
				len_l[i]++, cntl[i][to_left[i][j]][0]++, cntr[i][to_left2[i][j]][0]++;
			
			len_r[i] = 0;
			for (int j = mid + 1; j <= yr && grid[i][j] == grid[i][mid + 1]; j++)
				len_r[i]++, cntl[i][to_left[i][j]][1]++, cntr[i][to_left2[i][j]][1]++;
		}
		
		for (int i = xl; i <= xr; i++) {
			for (int j = xl; j <= xr; j++) {
				cntl[i][j][0] += cntl[i][j - 1][0];
				cntl[i][j][1] += cntl[i][j - 1][1];
			}
			for (int j = xr; j >= xl; j--) {
				cntr[i][j][0] += cntr[i][j + 1][0];
				cntr[i][j][1] += cntr[i][j + 1][1];
			}
		}
		
		for (int i = xl; i <= xr; i++) {
			for (int j = i + 1; j <= xr; j++) {
				if (grid[i][mid] != grid[j][mid]) continue;
				if (grid[i][mid] != grid[i][mid + 1]) continue;
				if (grid[j][mid] != grid[j][mid + 1]) continue;
				
				int res = (len_l[i] >= len_l[j]) ? cntl[j][i][0] : cntr[i][j][0];
				int res1 = (len_r[i] >= len_r[j]) ? cntl[j][i][1] : cntr[i][j][1];
				ans += 1LL * res * res1;
			}
		}
		solve(xl, xr, yl, mid);
		solve(xl, xr, mid + 1, yr);
	}
}

int main() {
#ifndef OFLINE
	freopen("countcircle.in", "r", stdin);
	freopen("countcircle.out", "w", stdout);
#endif
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> (grid[i] + 1);
	solve(1, n, 1, m);
	cout << ans;
	return 0;
}