20250722 GF集训 数据结构
算术天才⑨与等差数列
cription
算术天才⑨非常喜欢和等差数列玩耍。
有一天,他给了你一个长度为 nn 的序列,其中第 ii 个数为 aiai。
他想考考你,每次他会给出询问 l,r,kl,r,k,问区间 [l,r][l,r] 内的数从小到大排序后能否形成公差为 kk 的等差数列。
当然,他还会不断修改其中的某一项。
为了不被他鄙视,你必须要快速并正确地回答完所有问题。
注意:只有一个数的数列也是等差数列。
考虑什么时候能组成等差数列。
首先max−min=(r−l)k
其次相邻两数差的绝对值的gcd是k
区间[l,r]内的数不重复
维护以下信息即可:
最大值,最小值,前驱的最大值,区间左端点数值,区间右端点数值,差的gcd
这里前驱指前面出现这个数的最后一个位置。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
constexpr int maxn = 1e6 + 10;
inline int gcd(int x, int y) {
return y == 0 ? x : gcd(y, x % y);
}
int n, m;
int a[maxn], prepos[maxn], nxtpos[maxn]; // prepos[i]: 上一个值相同的位置; nxtpos[i]: 下一个
map<int, int> mp_id; // 值 -> 组id
set<int> pos_set[maxn]; // 每个值组的所有位置(有序)
struct node {
int lval, rval;
int maxval, minval;
int preidx;
int gcdval;
};
inline int ls(int x) { return x << 1; }
inline int rs(int x) { return x << 1 | 1; }
node seg[maxn << 2];
inline node merge_node(const node &x, const node &y) {
node z;
z.lval = x.lval;
z.rval = y.rval;
z.maxval = max(x.maxval, y.maxval);
z.minval = min(x.minval, y.minval);
z.preidx = max(x.preidx, y.preidx);
z.gcdval = gcd(gcd(x.gcdval, y.gcdval), abs(x.rval - y.lval));
return z;
}
void build(int d, int l, int r) {
if (l == r) {
seg[d] = node{a[l], a[l], a[l], a[l], prepos[l], 0};
return;
}
int mid = (l + r) >> 1;
build(ls(d), l, mid);
build(rs(d), mid + 1, r);
seg[d] = merge_node(seg[ls(d)], seg[rs(d)]);
}
void update(int d, int l, int r, int p, const node &val) {
if (l > p || r < p) return;
if (l == r) {
seg[d] = val;
return;
}
int mid = (l + r) >> 1;
update(ls(d), l, mid, p, val);
update(rs(d), mid + 1, r, p, val);
seg[d] = merge_node(seg[ls(d)], seg[rs(d)]);
}
node query(int d, int l, int r, int L, int R) {
if (L <= l && r <= R) return seg[d];
int mid = (l + r) >> 1;
if (R <= mid) return query(ls(d), l, mid, L, R);
if (L > mid) return query(rs(d), mid + 1, r, L, R);
node x = query(ls(d), l, mid, L, R);
node y = query(rs(d), mid + 1, r, L, R);
return merge_node(x, y);
}
inline node make_leaf(int idx) {
return node{a[idx], a[idx], a[idx], a[idx], prepos[idx], 0};
}
int main() {
#ifdef OFLINE
freopen("in.in", "r", stdin);
freopen("out.ouw", "w", stdout);
#endif
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m;
int grp_cnt = 0;
for (int i = 1; i <= n; ++i) {
cin>>a[i];
auto it = mp_id.find(a[i]);
if (it == mp_id.end()) {
mp_id[a[i]] = ++grp_cnt;
pos_set[grp_cnt].insert(i);
prepos[i] = 0;
nxtpos[i] = 0;
} else {
int gid = it->second;
int prv = *--pos_set[gid].end();
prepos[i] = prv;
nxtpos[prv] = i;
nxtpos[i] = 0;
pos_set[gid].insert(i);
}
}
build(1, 1, n);
int last_ans = 0;
for (int qi = 1; qi <= m; ++qi) {
int opt;
cin>>opt;
if (opt == 1) {
int x, y;
cin>>x>>y;
x ^= last_ans;
y ^= last_ans;
int oldv = a[x];
int old_gid = mp_id[oldv];
pos_set[old_gid].erase(x);
int p = prepos[x];
int q = nxtpos[x];
if (p) nxtpos[p] = q;
if (q) {
prepos[q] = p;
update(1, 1, n, q, make_leaf(q));
}
int new_gid;
auto it = mp_id.find(y);
if (it == mp_id.end()) {
mp_id[y] = ++grp_cnt;
new_gid = grp_cnt;
pos_set[new_gid].insert(x);
prepos[x] = 0;
nxtpos[x] = 0;
} else {
new_gid = it->second;
auto &S = pos_set[new_gid];
auto lb = S.lower_bound(x);
if (lb == S.begin()) {
prepos[x] = 0;
nxtpos[x] = *lb;
prepos[*lb] = x;
update(1, 1, n, *lb, make_leaf(*lb));
} else if (lb == S.end()) {
auto itp = lb; --itp;
prepos[x] = *itp;
nxtpos[x] = 0;
nxtpos[*itp] = x;
} else {
auto itp = lb; --itp;
int pv = *itp;
int nx = *lb;
prepos[x] = pv;
nxtpos[x] = nx;
nxtpos[pv] = x;
prepos[nx] = x;
update(1, 1, n, nx, make_leaf(nx));
}
S.insert(x);
}
a[x] = y;
update(1, 1, n, x, make_leaf(x));
} else {
int L, R, z;
cin>>L>>R>>z;
L ^= last_ans;
R ^= last_ans;
z ^= last_ans;
if (L > R) swap(L, R);
if (L < 1) L = 1;
if (R > n) R = n;
node res = query(1, 1, n, L, R);
bool ok = true;
ok &= (res.maxval - res.minval == z * (R - L));
ok &= (res.gcdval == z || res.gcdval == 0);
ok &= (res.preidx < L || z == 0);
if (ok) {
++last_ans;
puts("Yes");
} else {
puts("No");
}
}
}
return 0;
}
Tree Generator™ *

Owl 写下了一棵 n 个结点的有根树的描述。之后,他又写了 q 次新的描述。每次写新描述时,他会从上一次写下的描述中选出两个不同的位置,交换这两个括号,并将结果写下来。他始终确保每次写下的字符串都能描述一棵有根树。
若从序列中任取一段连续子序列,从中去掉所有匹配括号后,剩下的括号组成的路径一定为一条链,链长为剩下的子序列长。
树上直径长度即为任意区间去掉匹配括号后的长度的最大值。
所以 最长去匹配区间 = 最大的(将区间分成两段)后面的权值和 - 前面的权值和
在线段树维护这些信息:
sum 表示 sum(l,r)
lmx 表示 maxsum(l,k)
rmx 表示 maxsum(k,r)
lmn 表示 minsum(l,k)
rmn 表示 minsum(k,r)
mx1 表示 maxsum(x,y)−sum(l,x),l≤x≤y≤r
mx2 表示 maxsum(y,x)−sum(x,y),l≤x≤y≤r
mx 表示 maxsum(y,z)−sum(x,y),l≤x≤y≤z≤r
void pushup(int k){
s[k].sum=s[k<<1].sum+s[k<<1|1].sum;
s[k].lmx=max(s[k<<1].lmx,s[k<<1].sum+s[k<<1|1].lmx);
s[k].lmn=min(s[k<<1].lmn,s[k<<1].sum+s[k<<1|1].lmn);
s[k].rmx=max(s[k<<1|1].rmx,s[k<<1|1].sum+s[k<<1].rmx);
s[k].rmn=min(s[k<<1|1].rmn,s[k<<1|1].sum+s[k<<1].rmn);
s[k].mx1=max(s[k<<1].mx1,max(-s[k<<1].sum+s[k<<1|1].mx1,s[k<<1|1].lmx+s[k<<1].rmx*2-s[k<<1].sum));
s[k].mx2=max(s[k<<1|1].mx2,max(s[k<<1|1].sum+s[k<<1].mx2,-s[k<<1].rmn+s[k<<1|1].sum-2*s[k<<1|1].lmn));
s[k].mx=max(max(s[k<<1].mx,s[k<<1|1].mx),max(s[k<<1].mx2+s[k<<1|1].lmx,-s[k<<1].rmn+s[k<<1|1].mx1));
}
AT_arc069_d [ARC069F] Flags
考虑2-SAT,但是建图是n^2的,用线段树优化即可,可以写的非常暴力,但是显然不好。
用第一篇题解的做法。
PERIODNI
运输规划
有 n 个城市,对于任意 1<i≤n 满足第 i 个城市与第 i−1 个城市间有一条双向的道路,每个城市有一个对卡车高度的限制 hi,代表只有高度小于等于 hi 的卡车可以从这个城市经过,现在有 m 个城市 S1,S2,...,Sm 各有恰好一个运输任务,任务要求编号为 i 且高度为 hSi 的卡车从城市 Si 出发到达任意一个有机场的城市,而有 m 个城市有机场,分别为 T1,T2,...,Tm,对于一个合法的运输方案而言,需要保证每个卡车都到达一个机场且每个机场恰好有一辆卡车抵达。一个机场可以同时被多辆卡车经过。请注意,如果你无法经过某个城市,那么你也无法抵达这个城市。
记 ci 表示抵达位于城市 Ti 的机场的的卡车编号,令数组 F={c1,c2,...,cm},请你最小化 F 的字典序并输出 F。
我们定义两个长度为 len 的数组 A,B 满足 A 的字典序小于 B 当且仅当存在 0≤i<len 满足对于任意 1≤j≤i 满足 Aj=Bj 且 Ai+1<Bi+1。
数据保证有解,保证所有 hi 互不相同,所有 Ti 互不相同,所有 Si 互不相同。但是可能会存在 i,j 满足 Si=Tj
问题转化与笛卡尔树
卡车可达性: 题目中城市 i 到 i−1 有双向道路,且每个城市有高度限制 hi。这意味着卡车只能通过高度不大于其自身高度的城市。所有 hi 互不相同,这引出了一个关键性质:对于任意一个城市 u,能够通过 u 的卡车,可以通过 u 左右两侧延伸出去,直到遇到比 hu 小的城市。这个结构与笛卡尔树的性质非常吻合。
笛卡尔树构建: 我们可以将城市看作节点,以城市编号为横坐标,城市高度 hi 为权值,构建一棵笛卡尔树。具体来说,对于城市 i,它将是其左侧第一个高度大于 hi 的城市和右侧第一个高度大于 hi 的城市之间的高度最大的城市。这样,任意一个城市 u 及其子树中的所有城市,都是可以通过 u 的卡车可达的。
实现细节: 使用单调栈构建笛卡尔树。遍历城市 i 从 1 到 n。维护一个单调递减的栈(按高度)。当遇到一个城市 i,如果栈顶城市的高度大于 hi,则将栈顶城市出栈,并将其作为当前城市 i 的左孩子。重复此过程直到栈为空或栈顶城市高度小于 hi。然后将当前城市 i 压入栈。如果栈不为空,则栈顶城市是 i 的父节点。
笛卡尔树的含义: 在构建出的笛卡尔树中,如果城市 A 是城市 B 的祖先,那么从城市 B 出发的卡车可以通过城市 A。也就是说,一辆卡车能通过的所有城市构成了笛卡尔树上从其出发城市到根节点的路径。
-
贪心策略与霍尔定理
最小化字典序: 题目要求最小化输出数组 F 的字典序。这意味着我们应该优先为编号小的机场分配尽可能小的卡车编号。因此,我们将机场 Ti 按照其编号 i 排序,然后依次为每个机场分配卡车。
合法分配的条件(霍尔定理): 为了保证每个机场都能被分配到一辆卡车,并且每个卡车都抵达一个机场,我们可以联想到二分图完美匹配问题。在这里,左部点是卡车(以其编号表示),右部点是机场。一条边 (Si,Tj) 存在当且仅当编号为 i 且高度为 hSi 的卡车可以到达城市 Tj。
霍尔定理告诉我们,一个二分图存在完美匹配当且仅当对于左部点任意子集 X,其邻域 N(X) 的大小 ∣N(X)∣≥∣X∣。在本题中,我们关心的是子树内的“机场数 - 卡车数”的差值。如果某个子树的这个差值小于 0,说明这个子树内的卡车数量多于机场数量,必然无法全部匹配,导致无解。因此,我们需要保证在任何时候,对于笛卡尔树中的任意一个节点 u,其子树中包含的机场数量 ≥ 子树中包含的卡车数量。
为了动态维护“机场数 - 卡车数”的差值以及查询路径上的最小卡车编号,我们使用树链剖分和两棵线段树。
线段树 1 (Seg1):维护 min(cnt_air[u] - cnt_truck[u])
线段树 2 (Seg2):维护路径上的最小卡车编号
贪心匹配: 遍历机场编号 i 从 1 到 m。对于当前机场 Ti:
find_lim(t): 向上找到一个限制点 v。这个点 v 是 Ti 到根路径上,满足 s1_min(1, 1, n, dfn[top_[u]], dfn[u]) <= 0 的最深节点。这意味着从 v 子树(包含 Ti)开始向上,所有祖先节点子树的“机场数 - 卡车数”差值都 ≥0。我们需要在这个 v 的子树内,或者更准确地说,在 Ti 到 v 的路径上(在笛卡尔树上),寻找匹配的卡车。
find_lim 函数通过树链剖分,不断向上查询路径上的 s1_min 值。如果当前重链上的最小值大于 0,则继续跳到重链顶部的父节点。否则,就在当前重链上二分查找第一个小于等于 0 的点。
path_min(t, v): 在 Ti 到 v 的路径上查询可用的、编号最小的卡车。
记录结果并更新:
将找到的卡车编号存入 ans[i]。
更新 Seg1:因为 Ti 机场被匹配,以及 pick.id 卡车被匹配,这会改变它们所在子树的“机场数 - 卡车数”差值。具体是,从 pick.id 到根节点路径上的所有节点的 cnt_truck 减少 1 (在差值上体现为 +1),从 T_i 到根节点路径上的所有节点的 cnt_air 减少 1 (在差值上体现为 -1)。使用 path_add 函数在 Seg1 上进行更新。
更新 Seg2:将 pick.id 对应的线段树位置设为 INFV,表示该卡车已被使用。
[CERC2013] Escape
这个地牢是由 n 个房间和 n−1 条走廊连接组成的树状结构,英雄一开始在 1 号房间,而且他只有抵达 t 号房间才能逃离这个地牢。从 1 号房间出发可以抵达任何一个其它的房间,可惜的是,在经历激烈的战斗后,英雄的精力使用完了,所以一开始该英雄的精力为 0,并且一旦英雄的精力低于 0,那么英雄就会当场逝世,以悲剧结束。在这些房间中,里面暗藏玄机,里面可能有怪兽,也有可能是可以补充精力的魔泉,当然也可能什么也没有,如果是怪兽,那么英雄就必须与它战斗从而消耗一些精力,如果是魔泉,那么英雄可以补充自己的精力。所有的怪兽只会战斗一次,所有的魔泉只能使用一次。(换句话说就是所有的精力的上升或者下降只会发生在第一次访问这个房间的时候)
英雄的精力没有上限,每一个房间都可以反复走多次。
设 fu,i 表示以 i 的血量进入子树 u 中最多可以获得 fu,i 的血量。
假如当前有若干个最简二元组(x,y)表示表示如果当前血量 ≥x ,则可以再额外加上 y
那么通过以下流程可以弄出来f
初始令 HP=i
取出当前 gu 中 x 最小的那个二元组 (x,y) ,如果 **HP<x**(这里题解笔误了我想了半天) 就结束,否则让 HP←HP+y ,并删掉二元组 (x,y)
重复上述步骤
最后得到的 HP 就是 fu,i+i 。
考虑如何合并出来这些二元组,考虑从树上从下往上合并
au>0
直接往当前集合中丢入一个 (0,au)
au<0
我们令 cur 表示以当前 HP 状态下能额外提供的血量为 cur ,L 表示如果要进入子树 u ,初始的 HP 至少应该为多少。
初始令 cur=au,L=−au,表示初始至少有 −au 的血才能进入,能够额外得到 au 的血量。
取出最小的二元组 (x,y)
如果 x≤L\orcur<0 ,就令 L←max(L,x−cur),cur←cur+y
重复上述操作直到集合为空或者不满足条件
如果最后 cur>0 ,就往集合中加入二元组 (L,cur)
显然这是对的。
用DSU+堆两个log,用可并的一个log但是懒得写了。
教训: 记得删cerr,否则你会像我一样卡常熟卡半天
注意,关于判断合法,直接从T连一个n+1,然后n+1回复特别大,最后在根判断大不大即可。
#include<bits/stdc++.h>
using namespace std;
constexpr int maxn = 2e5+10;
#define int long long
struct edge{
int to,next;
}e[maxn * 2];
int head[maxn], cnt;
int w[maxn];
void addedge(int u,int v){
e[++cnt].to = v;
e[cnt].next = head[u];
head[u] = cnt;
}
#define Pair My_Pair
struct Pair{
int x,y;
bool operator<(const Pair& other) const {
if (x != other.x)
return x > other.x;
return y > other.y;
}
};
priority_queue<Pair> q[maxn];
using hep = priority_queue<Pair>;
void merge(hep &x, hep &y) {
if (&x == &y) return;
if (x.size() < y.size()) swap(x, y);
while (!y.empty()) {
x.push(y.top());
y.pop();
}
}
void dfs(int x,int f){
for(int i = head[x];i;i = e[i].next){
int y = e[i].to;
if(y == f) continue;
dfs(y,x);
merge(q[x],q[y]);
}
if(w[x] > 0){
q[x].push((Pair){0,w[x]});
}
else{
int cur = w[x],L = 0 - w[x];
while(!q[x].empty()){
//cerr<<1<<endl;
int X = q[x].top().x,y = q[x].top().y;
if(X <= L || cur < 0){
L = max(L,X - cur);
cur += y;
}
else{
break;
}
q[x].pop();
}
if(cur > 0){
q[x].push((Pair){L,cur});
}
}
}
void init(){
cnt = 0;
memset(head, 0, sizeof(head));
for(int i = 1; i < maxn; ++i){
while(!q[i].empty()) q[i].pop();
}
}
int n, t;
constexpr int INF = 1e18;
signed main(){
#ifdef OFLINE
freopen("in.in","r",stdin);
freopen("out.ouw","w",stdout);
#endif
int T;
cin>>T;
while(T --> 0){
init();
cin>>n>>t;
for(int i = 1;i <= n;i++){
cin>>w[i];
}
for(int i = 1;i < n;i++){
int x,y;
cin>>x>>y;
addedge(x,y);
addedge(y,x);
}
addedge(n+1, t);
addedge(t, n+1);
w[n+1] = INF;
dfs(1,0);
int hp = 0;
while(!q[1].empty() && hp >= q[1].top().x){
hp += q[1].top().y;
q[1].pop();
}
if(hp * 2 >= INF) cout<<"escaped"<<endl;
else cout<<"trapped"<<endl;
}
return 0;
}
归约 / CNF-SAT

考虑DP[i][j]表示当前已经确定了前i个,没有处理完的限制(即限制匹配到当前i仍然都匹配)的最左边的l的位置是j。
瓶颈在于求出j,暴力是n^3,如何优化?
考虑对所有限制在当前没有i以前被截断的部分倒置建立字典树。
每次就只需要查询一个点i如果下一个是0/1没有匹配/匹配,会转移到哪个点(fa[i])。
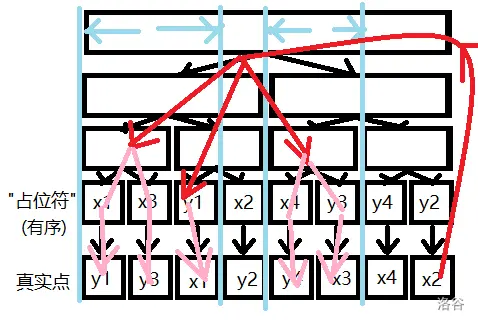
考虑用虚的树,不是虚树维护:
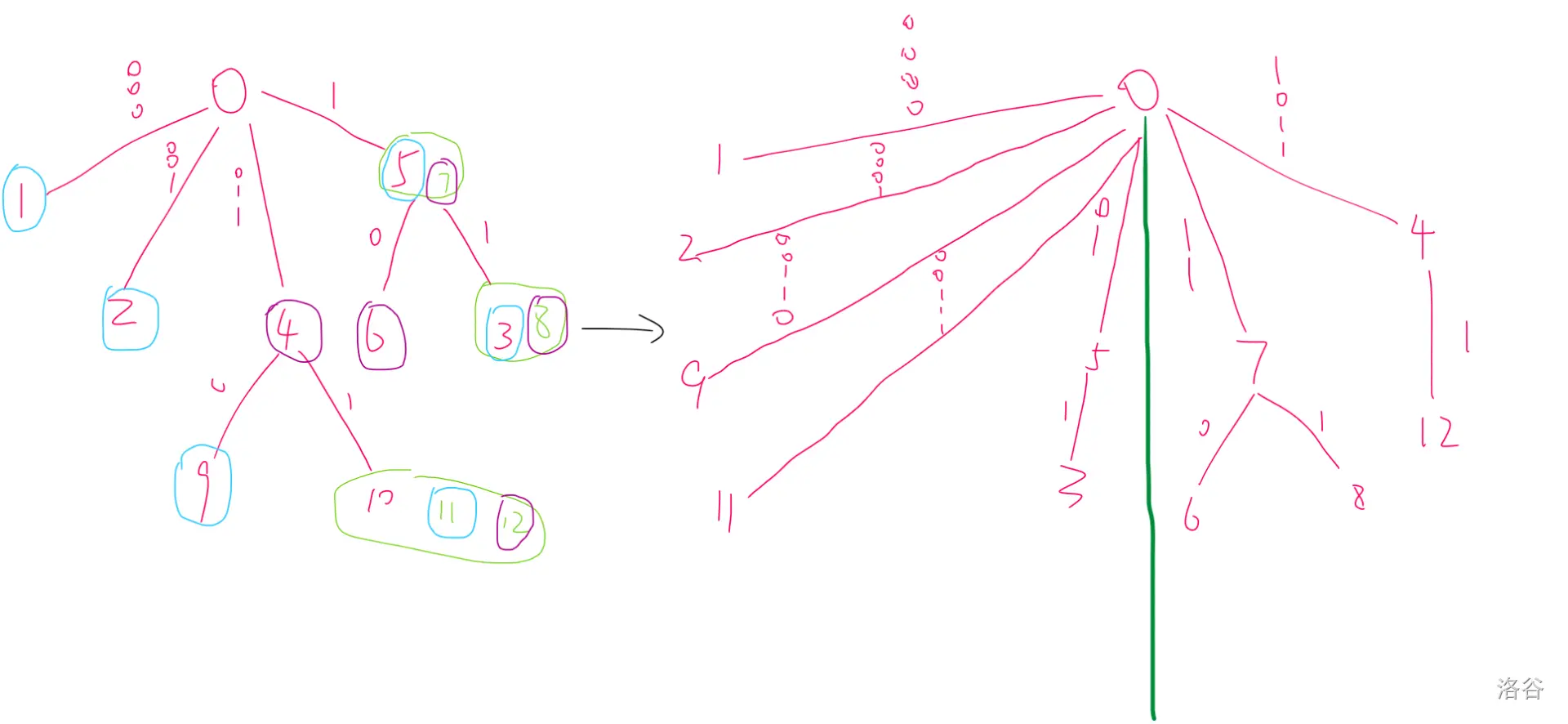
那么每个可能的状态一定是字典树上的一条链(因为已经匹配的后缀都相匹配)。
那么每次更新fa相当于对于当前这个状态找出处理完后下一个j(没有处理完的限制(即限制匹配到当前i仍然都匹配)的最左边的l的位置是j。)的位置,这个可以直接求。
然后考虑如何维护字典树在根加入一个字符,这个看图即可,蓝色的是分界线。
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pli = pair<ll, int>;
using pi = pair<int, int>;
template<typename A>
using vc = vector<A>;
template<typename A, const int N>
using aya = array<A, N>;
inline int read() {
int s = 0, w = 1;
char ch;
while ((ch = getchar()) > '9' || ch < '0') if (ch == '-') w = -1;
while (ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
return s * w;
}
inline int read(char &ch) {
int s = 0, w = 1;
while ((ch = getchar()) > '9' || ch < '0') if (ch == '-') w = -1;
while (ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
return s * w;
}
const int mod = 1000000007;
// fa[p] 表示当 x_i 取一个值时,子句 p 在虚树上的新父节点(即新的最左未满足子句)
// fap[p] 表示当 x_i 取另一个值时,子句 p 在虚树上的新父节点
// 这里的 fa 和 fap 存储的是子句的编号
int fa[1000005], fap[1000005];
//虚树节点 num 的子节点
vc<int> son[1000005];
//虚树节点 num 的所有子句的编号
vc<int> bel[1000005];
// dp[i][j] 表示当前确定了前 i 个变量,且最左未满足子句为 j 时的方案数
map<int, ll> dp[1000005];
// 所有以 x_i 为最左变量的子句的编号
vc<int> l[1000005];
// 第 m 个子句的所有文字(正数表示 x_k,负数表示 ~x_k)
// a[m][0] 存储的是该子句的第一个文字的绝对值,即其左端点 l_m
vc<int> a[1000005];
// node 存储当前迭代中,所有在 dp[i-1] 中有值的 'j' 状态,以及新加入的节点
vc<int> node;
int n;
inline int get(int x, int y) {
// 这里的下标计算有点特殊,因为a[x]的元素是按变量绝对值排好序的
// abs(a[x][0]) 是子句x的最小变量下标,y 是当前处理的变量下标
// a[x][y - abs(a[x][0])] 应该是指在子句x的内部表示中,x_y 对应的文字
// 保证了子句中的变量是连续区间的性质。
// 比如如果子句是 (x2 v ~x3 v x4), 那么a[m]中可能存 {2, -3, 4} (经过排序)
// abs(a[m][0])就是2
// 当 y=2时, y-abs(a[m][0]) = 0, 取a[m][0]
// 当 y=3时, y-abs(a[m][0]) = 1, 取a[m][1]
// 当 y=4时, y-abs(a[m][0]) = 2, 取a[m][2]
return a[x][y - abs(a[x][0])];
}
// num: 当前在虚树中处理的节点(代表一个子句编号),0 表示虚树的根
// f0: 当 x_i 取 False 时,当前 num 节点应连接到的新父节点(新的最左未满足子句)
// f1: 当 x_i 取 True 时,当前 num 节点应连接到的新父节点
// i: 当前处理的变量下标 (x_i)
// f: 一个标记,表示当前路径上是否已经有子句成立。如果为 true,表示当前状态已经无效,不应该转移。
void dfs(int num, int f0, int f1, int i, bool f) {
vc<int> nod0, nod1; // nod0 存储 x_i 取 False 时满足的子句,nod1 存储 x_i 取 True 时满足的子句
int rt0 = 0, rt1 = 0; // rt0, rt1 分别是 nod0 和 nod1 中左端点最小的子句编号
// 这里的 bel[num] 存储的是在 i-1 状态下,以 num 为最左未满足子句的集合
for (int p : bel[num]) {
// 如果子句 p 的右端点 abs(a[p].back()) 小于 i,
// 说明该子句的范围在 i 之前就已经完全确定,并且它在 i-1 时仍然是未成立的(因为被包含在 bel[num] 中)
// 那么在处理到 i 时,它肯定不成立,此路径无效。
if (abs(a[p].back()) < i) {
f = true; // 标记当前路径无效
} else { // 如果子句 p 穿过或开始于 i
if (get(p, i) > 0) { // 如果子句 p 中 x_i 是正文字 (x_i)
nod1.push_back(p); // 放入 nod1 (x_i 取 True 时满足)
} else { // 如果子句 p 中 x_i 是负文字 (~x_i)
nod0.push_back(p); // 放入 nod0 (x_i 取 False 时满足)
}
}
}
// 清空当前 num 节点的 bel 和 son,因为它们将在下一层重新构建
vc<int> mem = son[num]; // 备份子节点,用于递归
bel[num].clear();
son[num].clear();
// 处理 nod0 集合:当 x_i 取 False 时满足的子句
if (nod0.size()) {
rt0 = nod0[0]; // nod0[0] 是其子句中最靠左的(因为是排好序的)
bel[rt0] = nod0; // 将 nod0 中的子句归属到 rt0 节点
son[f0].push_back(rt0); // 将 rt0 作为 f0 的子节点(在虚树中)
f0 = rt0; // 更新 f0 为 rt0,向下递归时作为新的父节点
}
// 处理 nod1 集合:当 x_i 取 True 时满足的子句
if (nod1.size()) {
rt1 = nod1[0]; // nod1[0] 是其子句中最靠左的
bel[rt1] = nod1; // 将 nod1 中的子句归属到 rt1 节点
son[f1].push_back(rt1); // 将 rt1 作为 f1 的子节点
f1 = rt1; // 更新 f1 为 rt1
}
// 如果当前路径有效 (f 为 false,即没有子句在 rk < i 的情况下仍未满足)
if (!f) {
// 构建当前节点 num 在 x_i 两种取值下的新父节点
if (rt0) { // 如果 x_i 取 False 时有满足的子句 (rt0 存在)
fa[rt0] = f1; // 当 x_i 取 False 时,rt0 成立,其贡献会传递给 dp[i][f1] (即当 x_i 取 True 时的新状态)
// 实际上 rt0 应该指向0,因为其本身成立了。这里fa[rt0]=f1 是指 rt0 的“另一条路径”(取True)的父节点。
// 这是一个巧妙的编码方式,fa[rt0]表示当x_i取False时,rt0成立了,此时这条dp路径就该转移到f1表示的状态
// 但如果rt0不成立,而是它本身就代表了当前最左未满足的子句,那么它会保留在虚树中。
node.push_back(rt0); // 将 rt0 加入 node 列表,以便后续 dp 转移时遍历
fap[rt0] = rt0; // 当 x_i 取 True 时,rt0 不成立,它的新父节点就是它自己(因为它本身就是最左的)
// 这是一个交叉的赋值,fa[rt0] 对应 x_i取False,fap[rt0] 对应 x_i取True
// 实际含义是,如果某个子句 (比如rt0) 在x_i取False时成立,那么它原本的方案数会贡献到当x_i取True时对应的状态f1
// 如果rt0在x_i取True时不成立,那么它自身就是新的最左未满足子句,所以fap[rt0]=rt0
}
if (rt1) { // 如果 x_i 取 True 时有满足的子句 (rt1 存在)
fa[rt1] = f0; // 当 x_i 取 True 时,rt1 成立,其贡献会传递给 dp[i][f0] (即当 x_i 取 False 时的新状态)
node.push_back(rt1); // 将 rt1 加入 node 列表
fap[rt1] = rt1; // 当 x_i 取 False 时,rt1 不成立,它的新父节点就是它自己
}
}
// 如果是虚树的根节点(num=0)
if (!num) {
fa[0] = f0; // 根节点0的 fa (x_i 取 False 时的状态) 为 f0 (最左未满足子句)
fap[0] = f1; // 根节点0的 fap (x_i 取 True 时的状态) 为 f1 (最左未满足子句)
}
for (int p : mem) dfs(p, f0, f1, i, f);
}
int main() {
#ifdef OFLINE
freopen("in.in","r",stdin);
freopen("out.ouw","w",stdout);
#endif
n = read();
a[0].push_back(0);
int m = 0; // 子句计数器
while (1) {
char ch;
while (((ch = getchar()) != '(') && (ch != EOF));
if (ch != '(') break;
m++;
while (true) {
ch = getchar();
bool f = false;
if (ch == '~') {
f = true;
ch = getchar();
}
int v = read(ch);
if (f) v = -v;
a[m].push_back(v);
if (ch == ')') break;
getchar(); // 跳过 ' '
getchar(); // 跳过 'v'
}
sort(a[m].begin(), a[m].end(), [](int x, int y) { return abs(x) < abs(y); });
l[abs(a[m][0])].push_back(m);
}
//确定 0 个变量时,没有未满足的子句,有 1 种方案
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
// bel[0] 包含了所有以 x_i 为最左变量的子句 (l_k = i)
bel[0] = l[i];
sort(bel[0].begin(), bel[0].end()); //保证 rt0/rt1 正确
node.clear();
// dfs(0, 0, 0, i, false) 表示从虚树的根节点开始,初始 f0, f1 都是 0,当前变量是 i,初始没有无效路径
dfs(0, 0, 0, i, false);
node.push_back(0);
for (int p : node) {
if (dp[i - 1].count(p)) { // 如果 dp[i-1][p] 存在方案数
// 将 dp[i-1][p] 的方案数转移到 dp[i]
// fa[p] 对应 x_i 的某种取值(例如False)后,p 状态转移到的新状态 j'
// fap[p] 对应 x_i 的另一种取值(例如True)后,p 状态转移到的新状态 j''
// 这两个值在 dfs 中被计算并存储
(dp[i][fa[p]] += dp[i - 1][p]) %= mod;
(dp[i][fap[p]] += dp[i - 1][p]) %= mod;
}
}
}
printf("%lld\n", dp[n][0]);
return 0;
}

你可能无法相信,但是标签只有树状数组

然后证明略



这是一个李超树合并,可以用DSU做,但是李超线段树是可以合并的。
我们回顾以下李超树。
其实就是线段树,只不过每个节点维护的值是线段。
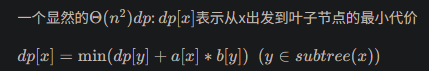
考虑对于点a[x],如果b[x]是斜率,dp是截距,就是一个线段,每次查询最小值即可。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
// CF932F - Escape Through Leaf
// 李超线段树合并实现(带详细注释)
// 修正版:修复了在将 nodePool 条目接到空子树时未清空其子指针导致的结构重复/错误问题。
static const int MAXN = 100000 + 5;
static const int BASE = 100000; // 坐标偏移:把 x −1e5..1e5 映到 0..2e5
static const int MAXW = 200000; // 映射后 x 的取值范围 [0, MAXW]
static const ll INF = (ll)4e18; // 足够大的正无穷(避免溢出)
int n;
int a[MAXN], bval[MAXN]; // 题中 b_i 与下面 rec 的 c 字段命名会有冲突,这里叫 bval
ll dp[MAXN];
// rec[i] 表示编号为 i 的 "线": y = m * x + c
struct Line {
ll m; // 斜率(对应题中 b_v)
ll c; // 截距(对应 dp[v])
} rec[MAXN];
// 计算线 id 在 x=pos 时的值。这里 pos 为映射后的值(已加 BASE)
inline ll eval(int id, int pos) {
ll x = (ll)pos - BASE; // 恢复原始 x
return rec[id].m * x + rec[id].c;
}
// 树的邻接表
vector<int> g[MAXN];
// 李超线段树的节点结构 —— 注意:每条线分配一个 nodePool 条目作为其容器
struct Node {
int lson, rson; // 子节点索引(在 nodePool 中)
int line_id; // 指向 rec 中哪条线在该树结点上驻留
} nodePool[MAXN]; // 分配 n 个条目:每个原始树结点分配一个 nodePool 条目
int idtot = 0; // nodePool 的已用计数(也用作分配代表某条线的树结点)
int root[MAXN]; // root[u] 保存子树 u 的李超线段树根(nodePool 的下标),为空为 0
// update:把 nodePool 条目 y(携带一条线 line_id,且可能已有子指针)插入到
// 以 cur 为根、区间 [l,r] 的李超线段树中。
// 设计要点:当 cur==0(空位)时我们只把 y 的 "线信息" 接上(清空其子指针)——
// 避免把还未合并的子结构重复挂上。
void update(int &cur, int l, int r, int y) {
if (!cur) {
// 当前子树为空:我们把 y 挂上,但为了避免重复移动未合并的子树,
// 只接入 y 的线信息并清空子指针(与经典实现保持一致)。
cur = y;
nodePool[cur].lson = nodePool[cur].rson = 0;
return;
}
// 当前结点已有一条线(idA),新插入线为 idB(存在于 nodePool[y].line_id 中)
int idA = nodePool[cur].line_id;
int idB = nodePool[y].line_id;
// 端点剪枝:若 idA 在端点都 <= idB,则 idA 在整段都不比 idB 差,直接返回
if (eval(idA, l) <= eval(idB, l) && eval(idA, r) <= eval(idB, r)) {
return;
}
// 若 idB 在端点都 <= idA,则 idB 在整段更好,直接把当前结点的线替换为 idB
if (eval(idB, l) <= eval(idA, l) && eval(idB, r) <= eval(idA, r)) {
nodePool[cur].line_id = idB;
return;
}
int m = (l + r) >> 1;
// 中点比较:决定谁在中点更优,把那条放到当前结点,输掉的下放
if (eval(idB, m) < eval(idA, m)) {
swap(nodePool[cur].line_id, nodePool[y].line_id);
}
// 重新读取(现在 nodePool[y] 为要下放的线)
idA = nodePool[cur].line_id;
idB = nodePool[y].line_id;
// 根据端点比较决定下放到左子区间或右子区间
if (eval(idB, l) < eval(idA, l)) {
update(nodePool[cur].lson, l, m, y);
} else if (eval(idB, r) < eval(idA, r)) {
update(nodePool[cur].rson, m + 1, r, y);
}
}
// mergeTrees:合并两棵李超线段树 x 和 y(对应相同区间 [l,r]),返回合并后的根
// 思路:先递归合并左右子树(把 y 的子树合并到 x 的对应子树),最后把 y 当前结点的线插入 x
int mergeTrees(int x, int y, int l, int r) {
if (!x) return y;
if (!y) return x;
if (l == r) {
// 叶子区间,保留在该点处较小的线
if (eval(nodePool[x].line_id, l) <= eval(nodePool[y].line_id, l)) return x;
else return y;
}
int m = (l + r) >> 1;
nodePool[x].lson = mergeTrees(nodePool[x].lson, nodePool[y].lson, l, m);
nodePool[x].rson = mergeTrees(nodePool[x].rson, nodePool[y].rson, m + 1, r);
// 把 y 当前结点上驻留的线插入合并后的树(注意:update 会以线信息为主,并在需要时清空被挂上节点的子指针)
update(x, l, r, y);
return x;
}
// query:在以 cur 为根的李超树中查询 x=pos 的最小值
ll query(int cur, int l, int r, int pos) {
if (!cur) return INF;
ll res = eval(nodePool[cur].line_id, pos);
if (l == r) return res;
int m = (l + r) >> 1;
if (pos <= m) return min(res, query(nodePool[cur].lson, l, m, pos));
else return min(res, query(nodePool[cur].rson, m + 1, r, pos));
}
// DFS:计算 dp 值并维护每个节点对应的李超树
void dfs(int u, int parent) {
bool isLeaf = true;
for (int v : g[u]) if (v != parent) {
isLeaf = false;
dfs(v, u);
// 合并子树 v 到当前 u 的段树
root[u] = mergeTrees(root[u], root[v], 0, MAXW);
}
if (isLeaf) {
dp[u] = 0; // 叶子的 dp = 0
} else {
int pos = a[u] + BASE;
dp[u] = query(root[u], 0, MAXW, pos);
}
// 把当前结点 u 对应的线 y = b_u * x + dp[u] 插入当前树
rec[u].m = (ll)bval[u];
rec[u].c = dp[u];
++idtot;
nodePool[idtot].lson = nodePool[idtot].rson = 0;
nodePool[idtot].line_id = u; // 指向 rec[u]
update(root[u], 0, MAXW, idtot);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
for (int i = 1; i <= n; ++i) cin >> bval[i];
for (int i = 0; i < n - 1; ++i) {
int u, v; cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
idtot = 0;
for (int i = 1; i <= n; ++i) {
root[i] = 0;
nodePool[i].lson = nodePool[i].rson = 0;
}
dfs(1, 0);
for (int i = 1; i <= n; ++i) {
cout << dp[i];
if (i == n) cout << '\n';
else cout << ' ';
}
return 0;
}







 浙公网安备 33010602011771号
浙公网安备 33010602011771号