20250721 GF集训 构造
https://www.luogu.com.cn/problem/CF538G

发现我们给出的限制可以拆成一个区间加上若干倍整个序列和的形式,但是此时我们的 x,y 两维需要一起考虑,不是非常容易。考虑将坐标系旋转 45°,那么操作就会变为 (1,1),(1,−1),(−1,1),(−1,−1)
我们考虑将 t 时刻的横纵坐标都加上 t 再除以 2。
这样 ULDR 对应的就是 (1,1),(0,1),(0,0),(1,0),此时原来的 (xi,yi) 对应成 ((2xi+yi+t) / 1,(2yi−xi+t)/2)。
先判掉奇偶性不合法的情况,剩下的只用考虑距离上的约束。

https://www.luogu.com.cn/problem/P7320
一张 n 个点 m 条边的简单无向连通图。很快,他就被 ducati 和 b6e0 盯上了。
ducati 希望能够从中找到恰好 ⌈n/6⌉ 条不同的路径,使得所有的点都被至少一条路径经过。
b6e0 希望找到一个大小恰好为 ⌊n/3⌋ 的节点集合,使得它们之间两两没有边。
lnlhm 知道,如果他没有满足某个人的要求,那么他就会被揍。因此,他向你求助:是否存在一种选择边或点的方案,使得最多被一个人揍?
选择一个非叶子节点作为根,dfs树的叶子数量如果大于n/3,那么肯定是最大独立集。
否则叶子之间两两配对,寻找一种方案v[i], v[i + m2 / 2]配对,可以证明一定可以覆盖全部。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int nmax = 1005;
vector<int> e[nmax], v;
int n, m;
int fa[nmax], d[nmax], flg, vis[nmax], lf[nmax];
void dfs(int u, int f) {
int cnt = 0;
vis[u] = 1;
fa[u] = f;
d[u] = d[f] + 1;
for (int x : e[u]) {
if (vis[x]) continue;
cnt++;
dfs(x, u);
}
if (cnt == 0) {
v.push_back(u);
lf[u] = 1;
}
if (u == 1 && cnt == 1) flg = 1;
}
inline void pt(int x, int y) {
vector<int> l, r;
while (x != y) {
if (d[x] > d[y]) {
l.push_back(x);
x = fa[x];
} else {
r.push_back(y);
y = fa[y];
}
}
reverse(r.begin(), r.end());
cout << (int)(l.size() + r.size()) + 1 << " ";
for (int i : l) cout << i << " ";
cout << x << " ";
for (int i : r) cout << i << " ";
cout << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1, u, w; i <= m; i++) {
cin >> u >> w;
e[u].push_back(w);
e[w].push_back(u);
}
dfs(1, 0);
if ((int)v.size() >= n / 3) {
cout << "2\n";
for (int i = 0; i < n / 3; i++) cout << v[i] << " ";
cout << "\n";
} else {
cout << "1\n";
if (flg) {
v.push_back(1);
lf[1] = 1;
}
int m2 = (int)v.size();
int cnt = (n + 5) / 6;
for (int i = 0; i + m2 / 2 < m2 && cnt; i++) {
pt(v[i], v[i + m2 / 2]);
cnt--;
}
for (int i = 1; i <= n && cnt; i++) {
if (!lf[i]) {
pt(i, i);
cnt--;
}
}
}
return 0;
}
https://www.luogu.com.cn/problem/AT_arc103_d
给出 N 个互不相同的数 Di,表示树上的节点 i 到其他所有点的距离和。
请判断是否存在这样一棵树,其中每条边的长度均为 1。若存在请输出一种方案,否则输出 -1。
1≤N≤105,1≤Di≤1012。
这个题限制非常严格,与其说是构造,不如说是还原
如果从 u 变化到 v,那么相当于 u 左边的点对 Dv 的贡献比 Du 多 1,也就是做出了一个等于 size[u] 的贡献。而在 v 右边的点对 Dv 的贡献比 Du 少 1,也就是做出了一个等于 −size[v] 的贡献。

由于一个叶子的Di肯定是最大的,重心肯定最小的,所以找到这个最大的Di,找到他的父亲,如果二分不到就是无解,一步一步还原就行。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
constexpr int maxn = 1e5 + 10;
#define int long long // 保留
struct edge {
int to, next;
};
array<edge, maxn * 2> e; // FIX: 原来 *4,2*(n-1) 足够
array<int, maxn> head;
int edgecnt = 0;
void addedge(int u, int v) {
e[++edgecnt].to = v;
e[edgecnt].next = head[u];
head[u] = edgecnt;
}
pair<int, int> D[maxn];
pair<int, int> ans[maxn];
array<int, maxn> sz, dis;
int n, tot;
void dfs(int u, int fa) {
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
if (v == fa) continue;
dis[v] = dis[u] + 1;
dfs(v, u);
}
}
signed main() {
#ifdef OFLINE
freopen("in.in", "r", stdin);
freopen("out.ouw", "w", stdout);
#endif
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> D[i].first;
D[i].second = i;
sz[i] = 1;
}
sort(D + 1, D + n + 1, greater<pair<int, int>>());
for (int i = 1; i < n; i++) {
int u = D[i].second;
int delta = D[i].first - n + 2 * sz[u];
int l = 1, r = n, pos = 0;
while (l <= r) {
int mid = (l + r) >> 1;
if (D[mid].first <= delta) {
r = mid - 1;
pos = mid;
} else {
l = mid + 1;
}
}
if (pos == 0 || D[pos].first != delta) {
cout << -1 << endl;
return 0;
}
int v = D[pos].second;
addedge(u, v);
addedge(v, u);
ans[++tot] = {u, v};
sz[v] += sz[u];
}
dfs(D[n].second, 0);
int sum = 0;
for (int i = 1; i <= n; i++) sum += dis[i];
if (sum == D[n].first) {
for (int i = 1; i <= tot; i++) {
cout << ans[i].first << " " << ans[i].second << endl;
}
} else {
cout << -1 << endl;
}
return 0;
}
https://www.luogu.com.cn/problem/CF611H
https://www.luogu.com.cn/problem/CF1508D
给定平面上 n 个点,第 i 个点坐标为 (xi,yi) 点权为 ai,其中任意三点均不共线。
你可以执行以下操作若干次:
选择两个不同的下标 i,j,交换 ai,aj,然后以点 i 点 j 为两端点画出一条线段。
要求最终形成的图中不存在相交线段(交于端点处不认为相交,相同线段认为相交),并且满足 ai=i。
给出任意一种方案或者报告无解。
交换和不相交是分离的,关系几乎没有,引导我们分开考虑。
先考虑交换,如果在一个置换环上就做完了,如果不在,我们可以通过交换任意两个元素的标签的方式变成一个,用DSU维护。如果是一个置换环,那么交换后的图是一个菊花,那么合并置换环的操作就是连接菊花的一些花瓣。
但是只有在两个花瓣夹角小于180度的时候才有可能没有交点,所以我们选择一个边上的点,保证小于180度即可,按斜率排序,具体看代码:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2005;
int n, m;
array<int, N> pos;
vector<pair<int, int>> ans;
struct DSU {
array<int, N> fa;
void Init() {
for (int i = 1; i <= n; i++) {
fa[i] = i;
}
}
int Query(int p) {
if (fa[p] == p) return p;
return fa[p] = Query(fa[p]);
}
void Merge(int p, int q) {
fa[p] = q;
}
} dsu;
int pvtx, pvty, pvt;
struct point {
int x, y, a, id;
double agl;
bool operator < (const point &oth) const {
return agl < oth.agl;
}
};
array<point, N> p, q;
int main() {
#ifdef OFLINE
freopen("in.in", "r", stdin);
freopen("out.ouw", "w", stdout);
#endif
ios::sync_with_stdio(false);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> p[i].x >> p[i].y >> p[i].a;
p[i].id = i;
if (p[i].a != i) {
q[++m] = p[i];
}
}
if (!m) {
cout << "0\n";
return 0;
}
dsu.Init();
pvtx = q[1].x;
pvty = q[1].y;
pvt = 1;
for (int i = 2; i <= m; i++) {
if (q[i].x < pvtx) {
pvtx = q[i].x;
pvty = q[i].y;
pvt = i;
} else if (q[i].x == pvtx && q[i].y < pvty) {
pvty = q[i].y;
pvt = i;
}
}
if (pvt != 1) {
swap(q[1], q[pvt]);
}
for (int i = 2; i <= m; i++) {
q[i].agl = atan2(q[i].y - pvty, q[i].x - pvtx);
}
sort(q.begin() + 2, q.begin() + m + 1);
for (int i = 1; i <= m; i++) {
int u = dsu.Query(q[i].id);
int v = dsu.Query(q[i].a);
if (u != v) {
dsu.Merge(u, v);
}
}
for (int i = 2; i < m; i++) {
int u = dsu.Query(q[i].id);
int v = dsu.Query(q[i + 1].id);
if (u != v) {
ans.push_back({q[i].id, q[i + 1].id});
swap(q[i].a, q[i + 1].a);
dsu.Merge(u, v);
}
}
for (int i = 1; i <= m; i++) {
pos[q[i].id] = i;
}
while (q[1].a != q[1].id) {
int u = pos[q[1].a];
ans.push_back({q[1].id, q[u].id});
swap(q[1].a, q[u].a);
}
cout << ans.size() << endl;
for (auto &pr : ans) {
cout << pr.first << ' ' << pr.second << endl;
}
return 0;
}
https://www.luogu.com.cn/problem/CF741C
有2n个人围成一圈坐在桌子边上,每个人占据一个位子,对应这2n个人是n对情侣,要求情侣不能吃同一种食物,并且桌子上相邻的三个人的食物必须有两个人是不同的,只有两种食物(1或者是2),问一种可行分配方式。
二分图染色。
限制1直接连边即可。
限制2考虑隔一个连一个,即连接在环上i2-1和i2,这样可以证明一定是二分图,因为没有奇环,没有两个人是同一个老婆。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
constexpr int maxn = 2e5+10;
array<int,maxn> x, y, c;
struct edge{
int to,next;
};
array<edge,maxn * 2> e;
array<int,maxn> head;
int cnt;
void addedge(int u,int v){
e[++cnt].to = v;
e[cnt].next = head[u];
head[u] = cnt;
}
int n;
array<bool,maxn> vis;
void dfs(int x,int col){
vis[x] = true;
c[x] = col;
for(int i = head[x];i;i = e[i].next){
int v = e[i].to;
if(vis[v]) continue;
dfs(v, 3 - col);
}
}
int main(){
#ifdef OFLINE
freopen("in.in","r",stdin);
freopen("out.ouw","w",stdout);
#endif
cin>>n;
for(int i = 1;i <= n;i++){
cin>>x[i]>>y[i];
addedge(x[i],y[i]);
addedge(y[i],x[i]);
}
/*
v[i*2-1].push_back(i*2);
v[i*2].push_back(i*2-1);
*/
for(int i = 1;i <= n;i++){
addedge(i*2+1,i*2);
addedge(i*2,i*2+1);
}
for(int i = 1;i <= n * 2;i++){
if(!vis[i]) dfs(i,1);
}
for(int i = 1;i <= n;i++){
cout<<c[x[i]]<<" "<<c[y[i]]<<endl;
}
return 0;
}
https://www.luogu.com.cn/problem/AT_arc131_e
给定一个完全无向图,要求用 RGB 对每条边进行染色,使得三种颜色的边数一样,且不存在三个点使得对应的三条边颜色均不相同。
增量构造
当 n=6 时,分成 {1,4},{2,3},{5};
当 n=7 时,分成 {1,6},{2,5},{3,4};
当 n=9 时,分成 {1,2,3,6},{4,8},{5,7};
当 n=10 时,分成 {1,2,3,4,5},{6,9},{7,8};
当 n>10 时,考虑递推构造,把 [n−6,n−1] 首尾分成三组,然后转化为 n−6 的子问题。
https://www.luogu.com.cn/problem/CF1270E
给定 n≥2 个两两不同、坐标为整数的点。你的任务是将这些点划分为两个非空的集合 A 和 B,使得满足以下条件:
对于任意两点 P 和 Q,在黑板上写下它们之间的欧几里得距离:如果它们属于同一组,则用黄色笔写下;如果属于不同组,则用蓝色笔写下。要求所有黄色数字都不等于任何一个蓝色数字。
保证对于任意输入都存在这样的划分。如果存在多种划分方式,你可以输出其中任意一种。
奇妙的ADHOC
考虑国际象棋棋盘样式的染色,如果能把点划分为两个集合,那么黑白之间连黄色,同色之间连接蓝色,这样距离显然不会一样。
但是如果点全部落在黑色/白色呢?
考虑把棋盘旋转45度,他还是个棋盘。
(题解没有图我自己画一张)

红色是第一个棋盘,蓝色是递归生成的。
一直递归下去即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int n, x[N], y[N];
int s[N], ts;
vector<int> slove(){
int all_black = 1, all_white = 1;
for (int i = 1; i <= n; ++i) {
all_black &= !((x[i] + y[i]) & 1);
all_white &= (x[i] + y[i]) & 1;
}
if (!all_black && !all_white) {
vector<int> ans;
for (int i = 1; i <= n; ++i) {
if ((x[i] + y[i]) & 1) ans.push_back(i);
}
return ans;
}
if (all_white) {
for (int i = 1; i <= n; ++i) x[i]--;
}
for (int i = 1, x0, y0; i <= n; ++i) {
x0 = x[i];
y0 = y[i];
x[i] = (x0 + y0) >> 1;
y[i] = (x0 - y0) >> 1;
}
return slove();
}
int main() {
#ifdef OFLINE
freopen("in.in","r",stdin);
freopen("out.ouw","w",stdout);
#endif
cin>>n;
for (int i = 1; i <= n; ++i) {
cin>>x[i]>>y[i];
}
vector<int> ans = slove();
cout << ans.size()<<endl;
for(auto x : ans){
cout<<x<<" ";
}
cout<<endl;
return 0;
}
https://www.luogu.com.cn/problem/AT_agc027_d
构造一个 N×N 的矩阵. 要求:
所有元素互不相同.
满足 ai,j≤1015.
对于任意两个相邻的数字 ,max(x,y)modmin(x,y) 都相等,且均为正整数。
可以证明方案一定存在.
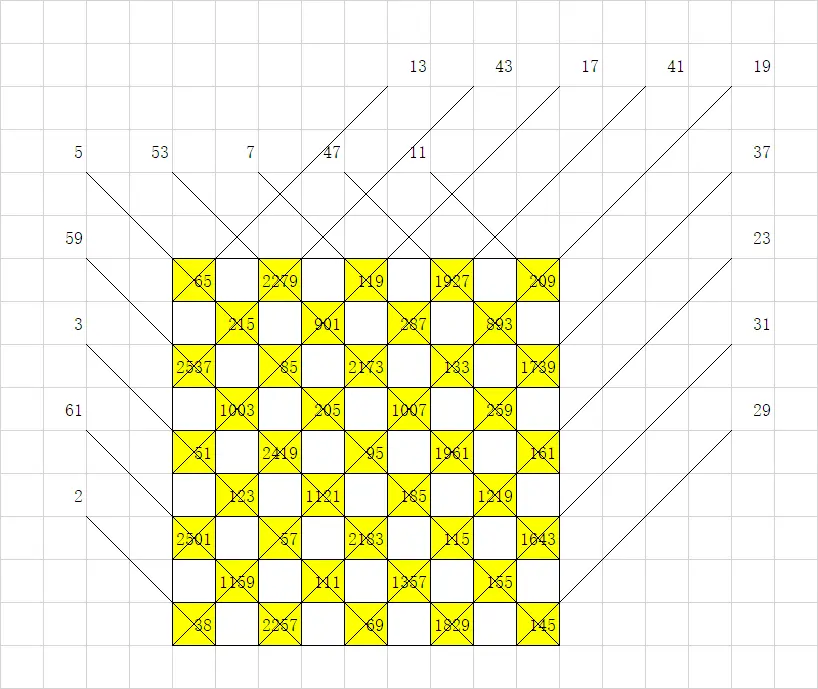
如图所示,黑白染色后,每个黑色格子按照每个正 / 反斜对角线填上两个质数的乘积。
令 m=1,则白色格子上的数为相邻四个黑色格子上的数的 lcm+1。
稍微调整一下质数的顺序,就可以做到数不超过 10^15 了
具体地,将质数分为前一半大和前一半小两种。
保证每一个乘积都是一个大的乘一个小的即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
vector<int> primes;
void getprime(int n) {
std::vector<bool> is_prime(n + 1, true);
is_prime[0] = is_prime[1] = false;
for (int p = 2; p * p <= n; ++p) {
if (is_prime[p]) {
for (int i = p * p; i <= n; i += p)
is_prime[i] = false;
}
}
for (int p = 2; p <= n; ++p) {
if (is_prime[p]) {
primes.push_back(p);
}
}
//return primes;
}
signed main() {
#ifdef OFLINE
freopen("in.in","r",stdin);
freopen("out.ouw","w",stdout);
#endif
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n;
cin >> n;
getprime(20000);
vector<long long> P(n);
vector<long long> PP(n);
for (int i = 0; i < n; ++i) {
P[i] = primes[i];
PP[i] = primes[n + i];
}
vector<vector<long long>> a(n, vector<long long>(n));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if ((i + j) % 2 == 0) {
int anti_diag_idx = (i + j) / 2;
int main_diag_idx = (i - j + n - 1) / 2;
a[i][j] = P[anti_diag_idx] * PP[main_diag_idx];
}
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if ((i + j) % 2 != 0) {
int anti_diag_idx1 = (i + j - 1) / 2;
int anti_diag_idx2 = (i + j + 1) / 2;
int main_diag_idx1 = (i - j - 1 + n - 1) / 2;
int main_diag_idx2 = (i - j + 1 + n - 1) / 2;
long long lcm = P[anti_diag_idx1] * P[anti_diag_idx2] *
PP[main_diag_idx1] * PP[main_diag_idx2];
a[i][j] = lcm + 1;
}
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cout << a[i][j] << (j == n - 1 ? "" : " ");
}
cout << "\n";
}
return 0;
}
给定一个 n×m 的矩阵 A , 保证 A 内的元素为 1 到 n×m 的排列.
将 A 每一行的元素任意排列得到 B .
将 B 每一列的元素任意排列得到 C .
将 C 每一行的元素任意排列得到 D .
要求 Di,j=(i−1)×m+j , 请输出一组合法的 B,C.
每一行最后目标元素各个染色,
要求排列每一行,使得每列包含恰好 n 种颜色。
每行建立一个节点,每个颜色建立一个节点,每行向包含的每个颜色连包含次数条边。
这个二分图的一个完美匹配对应了一列的方案,只需要跑 m 次就可以得到 B 矩阵。
问题是怎么证明这个图一定扛得住 m 个完美匹配。
还剩 k 列没选择的时候,这张图是一张 k-正则 二分图,根据 Hall 定理的推论,一定存在完美匹配。






 浙公网安备 33010602011771号
浙公网安备 33010602011771号