20250717 计数

P11363 [NOIP2024] 树的遍历

k=1

我们已经知道是从那条边开始了，每一个点的过程就是从一条边来，以任意顺序，以一条链的形态走完自己后续的边，顺便访问自己子树的情况，答案就是：
∏(di​−1)!

---

什么情况会生成相同的树？

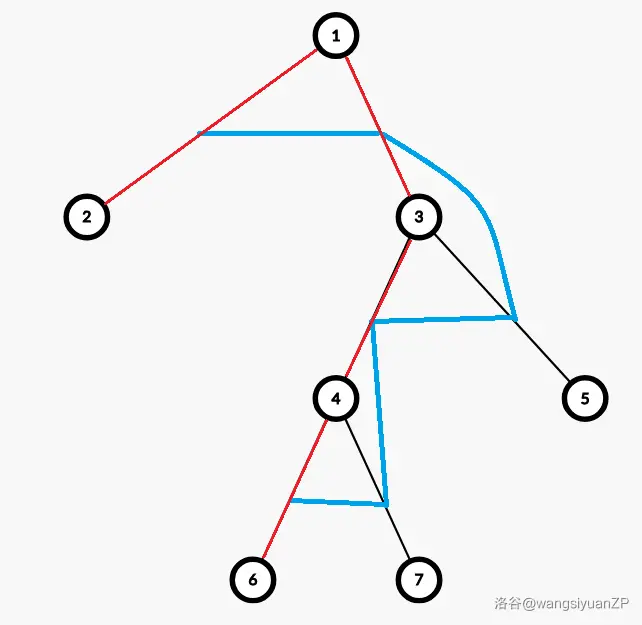
可能的根节点一定恰好是一条从原树的叶子到叶子的链。

有一棵树，边有 0/1 权值，点有点权，求所有叶子到叶子的链，满足这条链上有一条 1 边，点权的乘积的和是多少。

树形dp, fu,0/1 u的子树内叶子到他有没有1的乘积和

---

P3702 [SDOI2017] 序列计数

Alice 想要得到一个长度为 n 的序列，序列中的数都是不超过 m 的正整数，而且这 n 个数的和是 p 的倍数。

Alice 还希望，这 n 个数中，至少有一个数是质数。

Alice 想知道，有多少个序列满足她的要求。

---

考虑熔池

全部的减去没有质数的

全部的，

cnti​表示1∼m中modP为i的个数
令fi,j​表示i个数modp等于j的方案数

然后如果要求没有质数的，把cnt变成这样

cntx​=i∈[1..m]∑​[imodp=x∧is_not_prime(i)]

即可

---

P6008 [USACO20JAN] Cave Paintings P

Bessie 成为了一名艺术家，正在创作壁画！她现在正在创作的作品是一个高为 N 的方阵，方阵的每行都由 M 个方格组成（1≤N,M≤1000）。每个方格是空的，画了石头，或者画了水。Bessie 已经画上了包含石头的方格，包括整幅画作的边界。她现在想要将某些空的方格画上水，使得如果这幅画是真实的，其中应当不存在水的净移动。定义从上到下第 i 行的方格的高度为 N+1−i。Bessie 想要她的画作满足以下限制：

假设方格 a 画的是水。那么如果存在一条从 a 到方格 b 的路径，由高度不超过 a 的空的方格或是有水的方格组成，路径中每相邻两个方格都有一条公共边，那么 b 画的也是水。

求 Bessie 可以创作的不同作品的数量模 109+7 的余数。Bessie 可以将任意数量的空格画上水，包括不画以及全画。

---

发现答案可以乘法原理。

所以从下往上维护连通块，高度一点点增加，显然会发生合并，用并查集维护，merge的时候乘起来即可。

记得最后把没有合并的乘起来

---

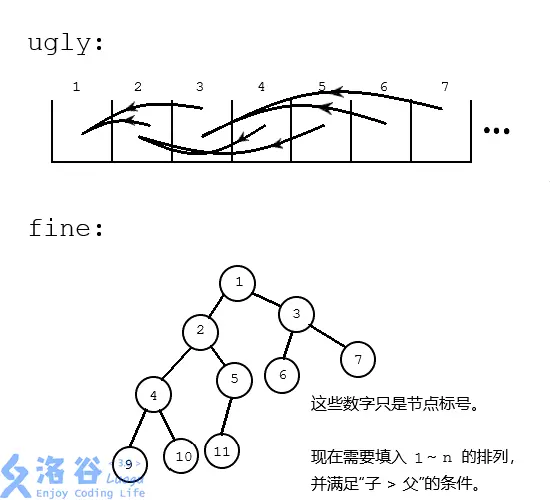
P2606 [ZJOI2010] 排列计数

称一个 1∼n 的排列 p1​,p2​,…,pn​ 是 Magic 的，当且仅当
∀i∈[2,n],pi​>p⌊i/2⌋​

计算 1∼n 的排列中有多少是 Magic 的，答案可能很大，只能输出模 m 以后的值。

---

用一个套路

把二叉树建出来

发现左子树和右子树互不影响

直接相乘

C(n - 1, L) × 左子树填满并满足小根堆性质的方案数 × 右子树填满并满足小根堆性质的方案数。

---

P5664 [CSP-S2019] Emiya 家今天的饭

具体地

我们希望一个矩阵

每一行最多选一个

每一列最多选半数个/

容斥计算：每行选不超过一个的方案数 - 每行选不超过一个，且某一列选了超过一半的方案数。

那么考虑枚举不合法的一列。假设我们已经枚举了不合法的列为col，接下来会发现我们只关心一个数的位置是否在当前列；如果属于在其他列的情况，那么它具体在哪一列对当前列的合法性并无影响，我们并不需要考虑。

接下来设计状态。fi,j,k​表示对于col这一列，前i行在col列中选了j个，在其他列中选了k个，那么令si​为第i行的总和，则有转移：
fi,j,k​=fi−1,j,k​ + ai,col​∗fi−1,j−1,k​ + (si​−ai,col​)∗fi−1,j,k−1​

---

但是复杂度会爆炸，考虑i和j其实不重要，重要的是他们的差

所以只考虑当前i行，当前列的数比其他列的数多了j个

fi,j​=fi−1,j​ + ai,col​∗fi−1,j−1​ + (si​−ai,col​)∗fi−1,j+1​

---