20250715 模拟赛 总结

T1

题目描述

众所周知，YC乌龙 切题就像切小菜，他的同学 crimson000 担心他的身体状况，奉劝 YC乌龙 不要再卷了，没想到 YC乌龙 说：“我就不休息能把我咋的，我卷死你。” 秉持着卷不过就加入的原则，crimson000 决定和他一起切题 (?)。

现在 Johnsonloy 有 nn 道题给他们两个人做，第 ii 道题有一个难度系数 aiai​，一个题只能被切一次。crimson000 和 YC乌龙 轮流行动，crimson000 先手。每次行动 crimson000 需要切掉至少一道题，YC乌龙 需要切掉恰好一道题，直到所有题都被切完。

每个人最终的得分是自己切掉的题的难度系数之和。为了让 YC乌龙 少卷一点，crimson000 想最大化自己的得分，然而 YC乌龙 也想最大化自己的得分。请你告诉 crimson000，他最终能得多少分呢？
输入格式

从标准输入读入数据。

第一行一个正整数 nn 。

第二行包含 nn 个整数，第 ii 个整数表示 aiai​ 。
输出格式

输出到标准输出。

一行一个整数，表示 crimson000 的最终得分。
样例输入1

5
7 10 -5 -2 -4

样例输出1

13

样例解释1

切题的过程如下：

crimson000 切掉 {7,10}{7,10}

YC乌龙 切掉 −2−2

crimson000 切掉 {−4}{−4}

YC乌龙 切掉 −5−5

crimson000 的得分为 7+10+(−4)=137+10+(−4)=13

---

YC乌龙 的策略总是选择当前剩余的最大数

crimson000 只会在第一步选择超过一个数

将所有数字排序后 crimson000 第一步一定选择一段前缀

枚举这个前缀，后面的部分是两个人轮流取最大数，这个过程可以前缀和优化快速计算。

复杂度瓶颈在排序 O(nlog⁡n)O(nlogn)。

---

T 2

题目描述

众所周知 YC乌龙 会后空翻，甚至会在序列上进行后空翻

给定两个只包含 0、1 的长度为 nn 的序列 S,TS,T，YC乌龙在序列 SS 上可以进行后空翻，同时带动一个区间翻转

你每次可以选择一个区间 l,rl,r 来让 YC乌龙进行后空翻，你需要保证 ∑i=lr[Si=1]∑i=lr​[Si​=1] 是偶数。

要求进行少于 8n8n 次操作，使得 SS 和 TT 最终相等。你需要判断无解。
输入格式

第一行一个字符串表示 SS。

第二行一个和 SS 长度相同的字符表示 TT。
输出格式

假如无解，则输出 NO。

假如有解，第一行输出 YES，第二行输出一个数 mm 表示你使用的操作次数，接下来 mm 行，每行两个数表示你选择操作的 l,rl,r。
数据范围

对于 20%20% 的数据，保证 n≤16n≤16。

对于 40%40% 的数据，保证 n≤100n≤100。

对于 60%60% 的数据，保证 n≤1000n≤1000。

对于 100%100% 的数据，1≤n≤100001≤n≤10000。

---

两种做法，但是我赛时使用了

下标从0开始输出

挂成0了

---

1. hdkk做法 考虑使用反转将S和T排序

如果排序后，S和T相等，就有解，构造方案就是S的排序操作和反转后的T的排序操作。

2. 赛时认为是假的 但是被tianzekai证明了是对的

考虑从左往右构造每一位，显然去后面找数换

我以为如果找不到需要随机化什么的

实际上找不到就直接No了

因为操作可逆

---

T3

题目描述

AliceAlice 和 BobBob 是一对好朋友，他们特别喜欢玩飞行棋

但是日复一日玩经典的游戏让他们觉得有些无聊

所以他们修改了飞行棋的规则：

在一个长度为 nn 的棋盘上，AliceAlice 先手，落在1号节点并且使矿山金币减一

两人可以自由选择自己前进的步数，但是不能超过范围 mm，也可以原地踏步

在两人的路上有一些矿山，位置为 ii 的矿山上有 aiai​ 的金币可以发掘

每次行动，当前人必须前进若干步（也可原地踏步）至一个有金币的矿山上，然后在到达的位置上进行开采，得到一个金币

如果到了一个人的回合，而那个人不能走到任何一个有金币的矿山，则落败

他们的好朋友兼裁判聪聪觉得这是一个简单的游戏，想要加大一些难度，并且知道谁能获胜，他会进行两种操作：

向一个区间内的矿山上各放上 xx 个金币
询问 AliceAlice 和 BobBob 在将一个区间单独拿出来进行游戏时谁能够获胜（每次询问独立）

输入格式

第一行三个整数 n,m,qn,m,q 表示棋盘的长度，每一次能前进的最大步数，询问次数

第二行 nn 个正整数 aiai​ 表示每个位置的棋子个数

接下来 qq 行，每行第一个整数 opop 表示操作类型，若 op=1op=1，接下来输入三个整数 l,r,v,1≤l≤r≤n,1≤v≤1012l,r,v,1≤l≤r≤n,1≤v≤1012 表示将区间 [l,r][l,r] 内的 aiai​ 各加上 vv，若 op=2op=2，接下来两个整数 l,r(1≤l≤r≤n)l,r(1≤l≤r≤n) 表示询问

---

被唐诗题面坑了，好在我同时看错了先后手导致仍然有16分

---

nq：

如果当前位置能够走到一个先手必败的位置，就直接走过去，如果走不到一个先手必败的位置就进行原地踏步

那么先手原地踏步，后手也一定会跟着原地踏步

那么如果当前的棋子个数是奇数则先手必胜，否则先手必败，因为取到不能取一定是后手（在走不到一个先手必胜的位置上时）

那就可以发现一个位置的金币个数是没有用的，有用的只有他的奇偶性

那么我们就可以先将每一个位置mod  2mod2

考虑 Subtask2Subtask2的数据范围一看就是给 O(nq)O(nq) 过的，那么我们考虑直接把这个区间拿出来做

我们考虑从后往前 dpdp ，设 fifi​ 表示如果先手在 ii 位置能否获胜

那么如果当前位置的棋子是奇数， fi=1fi​=1，否则如果在后面 mm 个位置有先手必败态则为 11，否则为 00

我们只需要查看开头的 dpdp 值是多少即可

我们发现如果一个人现在后面有很多个必败态可以走，只需要走其中任何一个就可以胜利，那么我们直接维护 [r+1,r+m][r+1,r+m] 里面最靠左的 dpdp 值是 00 的位置即可，不难发现可以像上面一样合并并且复杂度是 O(m)O(m)，所以总复杂度就是 O(qmlog⁡n)O(qmlogn)

---

T4

---

考虑用这种构造方法：

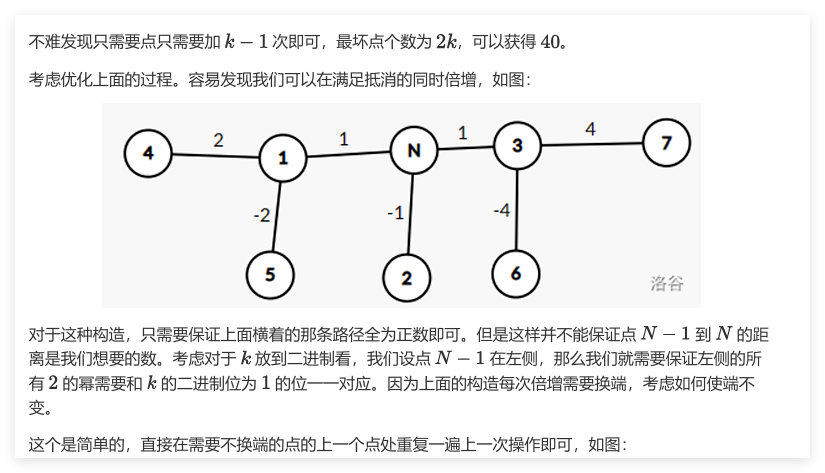
钦定k是奇数。

我们发现每次加入一对点，边权值都会mul 2

这样可以保证约束是0

但是

n-1 到 n最后加入一个单个的，无法保证

所以我们考虑二进制拆分

用正的二进制边权让这条边恰好等于k就可以了

至于如何让k变成奇数？

除以2就可以了

除以2之后只需要这样更改： 把k一直除以2,除以到一个2的次幂，边权在x一个2的次幂

---