20250710 杂题
P5512 [NOIP 1997 提高组] 棋盘问题 加强版
在 N×N(1≤N≤10)的棋盘上,填入 1,2,…,N2 共 N2 个数,使得任意两个相邻的数之和为素数。
直接暴搜搜到4就轧钢了,预处理素数可以搜到6.
考虑减脂
因为要要求第一行和第一列最小并且左上角一定是1,所以优先枚举这部分,并且维护最小合法值,后面慢慢填,预处理出两个数都合法的情况可以让你的复杂度降一个n,此时打表已经可以通过。
但是需要更快?
我们可以玄学行列交替搜索,避免刚开始搜索时,较小的数字大部分处于数组上部,较大的数字被迫在数组下部搜索,我们知道,较大的数字中质数分布是较少的,所以让小数字与大数字匹配更优,反正我们已经保证了第一行第一列是用较小的数字搜的,其他位置是没有必要控制大小的。行列交替搜索使得大小数字较均匀分布,更易搜出最优解
然后考虑如何转化成任意解问题,显然,当当前解已经达到了最优解的下限时,我们就可以直接输出了
我们首先可以找到一个最优解的下限(2n−1)n,那就是第一行第一列取遍1∼2n−1的情况,此时已经没有更优解了
实际上,在n为偶数时,我们可以提高下限
为什么呢?
首先,1∼2n−1有n个奇数和n−1个偶数
为了保证相邻的x,y和为质数,由于x+y>2,x+y为奇数,所以所有的(x,y)都是一奇一偶的,那么第一行奇偶交错,有2n个奇数和2n个偶数,同样第一列也奇偶交错,有2n个奇数和2n个偶数
由于(1,1)位置的数1被重复计算两次,最终第一行第一列共有n−1个奇数和n个偶数,矛盾了
所以下限被提高到(2n−1)n+1,搜到直接退出即可
如果搜不到,那就回去暴搜。
P7115 [NOIP2020] 移球游戏
小 C 正在玩一个移球游戏,他面前有 n+1 根柱子,柱子从 1∼n+1 编号,其中 1 号柱子、2 号柱子、……、n 号柱子上各有 m 个球,它们自底向上放置在柱子上,n+1 号柱子上初始时没有球。这 n×m 个球共有 n 种颜色,每种颜色的球各 m 个。
初始时一根柱子上的球可能是五颜六色的,而小 C 的任务是将所有同种颜色的球移到同一根柱子上,这是唯一的目标,而每种颜色的球最后放置在哪根柱子则没有限制。
小 C 可以通过若干次操作完成这个目标,一次操作能将一个球从一根柱子移到另一根柱子上。更具体地,将 x 号柱子上的球移动到 y 号柱子上的要求为:
x 号柱子上至少有一个球;
y 号柱子上至多有 m−1 个球;
只能将 x 号柱子最上方的球移到 y 号柱子的最上方。
小 C 的目标并不难完成,因此他决定给自己加加难度:在完成目标的基础上,使用的操作次数不能超过 820000。换句话说,小 C 需要使用至多 820000 次操作完成目标。
我们考虑一个数,一个数的处理。
比如现在我们要把所有1放到一个柱子上,其他的我们不管。
朴素的思路,我们显然可以利用空柱,将一个柱子里所有的两类数分离,这样的操作复杂度是:
先随便挑一根柱子,把他一半砍到空柱子,这样你就得到了两根半满柱子,然后再分类即可。
需要,初始化200, 分类400,放回400,复原200,总共1200,你对每一根柱子都全部提出来,对于第一次n,总共需要50 * 1200次操作,然后就可以直接把所有最顶端的符合要求的放到空柱子上,代价400,然后要弄一颗新的空柱子,我们随便挑一个倒霉蛋把他分摊到其他空位即可,这个可以启发式做到小于400,我们就钦定他是400.所以处理一个当前还有n没有操作的方案,需要n * 1200 +800,总共是n是1到n的全部求和,1570000! 会轧钢。但是有一个很奇怪的地方,这玩意正好是答案的两倍,其实此时你已经有50分了。
但是你需要挑一个地方除一个2才行,怎么办?
我们发现复原的200和初始化的200很奇怪。
我们发现一旦有了一个和当前处理的这个数字无关的柱子,也就是说上面所有数都无关,那我们就不需要每次初始化复原了,只需要一开始初始化,最后复原即可,中间只需要类似扫描线离线处理的思路保证两个柱子长度即可。我们一开始做,然后一旦有一个无关柱子,我们501200就可以变成50800+400,其实你可以把后面400也省掉,因为你构造出来一个纯净柱子之后,你就再也不用放回他了,所以答案变成了n*800+1000,107000! 还是轧钢!
我们都用那种思想动态调试两个中间半柱的高度了,我们发现,如果我们把0取完不用放回该多好? 这样的话新的空串就出现了,然后你再把0的那一个部分回填回去。回填复杂度那不就退化了吗?其实不是,因为你需要分得1最多只有m个,只需要一点手法(细节不讲),就可以做到50 * 400 + 1400(我搜算乱了,但是不影响),大概在600000左右,轻松通过。
记得特判n = 2, n = 2你分不出来。
P8866 [NOIP2022] 喵了个喵
小 E 喜欢上了一款叫做《喵了个喵》的游戏。这个游戏有一个牌堆和 n 个可以从栈底删除元素的栈,任务是要通过游戏规则将所有的卡牌消去。开始时牌堆中有 m 张卡牌,从上到下的图案分别是 a1,a2,…,am。所有的卡牌一共有 k 种图案,从 1 到 k 编号。牌堆中每一种图案的卡牌都有偶数张。开始时所有的栈都是空的。这个游戏有两种操作:
选择一个栈,将牌堆顶上的卡牌放入栈的顶部。如果这么操作后,这个栈最上方的两张牌有相同的图案,则会自动将这两张牌消去。
选择两个不同的栈,如果这两个栈栈底的卡牌有相同的图案,则可以将这两张牌消去,原来在栈底上方的卡牌会成为新的栈底。如果不同,则什么也不会做。
这个游戏一共有 T 关,小 E 一直无法通关。请你帮小 E 设计一下游戏方案,即对于游戏的每一关,给出相应的操作序列使得小 E 可以把所有的卡牌消去。
构造题!
数据范围
很! 重! 要!
| 300 | 2n−1 |
2n-1啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
先看部分分,k=2n−2
考虑将数字 2i−1 和 2i 分配到第 i 个栈中,第 n 个栈就可以作为空辅助栈了。稍作思考可以给出以下的解法:
遇到一个数字 x,我们查看这个数字所分配到栈 s 的情况:
如果 s 为空,直接入栈;
如果 s 有 1 个元素,和 x 相同,将 x 入栈 s 并将这两个 x 消除;
如果 s 有 1 个元素,和 x 不同,将 x 入栈 s ;
如果 s 有 2 个元素,栈顶和 x 相同,将 x 入栈 s 并将这两个 x 消除;
如果 s 有 2 个元素,栈顶和 x 不同,那么栈底一定和 x 相同。将 x 入辅助栈 n,对栈 n 和栈 s 栈底相消。
容易看出,我们第偶数次遇到 x 的时候,总能立刻将它和上一个 x 抵消,所以一定能报告出解。
然后在多1呢? 就有点难搞了。
抛开栈 i 和数字 2i,2i−1 的绑定关系,采用先来后到的思想,按照 k=2n−2 的策略尽可能走下去。具体来说:
如果我们当前遇到的数 x 在所有栈中还没出现过,就把 x 射入一个还没满两个元素的栈,但如果已经有 n−1 个栈全都满了,说明我们按照 k=2n−2 的策略已经走不下去了(我们必须留一个空栈作为辅助栈,用来栈底相消)。
如果 x 在某个栈中出现了,直接使用 k=2n−2 的策略直接让当前的 x 和栈中出现的那个 x 消除。
当走不下去的时候,一定是局面上的 n−1 个栈全部被填满各两个元素,每种元素恰出现一次,且接下来要填的数还是一个没有在这 n−1 个栈中出现过的数 P。
直接把 P 放到辅助栈显然是错的:假如 P 后面跟了一个被压在栈底的数字,那么这两个数字可能很难再抵消,很不优。
我们考虑离线:也就是说,我们开始预知这个数后面都是什么数。依据后面数的情况,我们考虑 P 放在哪里。
考虑紧跟在 P 后方最长的一串数,满足这些数都在栈顶。如果不考虑当前 P 的去向,那么直接将这些数放到对应的栈,和栈顶相消即可,如果再来就仍然放置原来的栈顶。比如 5 是某个栈的栈顶,如果 P 后面来了个 5 就让它和 5 相消,如果再来一个 5 就放在原来的栈顶,如果再来就继续相消。因此我们发现,这些数还是相当自由的,我暂且称之为自由相消。
因此发现,如果 P 后面第一个不在栈顶上的数是 P,那么我们就把当前的 P 放入辅助栈,然后接下来的数自由相消,最后在第二个 P 来时,将它也放入辅助栈,栈顶相消即可。这种情况比较简单。
现在讨论 P 后面第一个不在栈顶上的数是一个栈底 X 的情况。我们记其对应栈为 S。此时未来的数列是 (P,⋯,X),其中 ⋯ 都是某个栈的栈顶。我们讨论 S 当前的栈顶 Y。
如果未来数列的 P 和 X 之间,Y 出现了奇数次:把 P 放入辅助栈,接下来一直自由相消,直到将处理 X 为止。由于 Y 的数量是奇数,加上一开始的一个 Y,此时 Y 一定被消除光,现在 S 的栈顶变成 X,将 X 放入 S 栈顶相消,S 变成了空栈。
如果 Y 出现了偶数次:把 P 放入 S,未来所有不为 Y 的栈顶自由相消,对于 Y,我们将其全部放入辅助栈相消,直到将处理 X 为止。由于 Y 的数量是偶数,这些 Y 一定都被消除光,辅助栈仍为空,我们将 X 放入辅助栈,和 S 栈底相消,辅助栈仍为空。
P9871 [NOIP2023] 天天爱打卡
奇怪的DP
小 T 同学非常热衷于跑步。为了让跑步更加有趣,他决定制作一款叫做《天天爱打卡》的软件,使得用户每天都可以进行跑步打卡。
开发完成后,小 T 同学计划进行试运行,他找了大 Y 同学来帮忙。试运行共 n 天,编号为从 1 到 n。
对大 Y 同学来说,如果某天他选择跑步打卡,那么他的能量值会减少 d。初始时,他的能量值是 0,并且试运行期间他的能量值可以是负数。
而且大 Y 不会连续跑步打卡超过 k 天;即不能存在 1≤x≤n−k,使得他在第 x 到第 x+k 天均进行了跑步打卡。
小 T 同学在软件中设计了 m 个挑战,第 i(1≤i≤m)个挑战可以用三个正整数 (xi,yi,vi) 描述,表示如果在第 xi 天时,用户已经连续跑步打卡至少 yi 天(即第 xi−yi+1 到第 xi 天均完成了跑步打卡),那么小 T 同学就会请用户吃饭,从而使用户的能量值提高 vi。
现在大 Y 想知道,在软件试运行的 n 天结束后,他的能量值最高可以达到多少?
感谢Copilot老师(bushi)
一个自然的 DP 状态是:\(dp[i]\) 表示在第 \(i\) 天结束时,能获得的最大能量值。
为了计算 \(dp[i]\),我们需要考虑第 \(i\) 天的决策:
-
决策一:第 \(i\) 天不跑步。
这种情况下,第 \(i\) 天没有能量变化,最大能量值继承自前一天。即 \(dp[i] = dp[i-1]\)。 -
决策二:第 \(i\) 天跑步。
这种情况比较复杂。如果第 \(i\) 天跑步,那么这一天必然是一段连续跑步区间的结束点。假设这段连续跑步区间从第 \(j\) 天开始,到第 \(i\) 天结束(\([j, i]\))。- 约束条件:
- 连续跑步天数不能超过 \(k\),所以 \(i - j + 1 \\le k\)。
- 既然从第 \(j\) 天开始连续跑,那么第 \(j-1\) 天必须是休息日。
- 能量计算:
- 初始能量:我们从第 \(j-1\) 天的休息状态转移而来。因此,在开始这段跑步前,我们的最大能量是在第 \(j-2\) 天结束时取得的,即 \(dp[j-2]\)。(如果 \(j=1\),则初始能量为 0)。
- 跑步消耗:从第 \(j\) 天到第 \(i\) 天,共跑了 \(i-j+1\) 天,消耗能量 \((i-j+1) \\times d\)。
- 挑战奖励:获得所有起始点不早于 \(j\)、结束点不晚于 \(i\) 的挑战奖励之和。我们记为 \(W(j, i)\)。
- 状态转移方程:
综合以上,对于一个从 \(j\) 到 \(i\) 的跑步区间,最终能量为 \(dp[j-2] - (i-j+1)d + W(j,i)\)。我们需要枚举所有可能的起点 \(j\) 来找到最大值。
- 约束条件:
结合两种决策,最终的转移方程为:
15分
然后你离散化,就是30分,现在dp[i] 表示在第 b_i 天结束时,能获得的最大能量值。
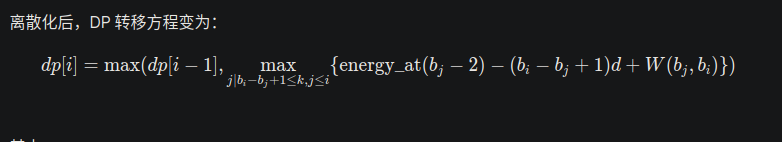
energy_at(t) 表示第 t 天结束时的最大能量,可以通过查询已计算出的 dp 数组得到。W(b_j,b_i) 是所有完整包含在 [b_j,b_i] 内的挑战奖励和。
这个转移的核心是枚举起点 j 来求最大值,这仍然很慢。我们需要优化这个过程。
我们将要求最大值的表达式进行变形:
energy_at(bj−2)−(bi−bj+1)d+W(bj,bi)=(energy_at(bj−2)+bjd+W(bj,bi))−bid−d
对于固定的终点 i,我们需要在所有合法的 j 中,最大化下面这个式子:
V(i,j)=energy_at(bj−2)+bjd+W(bj,bi)
换句话说
总能量 = (在 j-2 天结束时的能量) - (跑步成本) + (挑战奖励)
总能量 = ( (在 j-2 天的能量) + jd ) + (挑战奖励) - id - d
注意看,为什么要这么变换,这是一个套路,因为前面和j有关。
( (在 j-2 天的能量) + j*d ): 这部分只和起点 j 有关。我们称它为“起点基础值”。它代表了选择在 j 天开始跑步的初始潜力。
(挑战奖励): 这部分由线段树的区间增加操作来处理。
- i*d - d: 这部分只和终点 i 有关,可以在从线段树查出最大值后,最后再减去。
初始化 dp 数组,dp[0] = 0。
建立一个线段树,覆盖下标 1 到 p,所有初始值设为负无穷。线段树支持区间加和区间求最大值。
循环 i 从 1 到 p:
a. 决策一(不跑):dp[i] 首先可以从 dp[i−1] 继承,即 dp[i]=dp[i−1]。
b. 决策二(跑)准备:
i. 设置起点信息:对于将 b_i 作为跑步起点的方案,其前置状态是第 b_i−2 天的能量。通过二分查找在 b 数组中找到下标 k 使得 \(b\_k \\le b\_i-2 \< b\_{k+1}\),则前置能量为 dp[k]。将值 dp[k] + b[i] * d 更新到线段树的第 i 个位置上。这个值代表了选择 b_i 作为起点的基础价值。
ii. 更新挑战奖励:遍历所有结束点为 b_i 的挑战。对于每个挑战 (l_idx, v)(l_idx 是其起点的离散化下标),在线段树上对区间 [1, l_idx] 统一增加 v。这是因为任何在 l_idx 或更早位置开始的跑步,只要能覆盖到这个挑战,都能获得该奖励。
c. 决策二(跑)执行:
i. 查询最优起点:确定合法的最早起点。根据约束 b_i−b_j+1lek,有 b_jgeb_i−k+1。二分查找到满足此条件的最小下标 j_min。
ii.在线段树的 [j_min, i] 区间内查询最大值 M。这个 M 就是我们前面推导的 V(i,j) 的最大值。
iii.计算跑步方案的最终能量:M - b[i] * d。
d. 更新DP值:dp[i] = max(dp[i], M - b[i] * d)。
P2056 [ZJOI2007] 捉迷藏
这里只写括号序列做法。
转为括号序列,答案就变成了最远的两个黑点之间的未匹配括号数量。
用线段树维护,很复杂。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号