2-SAT + 网络流
Riddle
Description
nn 个点 mm 条边的无向图被分成 kk 个部分。每个部分包含一些点。
请选择一些关键点,使得每个部分恰有一个关键点,且每条边至少有一个端点是关键点。
Input
第一行三个整数 n,m,kn,m,k。
接下来 mm 行,每行两个整数 a,ba,b,表示有一条 a,ba,b 间的边。
接下来 kk 行,每行第一个整数为 ww,表示这个部分有 ww 个点;接下来 ww 个整数,为在这个部分中的点的编号。
朴素解法:
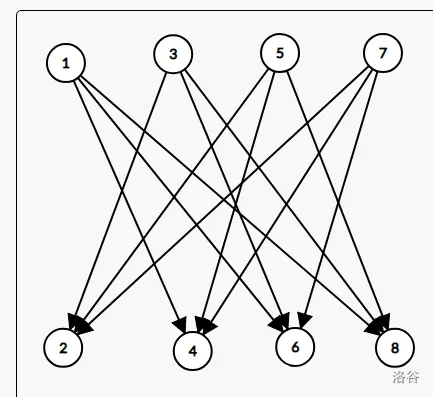

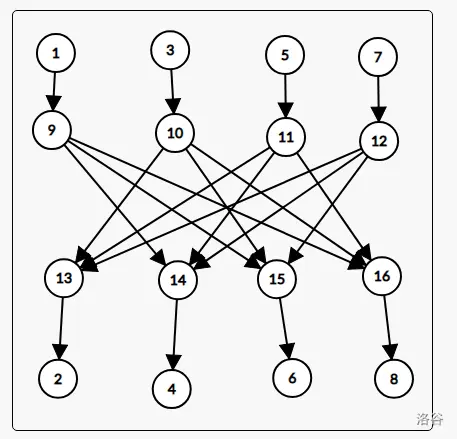
我们用类似前缀和优化建图,但是错了
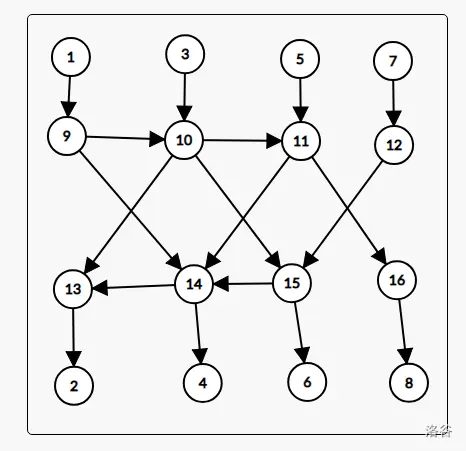
修复
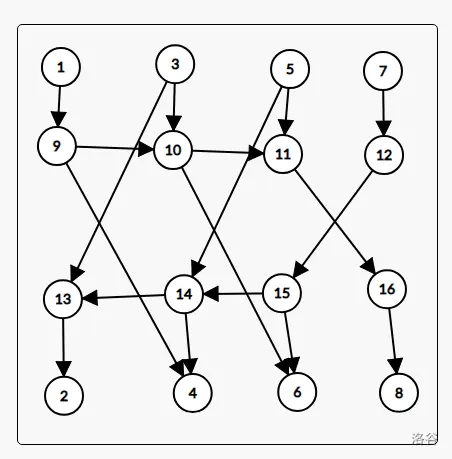
微调
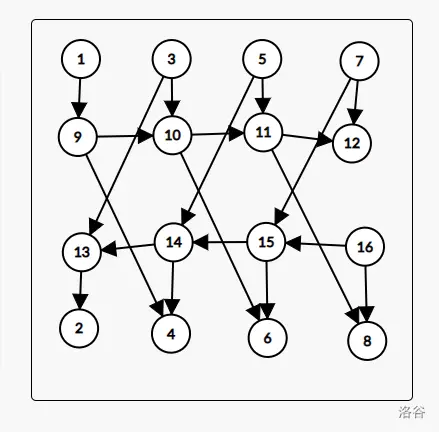
平面图判定
不难发现,除了哈密顿没有 其他东西了,之可能是一个大环外挂或者内缩。
我们发现两个同时在内侧/外侧的点,l1 < r1 < l2 < r2就会冲突,所以相交的线段不能在同一侧。
就可直接跑2SAT了
又很优美的n log n建边,但是我选择暴力
游戏
3SAT过的图灵奖选手(bushi)
考虑没有*的情况
对于一条限制 from to
如果from是禁止的,限制没有意义。
如果from是合适的,但是to是禁止的,那么from cur就不能选from.
如果from和to都是合适的,那么from选了要求的to也必须选要求的,如果to没有选要求的那么from就也不能选要求的。
然后这是2-SAT
但是有*
我们发现暴力枚举*是abc然后判断会爆炸
但是仔细想一想, *为a/b就一定有解了。
因为你每一个点最终用到的只是一辆车。
所以你如果不适合a,覆盖了bc,如果不适合b,覆盖了ac,都覆盖了。
最后在讲如何算方案。
vector<bool> get_solution() {
vector<bool> result(var_count + 1);
for (int i = 1; i <= var_count; i++) {
// 拓扑序更大的SCC对应的布尔值为真
result[i] = (belong[i] > belong[i + var_count]);
}
return result;
}
为什么这样赋值是正确的?
后访问完成的SCC获得更大的编号,这意味着在拓扑排序中位置更靠前
拓扑序更小的会推出更大的,但是反之不会
如果 belong[x] > belong[¬x],则在逆拓扑序中,x的SCC在¬x的SCC之前
这意味着如果我们从¬x出发,无法到达x(否则它们在同一SCC中)
但可能从x到达¬x
当 belong[x] > belong[¬x] 时,令 x = true
此时如果存在路径 x → ¬x,由于x为真,¬x也必须为真(但¬x代表x为假),这看似矛盾
但关键是:我们选择让 x = true,那么所有从x可达的节点都必须为真才能满足约束
由于¬x与x不在同一SCC,设置x=true不会强制¬x=true,因此没有矛盾
实际例子
假设有约束:x₁ ∨ x₂(至少一个为真)
转化为蕴含关系:
¬x₁ → x₂
¬x₂ → x₁
如果Tarjan算法得到:
belong[x₁] = 2, belong[¬x₁] = 1
belong[x₂] = 1, belong[¬x₂] = 2
则赋值:
x₁ = true(因为 belong[x₁] > belong[¬x₁])
x₂ = false(因为 belong[x₂] < belong[¬x₂])
验证:x₁ ∨ x₂ = true ∨ false = true ✓
先这样
接下来是网络流
先写一下费用流,以前没写过
#include<bits/stdc++.h>
using namespace std;
constexpr int maxn = 5010;
constexpr int maxm = 100010;
int n, m, S, t;
#define ll long long
ll maxflow, mincost;
int cnt = 1, now[maxn], head[maxn];
ll dis[maxn];
bool vis[maxn];
struct node{
int to, next;
ll val, cost;
}e[maxm];
void addedge(int u, int v, ll w, ll c){
e[++cnt].to = v;
e[cnt].val = w;
e[cnt].cost = c;
e[cnt].next = head[u];
head[u] = cnt;
cnt++;
e[cnt].to = u;
e[cnt].val = 0; // 反向边容量为0
e[cnt].cost = -c; // 反向边费用为负
e[cnt].next = head[v];
head[v] = cnt;
}
#define inf 0x3f3f3f3f3f3f3f3f
int spfa(){ // 找费用最短路,类似你原来的bfs
memset(dis, 0x3f, sizeof(dis));
memset(vis, 0, sizeof(vis));
memcpy(now, head, sizeof(now)); // 复制head到now,用于dfs
deque<int> q; // 使用双端队列优化SPFA
q.push_back(S);
dis[S] = 0;
vis[S] = 1;
while(!q.empty()){
int x = q.front();
q.pop_front();
vis[x] = 0;
for(int i = head[x]; i; i = e[i].next){
int y = e[i].to;
if(e[i].val > 0 && dis[y] > dis[x] + e[i].cost){
dis[y] = dis[x] + e[i].cost;
if(!vis[y]){
q.push_back(y);
vis[y] = 1;
}
}
}
}
return dis[t] != inf; // 能到达汇点就返回true
}
ll dfs(int x, ll sum){ // 和你的dfs几乎一样,沿最短路增广
if(x == t) return sum;
vis[x] = 1;
ll k, res = 0;
for(int i = now[x]; i && sum; i = e[i].next){
now[x] = i;
int y = e[i].to;
if(!vis[y] && e[i].val > 0 && dis[y] == dis[x] + e[i].cost){
k = dfs(y, min(sum, e[i].val));
if(k == 0) dis[y] = inf;
e[i].val -= k;
e[i ^ 1].val += k;
res += k;
sum -= k;
mincost += k * e[i].cost; // 关键:在这里累计费用
}
}
vis[x] = 0;
return res;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> S >> t;
int u, v;
ll w, c;
for(int i = 1; i <= m; i++){
cin >> u >> v >> w >> c;
addedge(u, v, w, c);
}
maxflow = 0;
mincost = 0;
while(spfa()){ // 找到最短路径
memset(vis, 0, sizeof(vis)); // 清空vis数组
maxflow += dfs(S, inf); // 沿最短路径增广
}
cout << maxflow << " " << mincost << endl;
return 0;
}
P3358 最长k可重区间集问题
费用流建模
考虑你最多给k的流量,原点容量为k,暴力显然是可以暴力,将线段拆为左端点和右端点,每条线段流量为1,然后从原点拉过来,然后向所有与他不相交的连流量为k的边。
但是你 \(n^2\) 会让你的SPFA爆炸,还有各种问题。
所以你离散化连边,只需要O(n)即可。
P4043 [AHOI2014/JSOI2014] 支线剧情
回溯操作很难搞,你没法在当前点数建模
所以就考虑边拆点,我们考虑一个边要能让他做什么,显然可以直接结束(如果是最大流的话,这个会保证),还可以往下走(废话),还可以跳到头。
但是回溯很难受,但是回溯 = 把当前贡献先给汇点,然后这条流就没了,等着树根接着往下流。
所以考虑u->v的边拆成两个点,i, i'

中间的inf流量0费用很好理解,i到T的也很好理解,贡献嘛,但是S到i‘的有点难理解,这么连的原因在与你贡献只是虚拟的,实际上流量还在,所以你贡献到T的还可以从S再接着往下。
P3980 [NOI2008] 志愿者招募
这是一个经典的
流量无用模型
你考虑时间轴,每段时间都需要ai的志愿者,那你就考虑时间轴上从左往右连接流量为inf-ai,费用为0的边,表示默认你这么多,因为最小费用最大流的前提是最大流,所以肯定流量你要达到inf,如何达到inf跑满呢,就需要志愿者边。
我们对于si,ti,连接一条si到ti+1,流量为inf,费用为c的边,代表s到t,每招募一个这个类型的志愿者(每流一个,要花费c)。
还有一个问题,你必须允许志愿者浪费,不然两个区间有交的话你没有办法重复贡献,导致出锅。
所以你要从T到S,每个点反着连不要钱且流量无限的边,这个因该很好理解。
做完了。
P2805 [NOI2009] 植物大战僵尸
先拓扑排序,把那种互相保护干不掉的,我们去掉。(注意!,一定要反图拓扑,否则会误判,也就是一个环里的点可能会保护其他的,但是你算不上,所以需要反图)
然后问题就变成了 最大权闭合子图
最大权闭合子图::实现
最大权闭合子图问题可以使用最小割解决OVO!。
连边方式
对于所有原图中的边 (u,v) ,连边 u→v ,容量为 INF 。
对于每个原图中的点 u ,设 u 的权值为 val[u] :
若 val[u]>0 (正权点),连边 S→u ,容量为 val[u] 。
若 val[u]<0 (负权点),连边 u→T ,容量为 −val[u] 。
至于 val[u]=0 (零权点)的情况,向 S 还是 T 连边对答案并没有影响(见下解释),所以可以不做特判。
如图所示,右边是原图,网络流连边如左图所示。
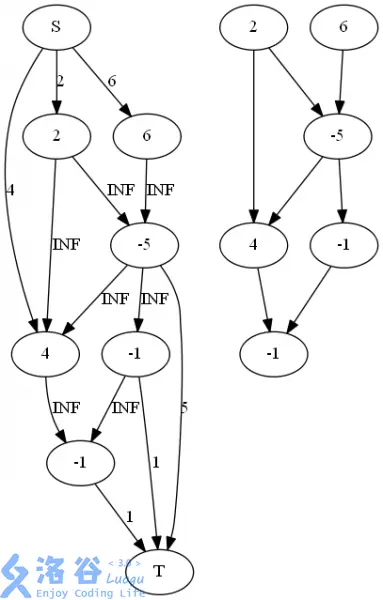
不用证明,感性理解,很对(bushi)
然后你就做完了。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号