后缀自动机 SAM

第几次学SAM了?

SAM

SAM 是一张有向无环图。结点被称作 状态，边被称作状态间的 转移。
图存在一个源点 \(t_0\)，称作 初始状态，其它各结点均可从 \(t_0\) 出发到达。
每个 转移 都标有某个字符。从一个结点出发的所有转移均 不同。
存在一个或多个 终止状态。如果我们从初始状态 \(t_0\) 出发，最终转移到了一个终止状态，则路径上的所有转移的标号连接起来一定是字符串 \(s\) 的一个后缀。反过来，\(s\) 的每个后缀均可用一条从 \(t_0\) 到某个终止状态的路径构成。
在所有满足上述条件的自动机中，SAM 的结点数是最少的。

直接对所有后缀建立AC自动机也满足这些性质，但是节点树是 \(n^2\)，SAM可以做到线性空间！

结束位置 endpos

\(\operatorname{endpos}(t)\) 为在字符串 \(s\) 中 \(t\) 的所有结束位置的集合（假设对字符串中字符的编号从零开始）。例如，对于字符串 \(\texttt{abcbc}\)，我们有 \(\operatorname{endpos}(\texttt{bc})=\{2,4\}\)。

后缀链接 link

\(v\) 的 后缀链接 \(\operatorname{link}(v)\) 连接到的状态，对应于 \(w\) 的后缀中与它的 \(\operatorname{endpos}\) 集合不同且最长的那个，也是 \(w\) 的后缀中在 \(s\) 中的出现次数比 \(w\) 更多且最长的那个。

太不直观了，上图！！！

以下是ababc的SAM，红色箭头是link，MAX是maxlen，size是当前节点endpos集合大小。

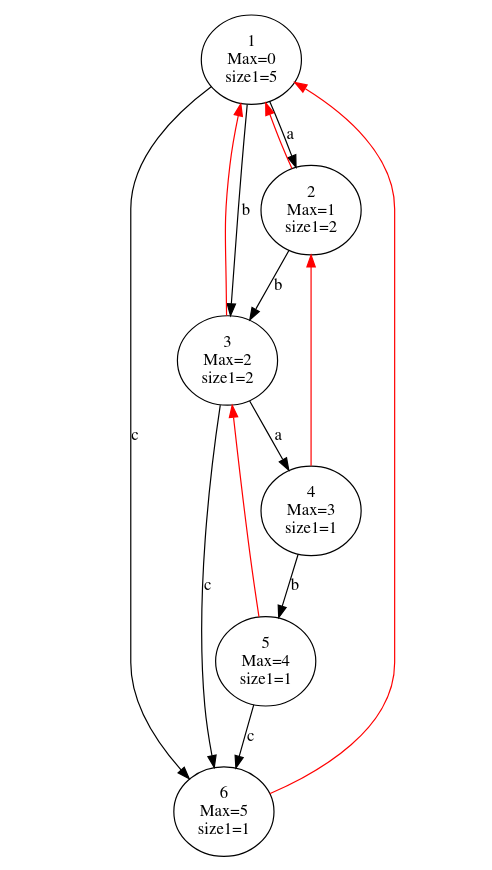
how to build?

struct SAM {
    int nxt[maxn][26], fa[maxn], len[maxn];
    int sz, las;
    ll cnt[maxn];
    int cnt_init[maxn];
    struct edge { int to, next; } e[maxn];
    int head[maxn], edgecnt;

    void addedge(int u, int v) {
        e[++edgecnt].to = v;
        e[edgecnt].next = head[u];
        head[u] = edgecnt;
    }

    void init() {
        sz = 1; las = 0;
        fa[0] = -1; len[0] = 0;
        memset(cnt_init, 0, sizeof cnt_init);
        memset(nxt[0], 0, sizeof nxt[0]);
        for (int i = 0; i < maxn; i++) cnt[i] = -1;
        edgecnt = 0;
    }

    void ext(int c) {
        int cur = sz++;
        len[cur] = len[las] + 1;
        cnt_init[cur] = 1;
        memset(nxt[cur], 0, sizeof nxt[cur]);

        int p = las;
        while (p != -1 && !nxt[p][c]) {
            nxt[p][c] = cur;
            p = fa[p];
        }
        if (p == -1) {
            fa[cur] = 0;
        } else {
            int q = nxt[p][c];
            if (len[q] == len[p] + 1) {
                fa[cur] = q;
            } else {
                int clone = sz++;
                len[clone] = len[p] + 1;
                memcpy(nxt[clone], nxt[q], sizeof nxt[q]);
                fa[clone] = fa[q];
                cnt_init[clone] = 0;
                while (p != -1 && nxt[p][c] == q) {
                    nxt[p][c] = clone;
                    p = fa[p];
                }
                fa[q] = fa[cur] = clone;
            }
        }
        las = cur;
    }

    void buildtree() {
        for (int i = 0; i < sz; i++) head[i] = -1;
        for (int i = 1; i < sz; i++) addedge(fa[i], i);
    }

    ll dfs(int u) {
        if (cnt[u] != -1) return cnt[u];
        ll res = cnt_init[u];
        for (int i = head[u]; i != -1; i = e[i].next) {
            res += dfs(e[i].to);
        }
        return cnt[u] = res;
    }
} sam;

我们先要把自动机建出来，这一部分是函数ext，构建是在线的。

例子，一看就懂，记得时刻想SAM的性质：

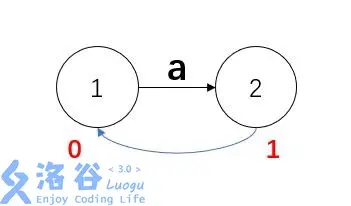
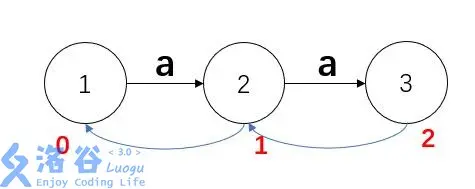
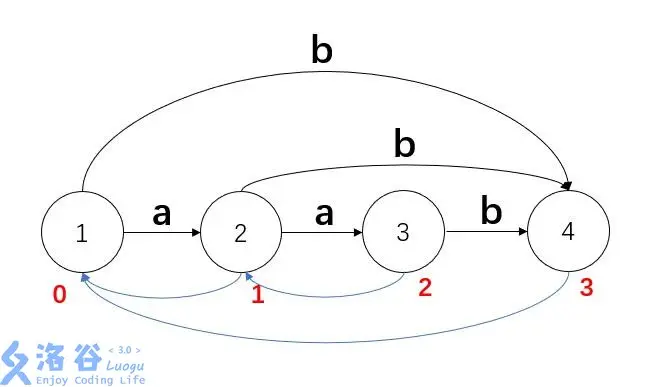
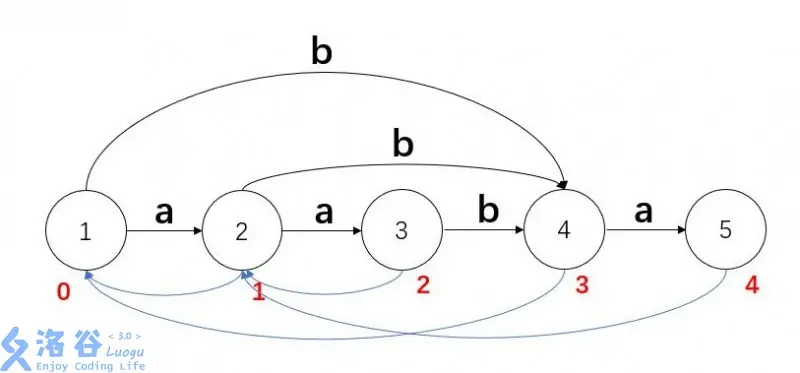
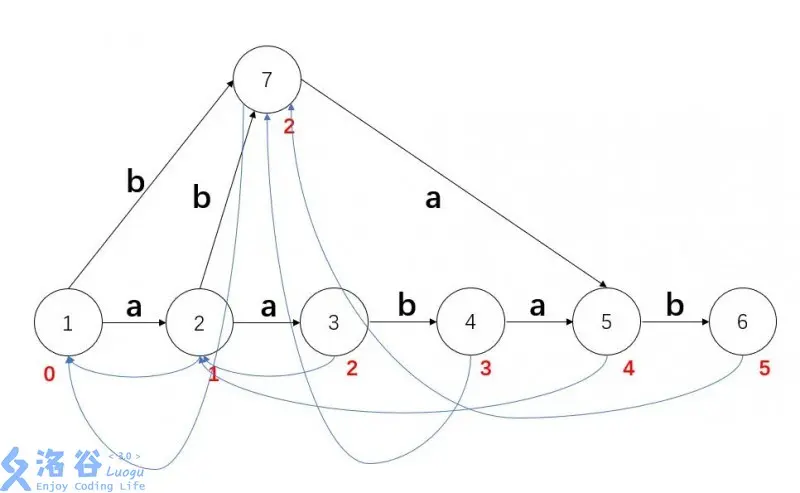
这里clone的原因是因为如果直接加的话ab和aab都到达4，但二者endpos不同。

然后你可以记忆化搜索出来cnt。

应用

检查字符串是否出现

直接跑一遍即可。

不同子串个数

即为 SDOI2016 生成魔咒

即每个节点对应的子串数量是 \(\operatorname{len}(v)-\operatorname{len}(\operatorname{link}(v))\)，对自动机所有节点求和即可。

所有不同子串的总长度

减去其 \(\operatorname{link}\) 节点的对应值就是该节点的净贡献，对自动机所有节点求和即可。

字典序第 k 大子串

即P3975 [TJOI2015] 弦论

若本质不同，一个节点后的所有子串大小即为size
否则记忆化搜索出来转移边树大小即可。

最小循环移位

所以问题简化为在 \(S+S\) 对应的后缀自动机上寻找最小的长度为 \(|S|\) 的路径，这可以通过平凡的方法做到：我们从初始状态开始，贪心地访问最小的字符即可。

出现次数

对于一个给定的文本串 \(T\)，有多组询问，每组询问给一个模式串 \(P\)，回答模式串 \(P\) 在字符串 \(T\) 中作为子串出现了多少次。

利用后缀链接树的信息，进行 dfs 即可预处理每个节点的 \(\operatorname{endpos}\) 集合的大小。

所有「前缀节点」的初始集合大小为 \(1\)，非「前缀节点」的初始集合大小为 \(0\)。然后，沿着后缀链接自下向上回溯时，每个父节点的集合大小都加上它的所有子节点的集合大小（不要遗漏父节点本身的初始值）。这样得到的每个节点处的值，就是该节点的 \(\operatorname{endpos}\) 集合的大小。不同子节点的集合大小可以直接相加的理由是，同一个 \(v_i\) 只会出现在一个子树内，故而相加不会重复。

\(B=\sum_{1≤i<j≤n} \lcp(T_i,T_j)\)

即P4248 [AHOI2013] 差异

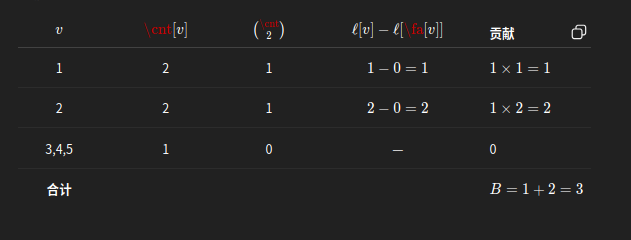
利用 SAM 对所有后缀公共前缀的性质，将"\(\lcp\)"问题还原为状态路径长度的统计。

状态 \(v\) 表示一批极大同等后缀的公共区间，它们对每对组合都贡献了同样的 \(\ell[v]-\ell[\fa[v]]\)；对这一区间内的每一步都恰好被那 \(\cnt[v]\) 个后缀共享。

没有漏算也无重算，因为 SAM 各状态切分了不同的"新"子串长度区间，且父链接保证区间不重叠且连贯。

字符串中恰好出现了 k 次的子串，子串长度出现次数最多的长度数

即一个siz(cnt) = k的节点所有表示的子串是可行的，长度一定是连续区间(lenfai,leni]，差分即可。

s 中有多少个连续子串与 x_i 是循环同构的

即 CF235C Cyclical Quest

先用kmp求出来最小循环节。
然后我们在 SAM 上从状态 p 尝试通过字符 c 进行转移。

如果 sam.nxt[p][c] 存在，我们就转移过去：p = sam.nxt[p][c]，l++。

如果不存在，说明以当前匹配的子串为后缀，无法接上字符 c。我们需要缩短当前匹配的子串，即沿着后缀链接向上跳：p = sam.fa[p]，同时更新匹配长度 l = sam.len[p]。持续这个过程，直到找到一个可以匹配 c 的状态，或者回到根节点。

if (l >= n):
如果成立，说明我们在 s 中找到了一个长度至少为 n 的子串，它同时也是 t 的子串，因此是 x 的一个循环同构串。

当前状态 p 的 maxlen 可能大于 n。我们需要找到代表这个长度为 n 的循环同构串的最本质的状态。这个状态是 p 或 p 的祖先中，maxlen 大于等于 n 且 fa 节点的 maxlen 小于 n 的那一个。我们可以通过循环 while (sam.len[sam.fa[p]] >= n) 不断令 p = sam.fa[p] 来找到它。

为了防止对同一个状态重复计数，我们引入一个时间戳 ts。每个查询 ts 加一。如果当前找到的状态 p 的标记 mark[p] != ts，我们就将 sam.cnt[p] 加入答案，并更新 mark[p] = ts。