20250610 GYX 树上DP

GYX 树形

太简单/板子就没有放

[NOIP 2018 提高组] 赛道修建

显然要二分。
考虑如何check。
一个自树肯定是自己选一条然后如果又机会的话还能贡献一条最大的给上面。
我们考虑二分这个大于mid的第一条链，然后加入答案，将次大的贡献给父亲。
为什么是最优的？考虑反正法。
如果你当前不选正好满足大于mid的最小的而是选择更大的，那么如果父亲恰好需要你这个更大的，那就炸了。

然后二分+树上合并即可。

用DFS的方式，从下往上把树不停的“消层”，直至没有。

需要注意的是，最下层解决完毕以后，后面的层的链是边权+点权，这才是我们的链。当然也可以看作最下层的点权是0。

在全局的设个变量res记录还需要找到几条赛道。

---

CF1039D

有一棵 n 个节点的树。

其中一个简单路径的集合被称为 k 合法当且仅当：

树的每个节点至多属于其中一条路径，且每条路径恰好包含 k 个点。

对于 k∈[1,n]，求出 k 合法路径集合的最多路径数 即：设 k 合法路径集合为 S，求最大的 ∣S∣。

我们发现可以根号分治。
因为
你k大于根号n的话答案一定小于根号n

这一部分我们直接枚举链的条数，答案是不升的，所以只需要二分每个ans的k即可，因为一共最多根号n次二分，每次check是O(n)的。

k<=n的话和上一题差不多。
只不过需要维护最小值和次小值，因为可能是两个儿子+lca

记 mx1​,mx2​ 为 i 的儿子所传入的最长的两条链（所经过点的个数），若 mx1​+mx2​+1≥k，那么显然是将 i 与它的两个儿子配成一条链，答案加 1；否则将 mx1​+1 传上去到 fai​ 即可。这样一次 DP 就是 O(n) 的。

---

CF1485E Move and Swap

有一棵树，以1为根，叶子结点深度相同,结点 i 有权值 ai​。现在有红蓝两颗棋子，每一步可以进行如下操作：

把红色棋子移动到它的子节点
把蓝色棋子移动到它下一层的任何一个结点
选择交换或不交换红子与蓝子的位置
计算得分为 ∣ared​−ablue​∣

问最大的得分和

---

显然两个点一定在一层且蓝点爱去哪去哪，所以状态f x y 蓝x红y就变成了只需要记录f u表示红点在u时候的答案。

向下转移，如何不交换
蓝点肯定在最大值/最小值。

f[u] = f[fa[u]] + MAX{d[u]} - a[u]
f[u] = f[fa[u]] + a[u] - MIN{d[u]}

然后如果是交换，蓝点在v的话

f[v] = f[fa[u]] + |au - av|

因为绝对值很难处理并且无法最优化，所以|au - av| -> max(au - av,av - au)

答案就变成了 f[v] = f[fa[u]] + max(au - av,av - au)

我们肯定不能这样转移，并且注意到v是不会变的，所以拆开。

f[v] = max(au + f[fa[u]]) - av;
f[b] = max(-au + f[fa[u]]) + av;

这样只需要维护一下这一层的 max(au + f[fa[u]]) 和 max(au + f[fa[u]]) 即可。

---

[SHOI 2014] 概率充电器

SHOI 概率充电器由 n−1 条导线连通了 n 个充电元件。进行充电时，每条导线是否可以导电以概率决定，每一个充电元件自身是否直接进行充电也由概率决定。随后电能可以从直接充电的元件经过通电的导线使得其他充电元件进行间接充电。

求进入充电状态的元件个数的期望是多少。

换根DP

每一个节点通电，可能是：自己有电，子树来电，非子树来电。

我们设h[x]表示节点x通电的概率，先统计只有子树会来电。

通电一定是 自己来电 或者 儿子来电。

一个事件A和B至少发生一个的概率为P(a) + P(b) - P(a) * P(b) 不需要解释。

a事件的概率就是自己来电，b事件的概率就是儿子来电，也就是val(x,y) * v[y]，这个贡献是可以加的。

注意，目前h[i] = 节点 i 本身来电 的概率 q[i] +来自每个子节点 j 的供电概率 h[j] * p(i,j)

然后我们考虑这样dp之后从非子树来的怎么统计。

我们用其他点传到父亲的概率来更新这个儿子。

那么一个儿子j有电并且能传到本节点的概率B加上除了儿子来电的概率A再减去乘积就是h[i]

就可以算出来P(A)，注意，P(a)是自己和其他子树的来电概率

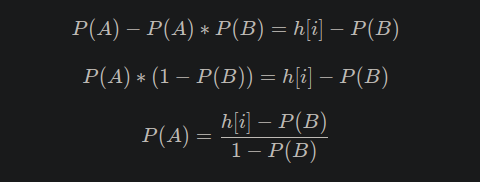
我们要把这个P(A)传给儿子j

自然是h[j]=h[j]+(P(A)∗p(i,j))−h[j]∗P(A)∗p(i,j)

注意小心除以0。