矩阵快速幂 学习笔记。
https://www.luogu.com/article/gh3khavx
巨佬wjy的博客
矩阵乘法定义
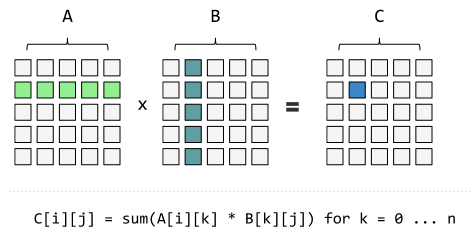
一些约定:
⊗ 有交换律:a⊗b=b⊗a;
⊗ 有结合律:(a⊗b)⊗c=a⊗(b⊗c);
⊗ 对 ⊕ 有分配律:a⊗(b⊕c)=(a⊗b)⊕(a⊗c);
广义矩阵乘法:
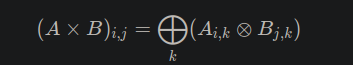
struct Matrix{
int mat[MN][MN];
Matrix(int x=0){
memset(mat,0,sizeof(mat));
if(!x) return;
for(int i=0;i<MN;i++) mat[i][i]=x;
}
Matrix operator*(const Matrix x)const{
Matrix ret;
for(int i=0;i<MN;i++){
for(int j=0;j<MN;j++){
for(int k=0;k<MN;k++){
ret.mat[i][j]+=mat[i][k]*x.mat[k][j];
}
}
}
return ret;
}
};
---
# USACO07NOV Cow Relays G——Floyd倍增转移
给定一张 T 条边的无向连通图,求从 S 到 E 经过 N 条边的最短路长度。
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
这是弗洛伊德,这其实是一个广义的矩阵乘法。
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
C[i][j]=min(C[i][j],A[i][k]+A[k][j]);
}
Ax是表示A经过了x条边的最短路。
就解决了。
```cpp
#include <bits/stdc++.h>
using namespace std;
constexpr int maxn = 510;
int n, s, t, e, tot;
struct Matrix {
int mt[maxn][maxn];
Matrix operator *(const Matrix &x) const {
Matrix ans;
memset(ans.mt, 0x3f, sizeof ans.mt);
for (int k = 1; k <= tot; k++) {
for (int i = 1; i <= tot; i++) {
for (int j = 1; j <= tot; j++) {
ans.mt[i][j] = min(ans.mt[i][j], mt[i][k] + x.mt[k][j]);
}
}
}
return ans;
}
};
Matrix dis, ans;
unordered_map<int, int> ump;
Matrix qpow() {
n--;
ans = dis;
while (n) {
if (n & 1) {
ans = ans * dis;
}
dis = dis * dis;
n >>= 1;
}
return ans;
}
int main() {
cin >> n >> t >> s >> e;
memset(dis.mt, 0x3f, sizeof dis.mt);
for (int i = 1; i <= t; i++) {
int w, u, v;
cin >> w >> u >> v;
if (!ump[u]) ump[u] = ++tot;
if (!ump[v]) ump[v] = ++tot;
int uid = ump[u], vid = ump[v];
dis.mt[uid][vid] = dis.mt[vid][uid] = w;
}
cout << qpow().mt[ump[s]][ump[e]] << endl;
return 0;
}ell
SCOI2009迷路——边权拆点
给定一个 n 个点,m 条边的有向图,边权为 w,求从 1 号点出发长度为 k 到达 n 号点的路径方案数(n≤10,w≤9,k≤109)。
有一个套路---边权拆点,注意到边权很小,所以可以拆成边权都是1的链!
ft[i][j]=k⟺ i到j的长度为t的路径条数为k。
显然有 ft[i][j]=k=1∑nft−1[i][k]×f1[k][j]。
然后矩阵快速幂即可!
#include<bits/stdc++.h>
using namespace std;
constexpr int N=128;
constexpr int mod = 2009;
int n,T;
struct Matrix{
int a[N][N];
void clear(){
memset(a,0,sizeof(a));
}
}a;
Matrix operator *(Matrix a,Matrix b){
Matrix res;
res.clear();
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
for(int k = 1;k <= n;k++){
res.a[i][j] = (res.a[i][j] + a.a[i][k] * b.a[k][j] % mod) % mod;
}
}
}
return res;
}
Matrix operator ^(Matrix a,int b){
Matrix re;re.clear();
for(int i=1;i<=n;i++)re.a[i][i]=1;
while(b){
if(b&1)re=re*a;
a=a*a;
b>>=1;
}
return re;
}
int main(){
//ios::sync_with_stdio(0);
cin>>n>>T;
int n1=n;
n=n*9;
for(int i=1;i<=n1;i++){
for(int j=1;j<=8;j++){
a.a[9*(i-1)+j][9*(i-1)+j+1]=1;
}
}
char s[32];
for(int i=1;i<=n1;i++){
scanf("%s",s+1);
for(int j=1;j<=n1;j++){
if(s[j]>'0'){
a.a[9*(i-1)+s[j]-'0'][9*(j-1)+1]=1;
}
}
}
a=a^T;
printf("%d",a.a[1][n1*9-8]);
return 0;
}
HH去散步
给定 n 个点,m 条无向边的图,边权均为 1,求从 S→T 的路径上有多少长度为 t 的路径,满足上一步走过的路下一步不能重复走。答案对 45989 取模。 1≤n≤50,1≤m≤60,t≤230,0≤S,T。
发现问题再与 满足上一步走过的路下一步不能重复走。
我们可以构造一些额外点,然后把边定向,来满足这些约束。
具体构造方法在脑子里。
设 f(i,j) 表示走到第 i 个点,路径长度为 j 的路径条数,显然有转移方程
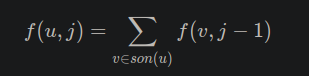
然后矩阵快速幂即可
#include <bits/stdc++.h>
using namespace std;
const int mod = 45989;
struct Mat {
int m[150][150], r, c;
Mat() { memset(m, 0, sizeof(m)); }
Mat operator*(const Mat &a) const {
Mat t;
t.r = r; t.c = a.c;
for (int i = 1; i <= r; i++)
for (int j = 1; j <= t.c; j++)
for (int k = 1; k <= c; k++)
t.m[i][j] = (t.m[i][j] + (m[i][k] * a.m[k][j]) % mod) % mod;
return t;
}
} a, b;
struct Edge { int u, v; } e[127];
int head[57], nxt[127], cnt;
int n, m, s, t, x;
Mat operator^(Mat a, int k) {
Mat res;
res.r = a.r; res.c = a.c;
for (int i = 1; i <= a.r; i++) res.m[i][i] = 1;
while (k) {
if (k & 1) res = res * a;
a = a * a;
k >>= 1;
}
return res;
}
int rev(int x) { return x % 2 == 0 ? x - 1 : x + 1; }
int main() {
ios::sync_with_stdio(0);
cin >> n >> m >> x >> s >> t;
if (x == 0) {
cout << 0;
return 0;
}
s++; t++;
for (int i = 1, u, v; i <= m; i++) {
cin >> u >> v; u++; v++;
e[++cnt] = {u, v}; nxt[cnt] = head[u]; head[u] = cnt;
e[++cnt] = {v, u}; nxt[cnt] = head[v]; head[v] = cnt;
}
for (int i = 1; i <= cnt; i++)
for (int k = head[e[i].v]; k; k = nxt[k])
if (k != rev(i)) b.m[k][i]++;
b.r = b.c = cnt;
a.r = cnt; a.c = 1;
for (int i = head[s]; i; i = nxt[i]) a.m[i][1]++;
b = b ^ (x - 1);
b = b * a;
int ans = 0;
for (int i = head[t]; i; i = nxt[i])
ans = (ans + b.m[rev(i)][1]) % mod;
cout << ans;
return 0;
}
HAOI2015 数字串拆分
NOI2013 矩阵游戏
婷婷是个喜欢矩阵的小朋友,有一天她想用电脑生成一个巨大的 n 行 m 列的矩阵(你不用担心她如何存储)。她生成的这个矩阵满足一个神奇的性质:若用 F[i,j] 来表示矩阵中第 i 行第 j 列的元素,则 F[i,j] 满足下面的递推式:
F[1,1]F[i,j]F[i,1]=1=a×F[i,j−1]+b,=c×F[i−1,m]+d,j=1i=1
递推式中 a,b,c,d 都是给定的常数。
现在婷婷想知道 F[n,m] 的值是多少,请你帮助她。由于最终结果可能很大,你只需要输出 F[n,m] 除以 109+7 的余数。
000
转移矩阵显然可以是A1
a b
0 1
A2
c d
0 1
然后答案就是 A1m−1(A2A1m−1)n−1A3
然后矩阵快速幂用十进制快速幂可以冲过去,但是显然有更不优雅的做法。
注意到这个矩阵对于列的转移,其中 a 总共被乘上了 am−1 次,同理与 cn−1,而注意到模数为质数,可以考虑费马小定理取模,模上 φ(MOD) 即可。
注意到,当 a=c=1 时不能用费马小定理,考虑直接矩阵快速幂的幂取模原来模数。
#include <bits/stdc++.h>
#define int __int128
using namespace std;
constexpr int MN = 15, MOD = 1e9 + 7;
int n, m, a, b, c, d, base0, base1;
string sn, sm;
struct Matrix {
int mat[MN][MN];
Matrix(int x = 0) {
memset(mat, 0, sizeof(mat));
for (int i = 0; i < MN; i++) mat[i][i] = x;
}
Matrix operator*(const Matrix &x) const {
Matrix ret;
for (int i = 0; i < MN; i++) {
for (int j = 0; j < MN; j++) {
for (int k = 0; k < MN; k++) {
ret.mat[i][j] += mat[i][k] * x.mat[k][j];
ret.mat[i][j] %= MOD;
}
}
}
return ret;
}
} M1, M2;
Matrix qpow(Matrix A, int B) {
Matrix ret(1);
while (B > 0) {
if (B & 1) ret = ret * A;
A = A * A;
B >>= 1;
}
return ret;
}
void read128(int &x, string &s) {
cin >> s;
x = 0;
for (char ch : s) {
x = (x * 10 + (ch - '0'));
}
}
void readInt(int &x) {
long long tmp;
cin >> tmp;
x = tmp;
}
void print128(int x) {
if (x == 0) {
cout << "0\n";
return;
}
string res;
while (x) {
res += char(x % 10 + '0');
x /= 10;
}
reverse(res.begin(), res.end());
cout << res << "\n";
}
signed main() {
cin >> sn >> sm;
readInt(a), readInt(b), readInt(c), readInt(d);
base0 = (a == 1 ? MOD : MOD - 1);
for (auto p : sm) {
m = ((m * 10) + (p - '0')) % base0;
}
Matrix ans;
M1.mat[0][0] = a, M1.mat[0][1] = b, M1.mat[1][1] = 1;
M2.mat[0][0] = c, M2.mat[0][1] = d, M2.mat[1][1] = 1;
ans.mat[0][0] = ans.mat[1][0] = 1;
Matrix d = qpow(M1, (m + base0 - 1) % base0) * M2;
if (d.mat[0][0] == 1) base1 = MOD;
else base1 = MOD - 1;
for (auto p : sn) {
n = ((n * 10) + (p - '0')) % base1;
}
ans = qpow(d, (n + base1 - 1) % base1) * qpow(M1, (m + base0 - 1) % base0) * ans;
print128(ans.mat[0][0]);
return 0;
}






 浙公网安备 33010602011771号
浙公网安备 33010602011771号