xyh数据结构
[Ynoi2012] NOIP2015 充满了希望
给一个长为 n 的序列,有 m 个操作,操作编号从 1 到 m,每个操作为:
1 x y:将序列位置为 x,y 的两个元素交换。
2 l r x:将序列区间 [l,r] 内所有元素修改为 x。
3 x:查询序列 x 位置的值。
现在有 q 次查询,每次查询给出一个操作的区间 [l,r]:
先将序列中的元素全部置为 0,之后依次进行从 l 到 r 的所有操作,求出所有这些操作中所有 3 操作的答案的和。
显然
一次操作的贡献在于他最左侧第一个出现的区间覆盖操作,我们建立一颗线段树来维护这个东西。建立线段树,对于操作1区间交换,操作2区间修改,操作3把pre query出来。
这样我们可以得到一个pre数组表示第i个操作3是由于哪一次区间覆盖产生的贡献。
然后我们进行扫描线,这个扫描线比较特殊,我们将l从大到小排序,对于那些询问点中pre再左端点后面的在树桩树组上单点修改,区间直接区间查询即可,使用树桩数组维护。
有错别字间两。
#include<bits/stdc++.h>
using namespace std;
#define ls(p) p*2
#define rs(p) p*2+1
#define ll long long
#define se second
#define fi first
const int maxn=1e6+5;
namespace Seg{
struct node{
int lazy,num,l,r;
}tr[maxn*4];
inline void push_down(int p){
if(tr[p].l==tr[p].r&&tr[p].lazy!=-1) tr[p].num=tr[p].lazy,tr[p].lazy=-1;
else if(tr[p].lazy!=-1)
{
tr[ls(p)].lazy=tr[ls(p)].num=tr[p].lazy;
tr[rs(p)].lazy=tr[rs(p)].num=tr[p].lazy;
tr[p].lazy=-1;
}
}
inline void build(int p,int l,int r){
tr[p].l=l,tr[p].r=r;
tr[p].lazy=-1;
if(l==r) return ;
int mid=(l+r)>>1;
build(ls(p),l,mid),build(rs(p),mid+1,r);
}
inline void change(int p,int l,int r,int lx,int rx,int num){
if(l>rx||r<lx) return ;
push_down(p);
if(lx<=l&&r<=rx){tr[p].lazy=num;return ;}
int mid=(l+r)>>1;
change(ls(p),l,mid,lx,rx,num);change(rs(p),mid+1,r,lx,rx,num);
}
inline int qry(int p,int l,int r,int pos){
push_down(p);
if(l==r) return tr[p].num;
int mid=(l+r)>>1;
if(pos<=mid) return qry(ls(p),l,mid,pos);
else return qry(rs(p),mid+1,r,pos);
}
}
struct BIT{
#define N 1e6
ll ts[maxn];
inline int lowbit(int x){return x&(-x);}
inline void updata(int x,int y){for(;x<=N;x+=lowbit(x)) ts[x]+=y;}
inline ll query(int x){ll sum=0;for(;x;x-=lowbit(x)) sum+=ts[x];return sum;}
}T;
int n,m,q;
int pre[maxn],val[maxn];
ll ans[maxn];
struct node{int l,r,id;}qr[maxn];
priority_queue< pair<int,pair<int,int>> >que;
inline bool cmp(node a,node b){return a.l>b.l;}
signed main(){
ios::sync_with_stdio(0);
cin>>n>>m>>q;
Seg::build(1,1,n);
for(int i=1;i<=m;i++){
int op,l,r,x;
cin>>op;
if(op==1){
cin>>l>>r;
int pl=Seg::qry(1,1,n,l),pr=Seg::qry(1,1,n,r);
Seg::change(1,1,n,l,l,pr);
Seg::change(1,1,n,r,r,pl);
}
else if(op==2){
cin>>l>>r>>x;
Seg::change(1,1,n,l,r,i);
val[i]=x;
}
else{
cin>>x;
pre[i]=Seg::qry(1,1,n,x);
val[i]=val[pre[i]];
que.push({pre[i],{i,val[i]}});
}
}
for(int i=1;i<=q;i++){
int l,r;
cin>>l>>r;
qr[i].l=l,qr[i].r=r;
qr[i].id=i;
}
sort(qr+1,qr+q+1,cmp);
for(int i=1;i<=q;i++){
while(!que.empty()){
if(que.top().fi>=qr[i].l) T.updata(que.top().se.fi,que.top().se.se),que.pop();
else break;
}
ans[qr[i].id]=T.query(qr[i].r)-T.query(qr[i].l-1);
}
#define endl '\n'
for(int i=1;i<=q;i++) cout<<ans[i]<<endl;
}
[SDOI2015] 寻宝游戏
小 B 最近正在玩一个寻宝游戏,这个游戏的地图中有 N 个村庄和 N−1 条道路,并且任何两个村庄之间有且仅有一条路径可达。游戏开始时,玩家可以任意选择一个村庄,瞬间转移到这个村庄,然后可以任意在地图的道路上行走,若走到某个村庄中有宝物,则视为找到该村庄内的宝物,直到找到所有宝物并返回到最初转移到的村庄为止。
小 B 希望评测一下这个游戏的难度,因此他需要知道玩家找到所有宝物需要行走的最短路程。但是这个游戏中宝物经常变化,有时某个村庄中会突然出现宝物,有时某个村庄内的宝物会突然消失,因此小 B 需要不断地更新数据,但是小 B 太懒了,不愿意自己计算,因此他向你求助。为了简化问题,我们认为最开始时所有村庄内均没有宝物。
询问转化为
给一些动态的点,求包含这些点的最小树的辩权和。
一开始望淀粉树去想了
考虑拍到dfs序上,然后我们发现所有点按dfs序排序后这个最小树边权和就等于1/2*dist(a1,a2) + 1/2(dist(a2,a3))....1/2 dist(an,a1),可以画图理解。
然后我们就直接使用set或者平衡树来维护这个点集,插入点就找到点x两侧的y,z,然后添加disxy disxz再删去disyz,删除同理。
然后就做完了,细节非常多。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int MAXN = 100000 + 5;
struct Edge {
int to, nxt, w;
} e[MAXN * 2];
int head[MAXN], ecnt;
void add_edge(int u, int v, int w) {
e[++ecnt] = {v, head[u], w};
head[u] = ecnt;
}
int N, M;
int dfn[MAXN], idfn[MAXN], dfc;
int dep[MAXN], son[MAXN], siz[MAXN], top[MAXN], fa[MAXN];
ll depth_w[MAXN];
void dfs1(int u, int p) {
fa[u] = p;
siz[u] = 1;
dep[u] = dep[p] + 1;
dfn[u] = ++dfc;
idfn[dfc] = u;
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (v == p) continue;
depth_w[v] = depth_w[u] + e[i].w;
dfs1(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int tp) {
top[u] = tp;
if (son[u]) dfs2(son[u], tp);
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
int lca(int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) swap(x, y);
x = fa[top[x]];
}
return dep[x] < dep[y] ? x : y;
}
ll dist(int x, int y) {
int z = lca(x, y);
return depth_w[x] + depth_w[y] - 2 * depth_w[z];
}
bool vis[MAXN];
set<int> st;
ll ans = 0;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> N >> M;
for (int i = 1; i < N; i++) {
int u, v, w;
cin >> u >> v >> w;
add_edge(u, v, w);
add_edge(v, u, w);
}
dfs1(1, 0);
dfs2(1, 1);
while (M--) {
int u;
cin >> u;
int x = dfn[u];
if (!vis[u]) {
st.insert(x);
auto it_lo = st.lower_bound(x);
int y_dfn = (it_lo == st.begin()
? *prev(st.end())
: *prev(it_lo));
auto it_hi = st.upper_bound(x);
int z_dfn = (it_hi == st.end()
? *st.begin()
: *it_hi);
int y = idfn[y_dfn];
int z = idfn[z_dfn];
ll d = dist(u, y) + dist(u, z) - dist(y, z);
ans += d;
vis[u] = true;
}
else {
auto it_lo = st.lower_bound(x);
int y_dfn = (it_lo == st.begin()
? *prev(st.end())
: *prev(it_lo));
auto it_hi = st.upper_bound(x);
int z_dfn = (it_hi == st.end()
? *st.begin()
: *it_hi);
int y = idfn[y_dfn];
int z = idfn[z_dfn];
ll d = dist(u, y) + dist(u, z) - dist(y, z);
ans -= d;
st.erase(x);
vis[u] = false;
}
cout << ans << "\n";
}
return 0;
}
归程 这里不写、
[THUPC 2017] 天天爱射击
小 C 爱上了一款名字叫做《天天爱射击》的游戏。如图所示,这个游戏有一些平行于 x 轴的木板。现在有一些子弹,按顺序沿着 y 轴方向向这些木板射去。第 i 块木板被 Si 个子弹贯穿以后,就会碎掉消失。一个子弹可以贯穿其弹道上的全部木板,特别的,如果一个子弹触碰到木板的边缘,也视为贯穿木板。
小 C 现在知道了游戏中 n 块木板位置,以及知道了 m 个子弹射击位置。现在问你每个子弹射出去以后,有多少木板会碎掉?
贴一张图
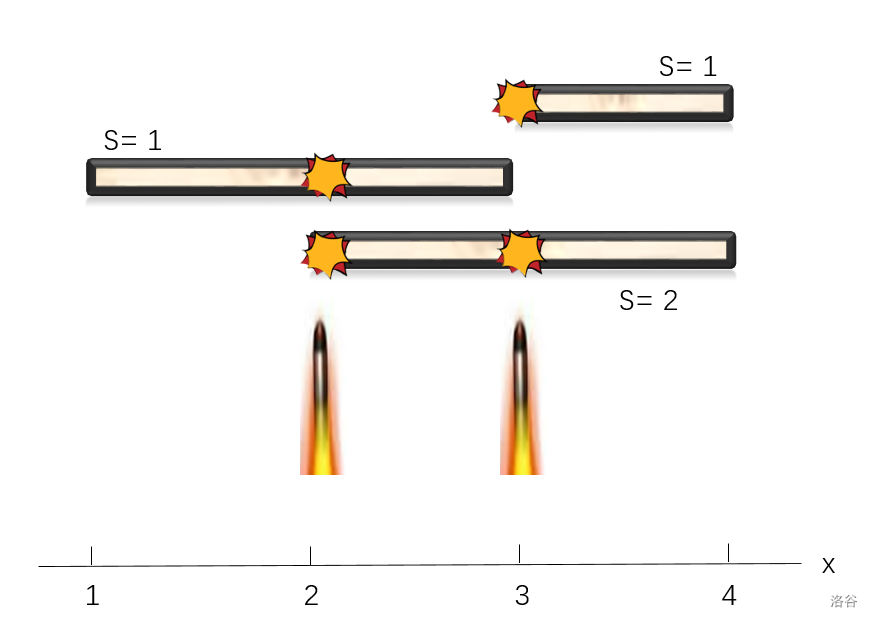
整体二分
然后
将子弹排序整体二分,一开始是(l,r)(1, m+1) (m+1是因为有可能会有无法击碎的木板)
对于一个木板,我们进行二分,将能击碎这个木板的点分为一类,不能的分为一类,递归下去二分
如果l == r 那就统计答案。
对于一个木板被l ,r 区间的子弹打中的次数,直接使用树状数组维护。
A Simple Task
This task is very simple. Given a string S of length n and q queries each query is on the format i j k which means sort the substring consisting of the characters from i to j in non-decreasing order if k = 1 or in non-increasing order if k = 0.
Output the final string after applying the queries.
26个字母,桶排是O(n)的,显然太慢,似乎无法优化?
发现瓶颈在于选取和修改,所以可以用线段树优化。
开一颗线段树,节点维护26个字母的数量,对于一个区间的排序,先query一次,然后再区间修改26次,就可以26*logn排序了。
B - 采花
类似HH的项链,但是颜色只有出现超过2次才会被统计。
HH的项链维护last[i]表示上一次出现,这里直接维护lst1和lst2表示上一次和上上次出现的位置,然后扫描线即可。
#include<bits/stdc++.h>
using namespace std;
constexpr int maxn = 2e6+10;
struct node{
int l,r,pos;
}t[maxn];
int last1[maxn],last2[maxn];
int a[maxn];
int n, m, q;
inline int lowbit(int x){return x & -x;}
int tree[maxn << 2];
void add(int x,int v){
for(int i = x;i <= n;i += lowbit(i)) tree[i] += v;
}
int query(int x){
int res = 0;
for(int i = x;i;i -= lowbit(i)) res += tree[i];
return res;
}
int ans[maxn];
int main(){
cin>>n>>q>>m;
for(int i = 1;i <= n;i++){
cin>>a[i];
}
for(int i = 1;i <= m;i++){
cin>>t[i].l>>t[i].r;
t[i].pos = i;
}
sort(t+1,t+1+m,[](node x,node y){
return x.r < y.r;
});
int j = 1;
for(int i = 1;i <= m;i++){
for(;j <= t[i].r;j++){
if(!last1[a[j]]) last1[a[j]] = j;
else{
if(!last2[a[j]]){
add(last1[a[j]],1);
last2[a[j]] = j;
}
else{
add(last2[a[j]],1);
add(last1[a[j]],-1);
last1[a[j]] = last2[a[j]];
last2[a[j]] = j;
}
}
}
ans[t[i].pos] = query(t[i].r) - query(t[i].l-1);
}
for(int i = 1;i <= m;i++) cout<<ans[i]<<'\n';
return 0;
}






 浙公网安备 33010602011771号
浙公网安备 33010602011771号