2025/4/24 省队集训(不是省队) Day1-Day7
模拟赛
P1014. 机器人大师(bot

输入数据 1
3 3 0
1 11
3 8
5 15
10 13
12 18
16 20
输出数据 1
6
首先先将问题进行转化。
显然,只有机器人才会产生时间消耗。
我们将区间列出来,我们将区间的两个端点统称为“端点”,一个机器人区间的贡献即为此区间左端点到这个端点的下一个端点的时间加上此区间右端点到前一端点时间。且每个端点与端点之间的”块“只会被计算一次。
然后考虑建立二分图,二分图左部点为区间,右部点为左右两个端点之间的”块“
一个区间显然会向右部点两个块连边,表示两个块会对这个区间产生贡献。
然后我们将块视为点,区间视为边。
块长视为点权,区间编号视为边的编号,显然可以从二分图抽出来若干条链
然后用点权为INF的点将这些链链接为一条。
问题就转化为了:
一条链,要选m条边,求最小的点权和(选一条边就要选与其相邻的两个点)
DP+滚动数组即可。
环形分割
题目描述
给定一个长度为nn的字符串环SS,第一个字符与最后一个字符相连,要求将SS分成恰好kk个非空子串,求其中字典序最大的子串的最小可能字典序。
输入格式
第一行两个整数n,kn,k 第二行一个字符串SS
输出格式
一行一个字符串表示答案
样例输入1
20 3
bbbaaaaabbabaabbbbaa
样例输出1
aaabbabaabbbbaabbb
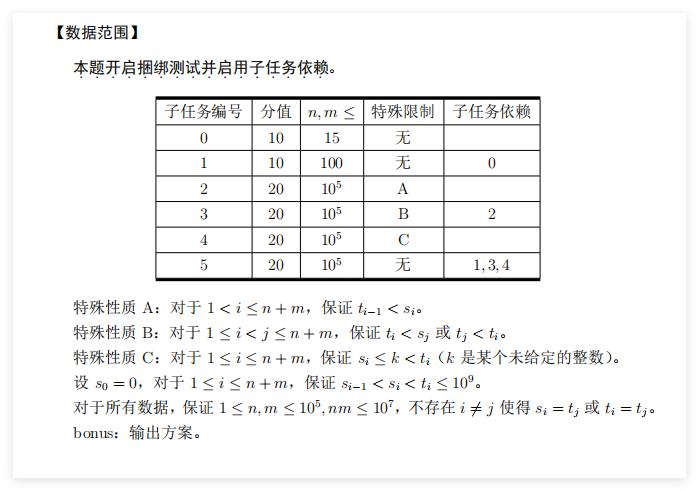
数据范围
子任务编号 分值 n≤n≤
1 20 50
2 10 80
3 100
4 200
5 700
6 20 3000
7 100000
逆天题,N个算法堆一块
观察发现整个环状串切成一个字典序最小的串时那个分割点一定会成为分割为k个串的分割点之一。
我们二分的答案显然是要求分割出来的k个串字典序都小于等于答案。
很不好求。
我们考虑求两个值,就是分割出来的串使得这些串的字典序都小于答案的串的数量的最大值和最小值。如果最小值 <= k <= 最大值,显然就可以。
怎么求?可以DP。
因为一个分割点已经定了,所以很好求,i为第i个分割点,f(i) = min(f(j) + 1) 其中中间的串字典序不能大于答案。
考虑如何求这个字典序,可以用后缀数组SA求LCP,然后比较后面一位的大小,就可以O(1)弄
然后这个dp还需要一棵线段树来维护
就做完了
我们在大量细节中发现了少量的数据结构和DP
显然我目前我不想写这个东西
所以贴一下AQZ的代码,插个眼,想写了就来写
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
typedef std::pair < int, int > pai;
const int N = 200010;
const int M = N * 2;
const int inf = 0x7ffffff;
struct node {
int l, r, id;
} a[M];
int n, k, cnt, root, f[M], g[M];
char s[N], S[M];
namespace SA {
int sa[M], rk[M], tp[M], t[M], height[M], m, n;
int lg[M], st[30][M];
void Q_sort () {
for (int i = 1; i <= m; i++) t[i] = 0;
for (int i = 1; i <= n; i++) ++t[rk[i]];
for (int i = 1; i <= m; i++) t[i] += t[i - 1];
for (int i = n; i >= 1; i--) sa[t[rk[tp[i]]]--] = tp[i];
}
void _sort_ () {
for (int w = 1, p = 0; w <= n; m = p, p = 0, w <<= 1) {
for (int i = n - w + 1; i <= n; i++) tp[++p] = i;
for (int i = 1; i <= n; i++)
if (sa[i] > w) tp[++p] = sa[i] - w;
Q_sort();
std::swap(tp, rk);
p = rk[sa[1]] = 1;
for (int i = 2; i <= n; i++)
rk[sa[i]] = (tp[sa[i]] == tp[sa[i - 1]] && tp[sa[i] + w] == tp[sa[i - 1] + w]) ? p : ++p;
if (p == n) return ;
}
}
void intt() {
m = 26;
for (int i = 1; i <= n; i++)
rk[i] = S[i] - 'a' + 1, tp[i] = i;
Q_sort();
_sort_();
for (int i = 1; i <= n; i++) {
if (rk[i] == 1) continue;
height[rk[i]] = std::max(0, height[rk[i - 1]] - 1);
while (S[i + height[rk[i]]] == S[sa[rk[i] - 1] + height[rk[i]]]) height[rk[i]]++;
}
lg[0] = -1;
for (int i = 1; i <= n; i++)
lg[i] = lg[i >> 1] + 1;
for (int i = 2; i <= n; i++)
st[0][i] = height[i];
for (int i = 1; i <= lg[n]; i++)
for (int j = 2; j + (1 << i) - 1 <= n; j++)
st[i][j] = std::min(st[i - 1][j], st[i - 1][j + (1 << (i - 1))]);
}
int lcp (int l, int r) {
if (l == r) return n - l + 1;
l = rk[l], r = rk[r];
if (l > r) std::swap(l, r);
l++;
int k = lg[r - l + 1];
return std::min(st[k][l], st[k][r - (1 << k) + 1]);
}
}
int lcp (int l, int r, int x, int y = n * 2) {
int len = SA::lcp(x, l);
if (l + len > r) len = r - l + 1;
if (x + len > y) len = y - x + 1;
return len;
}
bool cmp (int l, int r, int x, int y) {
int len = lcp(l, r, x, y);
if (r - l + 1 == len || y - x + 1 == len)
return r - l + 1 <= y - x + 1;
return S[l + len] <= S[x + len];
} //S <= -> true
bool CMP (node x, node y) {
if (cmp(x.l, x.r, y.l, y.r) && cmp(y.l, y.r, x.l, x.r))
return x.id < y.id;
return cmp(x.l, x.r, y.l, y.r);
}
namespace Segment {
int min[M << 2], max[M << 2];
void update (int pos) {
min[pos] = std::min(min[pos << 1], min[pos << 1 | 1]);
max[pos] = std::max(max[pos << 1], max[pos << 1 | 1]);
}
void build (int pos, int l, int r) {
min[pos] = inf; max[pos] = -inf;
if (l == r) return ;
int mid = l + r >> 1;
build(pos << 1, l, mid);
build(pos << 1 | 1, mid + 1, r);
}
void modify (int pos, int l, int r, int x, int k, int op) {
if (l == r) {
if (op) min[pos] = k;
else max[pos] = k;
return ;
}
int mid = l + r >> 1;
if (x <= mid) modify(pos << 1, l, mid, x, k, op);
if (x >= mid + 1) modify(pos << 1 | 1, mid + 1, r, x, k, op);
update(pos);
}
int query(int pos, int l, int r, int x, int y, int op) {
if (x <= l && r <= y)
return (op ? min[pos] : max[pos]);
int mid = (l + r) >> 1, ans;
if (op) {
ans = inf;
if (x <= mid) ans = std::min(ans, query(pos << 1, l, mid, x, y, op));
if (y >= mid + 1) ans = std::min(ans, query(pos << 1 | 1, mid + 1, r, x, y, op));
} else {
ans = -inf;
if (x <= mid) ans = std::max(ans, query(pos << 1, l, mid, x, y, op));
if (y >= mid + 1) ans = std::max(ans, query(pos << 1 | 1, mid + 1, r, x, y, op));
}
return ans;
}
void print(int pos, int l, int r, int op) {
std::cout << l << ' ' << r << ' ' << (op ? min[pos] : max[pos]) << '\n';
if (l == r) return ;
int mid = l + r >> 1;
print(pos << 1, l, mid, op);
print(pos << 1 | 1, mid + 1, r, op);
}
}
bool DP (int x, int tmp) {
Segment::build(1, 1, n * 2 + 1);
Segment::modify(1, 1, n * 2 + 1, x + n, 0, 1);
Segment::modify(1, 1, n * 2 + 1, x + n, 0, 0);
for (int i = x + n - 1; i >= x; i--) {
//f[i]
int L = i, R = x + n - 1;
while (L < R) {
int mid = (L + R + 1) >> 1;
if (cmp(i, mid, a[tmp].l, a[tmp].r)) L = mid;
else R = mid - 1;
}
if (cmp(i, L, a[tmp].l, a[tmp].r)) {
f[i] = Segment::query(1, 1, n * 2 + 1, i + 1, L + 1, 1) + 1;
g[i] = Segment::query(1, 1, n * 2 + 1, i + 1, L + 1, 0) + 1;
} else f[i] = inf, g[i] = -inf;
Segment::modify(1, 1, n * 2 + 1, i, f[i], 1);
Segment::modify(1, 1, n * 2 + 1, i, g[i], 0);
}
if (f[x] <= k && k <= g[x]) return true;
else return false;
}
void print (int x) {
for (int i = a[x].l; i <= a[x].r; i++)
std::cout << S[i];
}
int work () {
int L = 1, R = cnt;
while (L < R) {
int mid = (L + R) >> 1;
if (DP(root, mid)) R = mid;
else L = mid + 1;
}
return L;
}
int main() {
std::cin >> n >> k;
std::cin >> (s + 1);
for (int i = 1; i <= n; i++)
S[i] = S[i + n] = s[i];
SA::n = n + n;
SA::intt();
for (int i = 1; i <= n; i++)
a[++cnt] = {i, i + n - 1, cnt};
std::sort (a + 1, a + cnt + 1, CMP);
root = a[1].l;
int aqz = a[work()].l;
cnt = 0;
for (int j = aqz; j <= n + aqz - 1; j++)
a[++cnt] = {aqz, j, cnt};
std::sort (a + 1, a + cnt + 1, CMP);
print(work());
return 0;
}
切题
在一个神秘的 JOSLFN 上,wzy 和 lqs2015 常年占据着切题榜的 rk1 和 rk2。现在他们在研究如何快速造题并验题。
分工是这样的:有 nn 个 wzy 负责造题,第 ii 个 wzy 会造出恰好 aiai 道题。有 mm 个 lqs2015 负责验题,第 jj 个 lqs2015 最多能验 bjbj 道题。每个 wzy 需要把他造的每一道题都给一个 lqs2015 来验。不过有一条限制,就是每个 wzy 的 aiai 道题必须给不同的 lqs2015 ,否则这个 lqs2015 会因为验到了来自同一个 wzy 的题而感到厌烦并且让所有 wzy 和 lqs2015 都消失。
在一旁瑟瑟发抖的 superay 想要知道,是否存在一种符合限制的验题的分配方案。
随着时间的推移,会有 qq 次对 a,ba,b 的修改。每次修改有如下四种:
1 i 表示将 aiai 加 11。
2 i 表示将 aiai 减 11。
3 j 表示将 bjbj 加 11。
4 j 表示将 bjbj 减 11。
superay 想知道每次修改之后还是否存在合法方案。
1e5级数据。
奇怪的建模第一次见
可能是我见识少了罢
有一个很显然的网络流建模
两方人放在左右,S向左部点连n条ai边,T向右部点连m条bi边,中间全部连满,跑最大流。
你就得到了10分的高分
场上我写到这里就把网络流扔了去想别的了
所以一无所获
然后40分做法是每一次操作直接改残量网络。
直接说正解。
最大流 = 最小割
那么满流就等价于
对于任意的 k ∈ [0, n],取前 k 个出题最多的人(从多到少排序)
意义:
左侧很显然,就是出的题数
右面的意义是
每个验题人 j 最多验 k 道题(因为每个出题人给他最多一题)
同时也不能超过自己的最大量
这就是意义,看起来挺显然的,但是我第一次看想了很久......
我们再设c_k表示满足 b_i >= k的个数,即自己能力大于等于最大接受题的人数,那么右面的式子就是
这个很显然
问题转化为了判断
是否对任意的k都成立,我们可以用线段树维护最小值
如何维护?具体地,对于12操作,从大到小维护ai,我们只需要寻找ai第一次/最后一次出现的位置,并加1或者减1。
对于34操作,只有c_{b_i} 及其相邻的两个位置会有变化,直接改
复杂度是n log n,由于我的唐诗操作多了一个log,但是问题不大
单身狗的复仇
小 D 是一只单身狗。他看到周围所有人都有了伴侣,心里十分不爽。于是他准备向这些情侣们展开复仇!
具体来说,小 D 周围有 n 个男生和 n 个女生,他们组成了 n 对情侣。
今天,这些情侣们排成了两排。男生们站在第一排,从左至右依次编号为 1…n;女生们站在第二排,从左至右依次编号为 1…n。形式化地说,存在一个 1,2,…,n 的排列 p₁,p₂,…,pₙ,使得第 i 个男生和第 pᵢ 个女生是情侣。
对于每一对情侣,小 D 想象他们之间有一根缘分的红线相连。我们用 (a,b) 来表示第 a 个男生和第 b 个女生之间的红线。
我们称两根红线 (a,b)、(c,d) 相交,当且仅当满足以下任意一个条件:
- a < c 且 b > d
- a > c 且 b < d
现在,小 D 要拆散这些情侣。他每次可以选择一对尚未被拆散的情侣 (i,pᵢ),并花费 wᵢ 的代价将他们拆散。与此同时,所有红线与 (i,pᵢ) 相交的情侣,也会被拆散(不需要花费额外代价)。
小 D 想要知道,拆散全部 n 对情侣所需的最小代价是多少。
首先将问题进行转换,把连线视为一个排列,男的是下标,女的是值,也就是输入的形态。
就将问题转化为了,排列中选出一些点(i,pi),让i和pi都递增,且按i排列后,相邻的两个点中,i <= pi。
有一个比较好象的n^2dp,可以拿到40分
我们想如何优化这个dp,可以用CDQ分治。
每次先处理mid左侧的答案,然后将左侧的往右侧转移,然后处理右侧的答案。
显然重点在如何转移上。
左侧点能否转移到右侧点关键在于中间能否再塞下一个点,如果能塞下,就不能转移。
可以先将这个区间内的点排序,然后求一下前屈,然后用一个栈求即可。具体实现可以看代码。
#include <bits/stdc++.h>
using namespace std;
const int INF = 2e9;
const int N = 2e5 + 5;
int a[N], p[N], f[N], c[N], n;
pair<int, int> b[N];
namespace SegmentTree {
int tr[N * 4];
void build(int l, int r, int node) {
tr[node] = INF;
if (l == r) return;
int m = (l + r) >> 1;
build(l, m, node * 2);
build(m + 1, r, node * 2 + 1);
}
void push_up(int node) {
tr[node] = min(tr[node * 2], tr[node * 2 + 1]);
}
void update(int l, int r, int pos, int node, int val) {
if (l == r) {
tr[node] = val;
return;
}
int m = (l + r) >> 1;
if (pos <= m) update(l, m, pos, node * 2, val);
else update(m + 1, r, pos, node * 2 + 1, val);
push_up(node);
}
int query(int l, int r, int ql, int qr, int node) {
if (ql <= l && r <= qr) return tr[node];
int res = INF;
int m = (l + r) >> 1;
if (ql <= m) res = min(res, query(l, m, ql, qr, node * 2));
if (qr > m) res = min(res, query(m + 1, r, ql, qr, node * 2 + 1));
return res;
}
}
stack<int> stk;
void cdq(int l, int r) {
if (l == r) return;
int m = (l + r) >> 1;
cdq(l, m);
int cnt = 0;
for (int i = l; i <= r; ++i) {
b[++cnt] = {p[i], i};
}
sort(b + 1, b + cnt + 1);
for (int i = cnt; i >= 1; --i) {
if (b[i].second <= m) continue;
while (!stk.empty() && b[i].second < b[stk.top()].second) {
c[stk.top()] = b[i].first; // C数组是前驱
stk.pop();
}
stk.push(i);
}
while (!stk.empty()) {
c[stk.top()] = 0;
stk.pop();
}
for (int i = 1; i <= cnt; ++i) {
if (b[i].second <= m) { // 当栈不为空且左半部分的当前下标大于栈顶元素
while (!stk.empty() && b[i].second > stk.top()) {
SegmentTree::update(0, n + 1, p[stk.top()], 1, INF);
stk.pop();
}
stk.push(b[i].second);
SegmentTree::update(0, n + 1, p[stk.top()], 1, f[stk.top()]);
} else {
f[b[i].second] = min(f[b[i].second], SegmentTree::query(0, n + 1, c[i], n, 1) + a[b[i].second]);
}
}
while (!stk.empty()) {
SegmentTree::update(0, n + 1, p[stk.top()], 1, INF);
stk.pop();
}
cdq(m + 1, r);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
freopen("revenge.in", "r", stdin);
freopen("revenge.out", "w", stdout);
cin >> n;
SegmentTree::build(0, n + 1, 1);
for (int i = 1; i <= n; ++i) cin >> p[i];
for (int i = 1; i <= n; ++i) cin >> a[i];
p[n + 1] = n + 1;
for (int i = 1; i <= n + 1; ++i) f[i] = INF;
cdq(0, n + 1);
cout << f[n + 1];
}
智慧树
小 M 在玩植物大战僵尸(β 版)。他把前六大关都通关了,现在需要让智慧树长到 1437 米才能解锁第七大关。智慧树是一棵有根树,根为 11 号节点,共有 nn 个节点。
由于智慧树生长得太慢,小 M 在给智慧树浇水的过程中感觉非常无聊。他注意到智慧树的每个叶子上长着一个 Peach(很合理,不是吗?),想把它们全部摘下来。
不过,小 M 注意到,由于 β 版 PvZ 中有很多颜色奇怪的豌豆(比如红色、蓝色、黄色、紫色),智慧树上的 Peach 也被污染成了非常丑的颜色。由于小 M 的一些特殊癖好,他认为每个 Peach 的颜色都必须是一个他指定的 [1,n][1,n] 内的整数(而你可以认为每个 Peach 的初始颜色为 n+1n+1),只有这样小 M 才会把它们一起摘下来。
幸运的是,我们有能力手动将 Peach 的颜色进行改变。具体地,在一次操作中,你可以准备一个豌豆射手和任意颜色的火炬树桩,射击某个节点,这样该节点的子树内所有叶子节点的 Peach 就能通过树枝木质部中的导管都被染成该颜色。小 M 可以依次进行任意次任意操作,最终每个 Peach 的颜色是最后一次被染的颜色,如果没有被染过,那就是初始颜色。
既然你这么智慧,请帮小 M 求出最少需要多少次染色操作才能让智慧树上所有叶子的 Peach 颜色为小 M 所指定的颜色。
首先考虑一个子树根节点的子树,如果根节点子树的根节点有c>=2的最大的c颜色相同,那么染根节点显然会让答案更小。
记 dpi,0 表示子树 i 没有被祖先节点预染色的最少操作次数。这样对于一个非叶子节点,首先将所有子树的 DP 值聚合起来,然后再决定在这个点是被提前染成什么颜色。
转移不难想
然后在节点i用一个map表示dp i,启发式合并,将小的子树map暴力插入,一个颜色如果在根和子树跟都出现就暴力更新,如果只在大的map中出现就需要更新,这玩意还得打一个标记来做。
四元组
给你一个nn个点的完全图,其中有mm条边是红色,其它边是蓝色
记f红色f红色表示四元组(i,j,k,l)的个数使得四个点之间所有边都是红色
记f蓝色f蓝色表示四元组(i,j,k,l)的个数使得四个点之间所有边都是蓝色
求f红色−f蓝色的绝对值
洛谷有原








 浙公网安备 33010602011771号
浙公网安备 33010602011771号