数据结构专题 6.23西安集训

[AGC015E] Mr.Aoki Incubator

假设时间无限大，那么所有点的位置顺序就是他们的速度顺序。也就是说，把他们按照速度排序，这个顺序就是最终顺序。对于两个点 $i$ ，$j$，如果 $v_{i}^{} > v_{j}^{}$ && $x_{i}^{}<x_{j}^{}$,或 $v_{i}^{} <v_{j}^{}$ && $x_{i}^{}>x_{j}^{} $,i就可以染j。进一步观察，我们发现一个点能染到的点是一个连续的区间 [L,R]（最重要的一句话），也就是说，我们可以用 O(nlogn)的时间预处理出每个点可以染到的区间。对于这个结论，我们可以以速度为 $x$ 轴。以初始位置为 $y$ 轴，建立平面直角坐标系，每个点的横坐标为速度，纵坐标为初始位置。简单分析会发现，只有关系为左上-->右下的点会相遇，那么两点相遇的时间就是 $\frac{X_{i}^{}-X_{j}}{V_{j}-V{i}} $，也就是说，两点连线，斜率为负，则两点会相遇，且斜率越大（也就是越平缓），相遇时间越早。

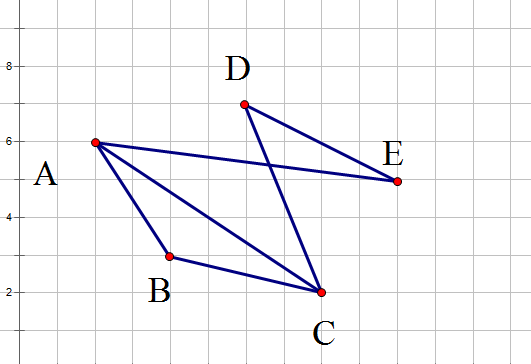
 对于上图来说，按时间顺序相遇的依次是AE，BC，DE，AC，AB，DC。（这些都属于直接相遇）

接下来我们考虑间接相遇。以DB两点为例，他们是不会直接相遇的，因为连线斜率为正。但是，他们都会与C相遇，且由于BC更平缓，所以B先与C相遇，C才与D相遇，因此，如果我们将B染色，就会通过C传到给D；给D染色则不行，除非B的左边还存在一个高于D的点F，F先与D相遇，F再与B相遇，将颜色传递给B，实现间接相遇。

 

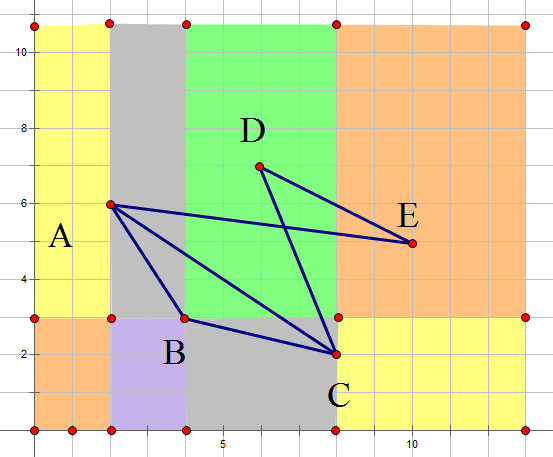
 假设A为可以直接与B相遇且速度最小的点，C为可以直接与B相遇且速度最大的点，那么，对于灰色区域的任意一点，我们可以让他直接与B相遇，完成直接染色；对于紫色区域的任意一点M，我们都可以让B先与A相遇，A与M再相遇，从而完成间接染色。对于绿色区域的任意一点M，我们都可以让B先与C相遇，C再与M相遇，完成间接染色。对于黄色区域，因为AC已经是速度最大或最小的能直接相遇的点，所以黄色区域里没有点；对于橙色区域中的点，既不能直接与B相遇，又不能找到中继完成间接相遇，因此无法被染色。综上，如果B点被染色，那么紫色，绿色，灰色内的点一定会被直接或间接染色，也就是说，对于速度在A，C之间的多有点，一定会被染色，而其他点一定不会被染色。

所以，我们只需要找到能与B直接相遇且V最小的，和能与B直接相遇且V最大的点，就能确定该点染色后能被染色的范围。而找这两个点是比较容易的，线段树二分，树状数组，或神奇的O（n）做法均可。

那么，此问题就被转化为子区间覆盖总区间的方案数问题。前人之述备矣，这里就不展开了。

 我们设 $dp_{i}^{}$ 表示考虑到第i个点，且i必选，覆盖区间 $[1,r_{i}]$ 的方案数，显然答案就是 $dp_{n+1}$ 而转移方程也很显然

 $dp_{i} =\sum_{j=1}^{i-1}dp_{j} (l_{i}-1 \le r_{j}) $

但是，直接转移的复杂度是 $O(n_{}^{2})$ 的，无法通过此题。但是，通过观察，我们发现，此题中的区间是满足一定单调性的。具体来说，如果 $j$ 满足条件，那么 $j+1,j+2......i-1$ 也必然也满足条件，也就是说，我们可以维护一下第一个满足转移条件的点，并利用前缀和，就可以在O（1）的时间内完成转移，dp的总复杂度为 O（n）。

总的时间复杂度为 O（n log n），瓶颈在于排序，离散化，求【L,R】

其实求区间也可以在O(n)的时间里完成，但是没啥必要

其实完全可以不用离散化，离散化的小细节卡了我好久...

取模之前一定要加上模数，这玩意卡了我将近半个小时

#include<bits/stdc++.h>
using namespace std;
const int N=5e6+5;
#define int long long
struct node{
    int x,v;
    bool operator<(const node&b)const
    {
        if(v==b.v) return x<b.x;
        return v<b.v;
    }
}a[N];
const int mod=1e9+7;
int pos[N],X[N];
int dp[N],sum[N],l[N],r[N],top,ans,n;
signed main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        scanf("%lld%lld",&a[i].x,&a[i].v);
        X[i]=a[i].x;
    }
    sort(a+1,a+1+n);sort(X+1,X+1+n);
    for(int i=1;i<=n;i++){
        a[i].x=lower_bound(X+1,X+1+n,a[i].x)-X+1;
        pos[a[i].x-1]=i;
    }
    for(int i=1;i<=n;i++){
        if(i==1) l[n-i+1]=pos[n];
        else l[n-i+1]=min(pos[n-i+1],l[n-i+2]);
        r[i]=max(pos[i],r[i-1]);
    }
    dp[0]=1;sum[0]=1;
    for(int i=1;i<=n;i++){
        while(l[i]-1>r[top]) top++;
        dp[i]=(sum[i-1]-sum[top-1]+mod)%mod;
        sum[i]=(dp[i]+sum[i-1]+mod)%mod;
    }
    while(n>r[top]) top++;
    ans=sum[n]-sum[top-1]+mod;
    ans%=mod;
    cout<<ans;
    return 0;
}

 

接下来是两道根号分治（我觉得更恰当的描述是一种基于根号性质的分类处理，尤其是当我们发现某一部分的值域在根号范围内时）

CF1039D You Are Given a Tree

由贪心可知，我们从叶节点向上遍历，如果遇到足够长的链就直接合并，复杂度 $O(n_{}^{2})$，显然无法通过此题。

但是，通过观察，我们发现答案一定是不上升序列。对于 $k \le \sqrt{n}$，此时我们可以直接搜索，复杂度 $O(n\sqrt{n})$；对于$k> \sqrt{n}$，我们知道答案一定是小于 $\sqrt{n}$ 的，且不上升。因此，我们考虑用类似 数论分块 的方法，枚举每一种答案，并二分这种答案所能包含的区间。这一部分复杂度是 $O(n\sqrt{n}\log_{}{n} )$。

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+55;
int cnt,head[N],fa[N],dfn[N],ans[N],n,m,B,tot,f[N];
struct edge{
    int to,nex;
}e[N];
void adda(int u,int v){
    e[++cnt].nex=head[u];e[cnt].to=v;head[u]=cnt;
}
void dfs1(int u,int fath){
    fa[u]=fath;
    for(int i=head[u];i;i=e[i].nex){
        int v=e[i].to;
        if(v==fa[u]) continue;
        dfs1(v,u);
    }
    dfn[++tot]=u;
}
int dfs2(int k){
    int res=0;
    for(int i=1;i<=n;i++) f[i]=1;
    for(int i=1;i<=n;i++){
        int u=dfn[i];
        if(fa[u]&&f[u]!=-1&&f[fa[u]]!=-1){
            if(f[u]+f[fa[u]]>=k){
                res++,f[fa[u]]=-1;
            }else{
                f[fa[u]]=max(f[fa[u]],f[u]+1);
            }
        }
    }
    return res;
}
int main(){
    cin>>n;
    B=sqrt(n);
    for(int i=1,u,v;i<n;i++){
        scanf("%d%d",&u,&v);
        adda(u,v);adda(v,u);
    }
    dfs1(1,0);
    ans[1]=n;
    for(int i=2;i<=B;i++){
        ans[i]=dfs2(i);
    }
    for(int i=B+1;i<=n;i++){
        int p=dfs2(i);
        int l=i,r=n,now=i;
        while(l<r-1){
            int M=(l+r)>>1;
            if(dfs2(M)==p){
                l=M,now=max(now,M);
            }else r=M;
        }
        while(i<=now){
            ans[i]=p;
            i++;
        }
        i--;
    }
    for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
    //9olgt
    return 0;
}

CF1446D2 Frequency Problem

首先有一个结论，答案子段的众数一定包含整个序列的众数，可以用反证法来证明。设整个序列众数为 $X$

因此，我们的任务就是找一个子段，使 $X$ 的出现次数与另一个数相同。最暴力的方法是枚举出现次数相同的那一个数 $Y$，复杂度是值域乘以长度。考虑优化。

设每个数的出现次数为 $cnt$，对于 $cnt_{i}\ge \sqrt{n}$ 的数，他们的种类 $\le \sqrt{n}$ 我们还是和上面的方法一样，枚举每一个这样的数，复杂度 $O(n\sqrt{n})$。而对于$cnt_{i}< \sqrt{n}$ 的数，我们发现他们种类很多，但出现次数 $\le\sqrt{n}$。因此，我们可以枚举他们的出现次数。具体来说就是 two_pointer 判断，复杂度也是$O(n\sqrt{n})$。

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+55;
const int inf=2e9+555;
int mxa,mp[N*4],mx,semx;
int n,m,cnt[N],a[N],ans;
int B;
int main(){
    cin>>n;
    B=sqrt(n);
    for(int i=1;i<=n;i++){
        cin>>a[i];
        cnt[a[i]]++;mxa=max(mxa,a[i]);
    }
    for(int i=1;i<=mxa;i++){
        if(cnt[i]>cnt[mx]){
            semx=mx;mx=i;
        }else if(cnt[i]>cnt[semx]){
            semx=i;
        }
    }
    if(!semx){cout<<0;return 0;}
    if(cnt[semx]==cnt[mx]){cout<<n;return 0;}
    for(int v=1;v<=mxa;v++){
        if(v==mx) continue;
        if(cnt[v]<=B) continue;
        for(int i=0;i<=n*2;i++) mp[i]=inf;
        mp[n]=0;
        int p=0;
        for(int i=1;i<=n;i++){
            int x=0;
            if(a[i]==mx) x=1;
            else if(a[i]==v) x=-1;
            p+=x;
            ans=max(ans,i-mp[p+n]);
            mp[p+n]=min(i,mp[p+n]);
        }        
    }
    for(int t=1;t<=B;t++){//two_pointers
        for(int i=1;i<=mxa;i++) cnt[i]=0;
        for(int i=1;i<=n;i++) mp[i]=0;
        int l=1,r=1;
        for(;r<=n;r++){
            mp[cnt[a[r]]]--;
            cnt[a[r]]++;
            mp[cnt[a[r]]]++;
            while(cnt[a[r]]>t){
                mp[cnt[a[l]]]--;
                cnt[a[l]]--;
                mp[cnt[a[l]]]++;
                l++;
            }
            if(mp[t]>=2) ans=max(ans,r-l+1);
        }
    }
    //l.igil.g
    cout<<ans<<endl;
    return 0;
}

下面是一段神奇的线段树题。首先，有关于线段树维护分界点/子序列，先看看 P3894。