为什么说浮点数的定义要谨慎?

关于浮点数的定义，可以使用float或double类型来定义32位或64位的长度。浮点数在计算机中的存储方式遵循IEEE 754 浮点数计数标准，可以用科学计数法表示为：

(S)1.M...*2^E

　　任一浮点数，是由符号（S）、阶码部分（E）、尾数部分（M） 这三个部分组成，float和double这两种浮点数在内存中的存储结构如下图：

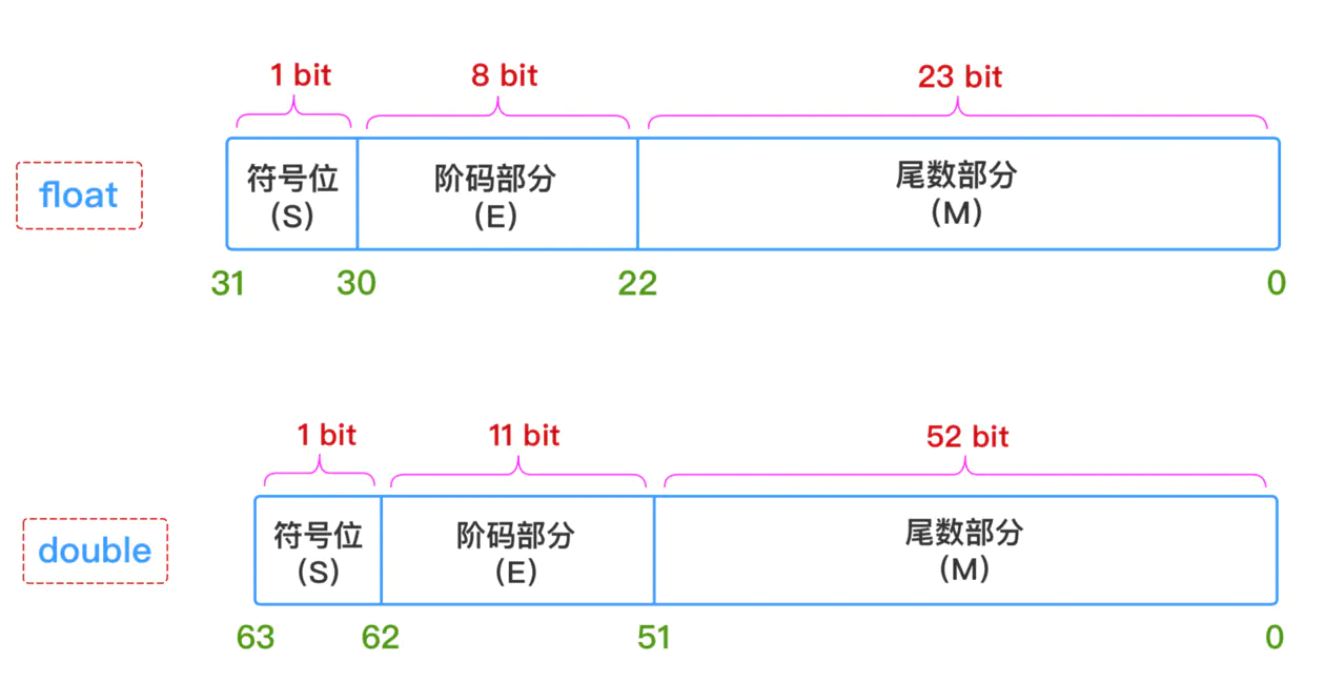
1、符号部分（S）
0-正 1-负

2、阶码部分（E）（指数部分）：

对于float型浮点数，指数部分8位，考虑可正可负，因此可以表示的指数范围为-127 ~ 128
对于double型浮点数，指数部分11位，考虑可正可负，因此可以表示的指数范围为-1023 ~ 1024

3、尾数部分（M）：
浮点数的精度是由尾数的位数来决定的：

对于float型浮点数，尾数部分23位，换算成十进制就是 2^23=8388608，所以小数点后的精度最多只有7位；
对于double型浮点数，尾数部分52位，换算成十进制就是 2^52 = 4503599627370496，所以小数点后的精度最多只有16位

 

对于如涉及金额等货币计算要求非常非常精确的计算时，就不能轻易的定义float或double进行运算，否则可能因精度丢失产生诡异的错误。此时可使用字符串或数组来定义长精度的数字，然后使用小学算术的四则运算逻辑进行逐位运算，总之就是要考虑借数、进位等问题，还是有点小复杂的。另外，在Java中的java.math名称空间下也提供如BigInteger和BigDecimal等高精度对象用于精确运算，使用时需注意效率问题。

 

 

 

本文部分内容参考自https://juejin.im/post/5e8fd75ef265da47bb70012c 版权归原作者所有