一句话题解（20180210~）

2.9

BZOJ 2006 [NOI2010]超级钢琴。这道题目几天之前就做了。做法是固定右端点，左端点在ST表上走，走法其实就是笛卡尔树的走法。完结撒花！

BZOJ 1218 [HNOI2003]激光炸弹。二维坐标系中给定n个整点，选择一个边长为r的端正的正方形内的点，问最大权值是多少。题目中点的范围只有5000，所以可以直接用前缀和暴力。如果点的范围更大，就必须得用扫描线做了。

2.10

UOJ 176 新年的繁荣。最小and生成树。使用了“玄学”做法，比较慢但是能AC。思路是分离0和1的集合，、

2.11

BZOJ 4568/ LOJ 2013 [Scoi2016]幸运数字。YYR、LK、ZXR、YJQ、XGG、TYH、DXQ他们那届的省选题目。树上的线性基合并，思路很简单但方法不少。合并两个线性基肯定是O(S²)的啊，不知道为什么neither_nor说可以O(S)……不过说，只有ST表和点分治能过，而点分治是真的快啊，只是我最开始点分治写错了，导致分下来点分树的深度不是15而是25还RE了……顺便吐槽一发BZOJ的速度……不过说，网上那些用其他方法AC的是怎么回事儿啊，最快的只有450ms又是什么鬼啊，本人尝试加了个已满不插反而更慢了……

	线性基总数	单次合并线性基	备注
树链剖分	O(n)	O(log2n)	会TLE
树链剖分2	O(n)	O(log n)	优化中间跳链过程，但并没有快依旧会TLE
倍增	O(nlog n)	O(log n)	会TLE
ST表	O(nlog n)	O(1)	AC
点分治	O(nlog n)	O(1)	AC，预处理时不需要合并线性基

 

	ST表	点分治	快了……倍
BZOJ 4568	48636 ms	8960 ms	5.428125
LOJ 2013	19152 ms	3592 ms	5.331849

2.16

BZOJ 2599 [IOI2011]Race。死活调不出来，与hzwer对拍了好几千组……后来找lydsy要数据，67组数据中只有3组卡了我，点开数据一看居然都是链，而且有一组数据长这样：n=10000，k=100，第i条边为(i,i+1)，所有边的边权或0或1，而一共只有199个1！愈加百思不得其解，终于发现有一个死角自己根本没有想到。就是说，如果现在的(sum,dep)比原来的优，它就应当覆盖那个桶么？其实不然。如果同一棵子树中有争奇斗艳，又该怎么办呢？这样就轻轻松松被卡了。而且链特别是那个奇葩数据尤其容易如此。

BZOJ 3697 采药人的路径。最开始的计数方法是有问题的，因为休息站可能在任何地方。需要注意的是，单根路径也需要特别考虑。另：不知道为何，稀里糊涂交上去就RANK 1了……

另：BZOJ 250题留念。且恰1500次提交（就多个1），800次AC。好巧啊……而且，1500/250和800/250似乎都大得没了谱了，可能这个样子也没谁了吧……

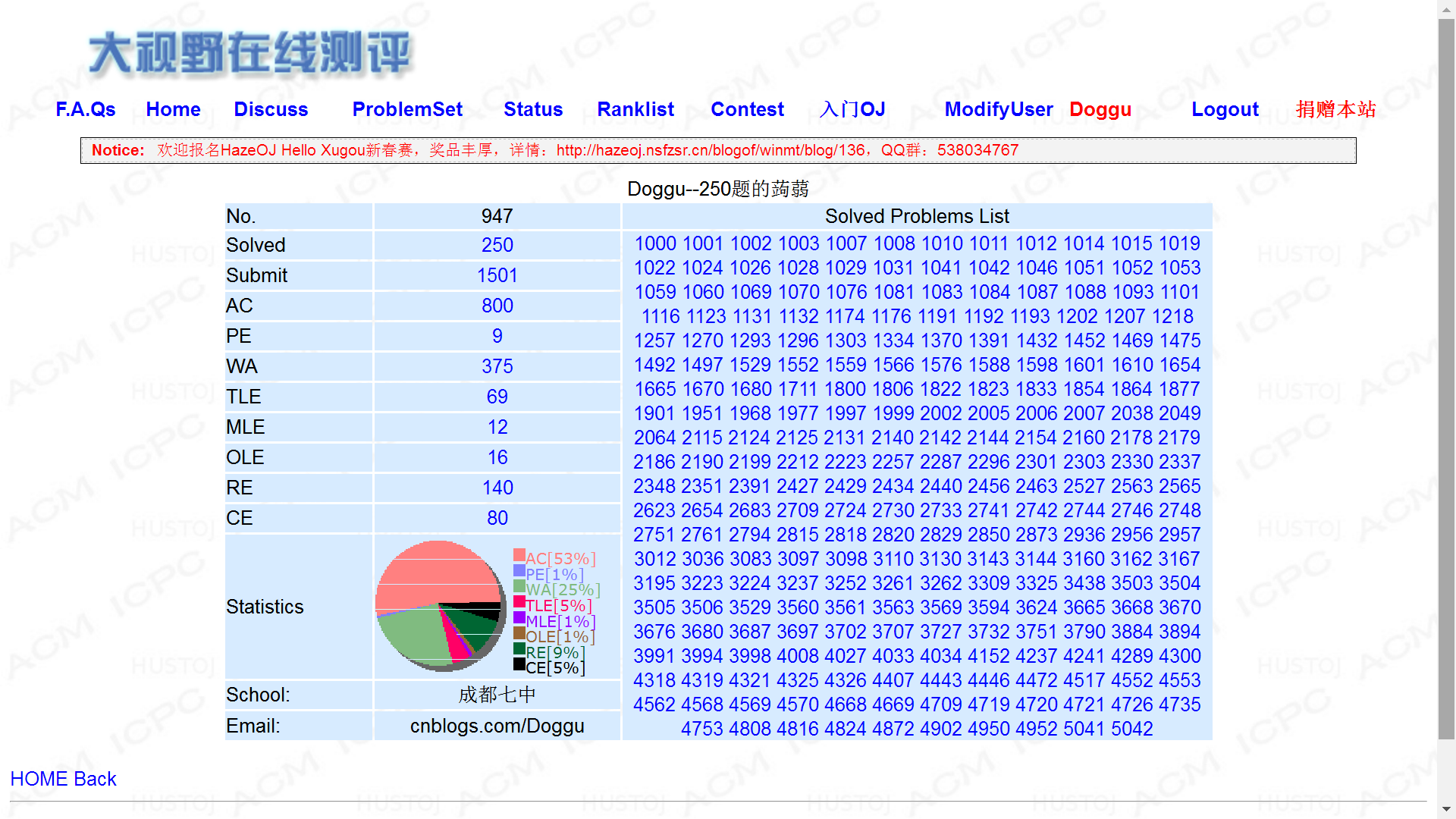
2.17

BZOJ 2152 聪聪可可。这道题最后需要除以gcd……静态点分当然是可以的，但是因为题目所求只有3，直接DFS原树枚举LCA信息很好往上传递。

BZOJ 3784 树上的路径。这题叫找带边权树上的m大路径并悉数输出。这是典型的第k优解问题，做法也就那么几种：二分，权值线段树/整体二分，字典序逐位走，使用相对偏序找出绝对偏序/强行构造。前三种做法常常可以适应k较大的情况，二分是限顶界，逐位走是分治，论来论去是很相似的。而这道题目使用的是第四种做法，通常k都比较小。思路上，和超级钢琴很像，加上点分治就很优秀了，时空复杂度皆为O(nlog²n)。hzwer说这道题用二分做也可以O(nlog²n)，最开始并不知道他在说什么，后来看了POJ 1741才明白……sort后使用2-pointer再减一减？但是因为减一减，可能会被卡……

BZOJ 4016 [FJOI2014]最短路径树问题。一千多msRE，TAT……后来发现自己根本是写错了，要求最大求成了最小……但是交上去还是一千多msRE，而hzwer学长则是600msAC。并不知道为什么，可能是BZOJ的栈太小了吧，但是我从lydsy那里要了数据本地只开8M的栈也是能过的啊……

2.18

BZOJ 4810 [Ynoi2017]由乃的玉米田。区间值域能否+出x，-出x，*出x。不带修改不强制在线，怎么办呢？能否+出x这个是有《等差子序列》的，除了树状数组还可以用正反bitset。*出x可以（或是只能）枚举因子（反正值域和序列长度、询问个数同阶），用值域桶或是可持久化值域线段树也能维护。但是-出x又该怎么办呢？这个用树状数组线段树平衡树都是较难维护的，但是bitset维护起来很容易。我们意识到，如果使用老式树据结构，要么套一套（可持久化=前缀和套），要么上莫队。而值域桶和bitset则只能依靠莫队且都可以O(1)滚动，最终空间复杂度O(N+M+V)，时间复杂度O(Nsqrt N+M*(N/64+log  N))。最后一个log N是概算，1e5内因子个数最多的是83160=2³*3³*5*7*11和98280=2³*3³*5*7*13，各有128个因子需枚举64次，就是4倍常数的log N辣。

BZOJ 4241 历史研究。这种可以用莫队做的题目，当然也可以用分块做辣！而且这样还可以支持强制在线！不过，本地测，分块的常数太大，OJ上也TLE了……另：觉得分块的题目划belong确实是一种很省事儿的方法，上次写modui频频被卡就是因为没有写belong边界情况判错了……

BZOJ 2038 [2009国家集训队]小Z的袜子(hose)。此题时限较宽，所以最终过了。但是还是很有些紧张，结合之前的题解列表如下：

Type	直接按照顺序做	无脑排序	分块排序	在线分块做法
Time	12228 ms	5680 ms	568 ms	3724 ms
Space	2592 kb			45648 kb

2.19

BZOJ 3236 [Ahoi2013]作业。T了很久都找不到缘由。wangyisong加强数据怎么着，网上都有用scanfAC的兄弟……2月25日一来一看，一眼就发现不对。sort的q应该是1~m，而我sort的是1~n，活该被卡。做法其实很简单，莫队+分块，因为分块可以O(1)单点修改O(sqrt)区间查询，复杂度就很优秀。LOJ那道6041的回滚莫队做法也是这样的。

BZOJ 1086 [SCOI2005]王室联邦。王室联邦分块，保证块个数、大小、直径，但不保证联通。因为分出来的是一整块或带个空点。但不知为何，DFS时u先压入stack和之后压入却是有区别的。

2.20

BZOJ 4034 [HAOI2015]树上操作。单点修改，子树修改，链询问。这道题之前是用树链剖分做的，后来用括号序线段树，当时后者没有AC因为有地方没开long long，现在又再写了DFS序树状数组。效率大致如此：

	树链剖分	括号序线段树	DFS序树状数组
Time	1916 ms	2348 ms	996 ms→668 ms
Space	12868 kb	17952 kb	8960 kb

2.21

BZOJ 4873 [Shoi2017]寿司餐厅。上一次这道题再怎么想都做不出，去了BS才发现自己学了假的最大权闭合子图。最大权闭合子图既不是什么+的连一边-的连一边，也不是所谓的任务连一边设备连一边，其实什么+-什么任务设施是没有实质区别的，两个极点其实是成立与否的不真即假的东西。中间每个点都可以看成一个命题，该命题连向一个极点的容量即是它跟同另一个极点的代价，而(u,v)的容量即是u跟源点v跟汇点的额外代价。最大权闭合子图并不能处理uv同跟一个极点的代价（如果有大概是“带权带花树”什么的），所以并不能想象成带权的2-SAT。而这道题目，所有的区间是一个点，所有的颜色是一个点。所有区间向汇点连-d（若d>0则换做从源点连d并sum+=d），大区间向小区间连INF，单点向其颜色连INF，且单点向汇点连x，其颜色向汇点连mx²，最后是sum-maxflow()。

另：当时考这道题的时候，并没有想到网络流。但看到n≤100，想到了堆瓶子的技能树。预处理之后用状压可以过n≤15的点，用递推可以过n≤100但m=0的点，最后只剩下3个n≤100且m=1的点，得了85分。

2.23

BZOJ 4773 负环。下午都在颓这一道题……上午写的乱搞枚举起点分层图DP，每层O(n)状态层间转移O(m)，最多层数O(n)，最坏复杂度O(n²m)，虽然可卡但是TEST和BZOJ都过了（加上卡时还可以过一些硬点）……下午先是跟yyf和jmr卡ZJC的二分答案迭代加深+DFSSPFA，但是w≤1000导致并跑不满指数级。不过说来，这种做法在BZOJ上跑得确实很快，虽然是有概率WA（并不知道怎么会WA）。而概率WA这件事情我最开始并不知道，整个人差点陷入癫狂，因为我的srand一直都没有变，而ZJC则是srand( ( unsigned long long ) new char );在禁掉clock()和time(0)的BZOJ上很优秀……不过正解是矩阵倍增Floyd，其实和分层图DP很像，不过是O(n)枚举起点*O(n)枚举答案*O(m)转移→O(log n)倍增出答案*O(n³)矩阵乘法，优的就是答案枚举复杂度。不过，二分+矩快是有问题的，因为多一个O(log n)。3种做法在BZOJ上的效率如下：

	分层图DP	倍增+矩阵乘法floyd	二分答案迭代加深+DFSSPFA
Time	1952 kb	4952 kb	2020 kb
Space	4812 ms	7688 ms	224 ms

2.24

BZOJ 4585 [Apio2016]烟火表演。这道题上下贯通，非常之妙……用f[u][i]表示修改u子树的边，使得u子树所有叶子到u距离皆为i的最小代价；用g[u][i]表示修改u子树的边和u连到父亲fa的边，使得u子树所有叶子到fa距离皆为i的最小代价。我们的思路是自下往上，先求出一个点u的f[u]数组，再通过f[u]数组和父子边权W求出g[u]数组，再将g[u]数组叠入f[fa]数组即可。如此，当我们考虑到点u的时候，它的f数组就已经统计出来，只不过要算出g[u]再融入f[fa]。这里有一个性质，f和g数组画成函数图象，则都是下凸的，而且斜率都是线性的。归纳法，若f[u]已下凸，考虑g[u]数组的形成，g[u][i]=min{f[u][j]+|(i-j)-W|}，稍作讨论即可知f与g的关系“斜率<0的地方上推W，斜率=0的线段右推W，补上斜率=-1与1的线段”，则g[u]显然是下凸的而合成的f[fa]也下凸。再考虑f的性质，可以发现f的截距为u子树边权之和，最右边直线斜率为u的儿子个数。如果我们一般化地维护拐点位置，含义是从此点之后直线斜率+1，多个拐点可以叠加。这样也可以倒推，切y轴直线的斜率即为d-拐点个数，整个凸包的形状也就得到维护。如是，则g[u]融入f[fa]也只需要直接将拐点合并。而f求g又如何呢？稍作观察，可以发现如果用堆维护拐点位置，只需弹出儿子个数-1个点，堆顶即为凸壳上凸部分的最左点，再弹堆顶则堆顶变成了凸壳最优区间的左端点，而显然该部分斜率为0。我们把这两个点都弹掉，于是只剩下了斜率<0地方的拐点，上推拐点位置不变，而原先最优区间的两个拐点则是右移了一段距离。考虑最后的答案如何得到，最后的f[1]的截距就是ΣW，而弹掉了1儿子个数的点，那现在的堆顶就是凸壳最优区间的左端点。考虑到现在堆中每一个点的贡献就是它的位置了。

而这道题目就这么完了么？当然没有，基本一样只有合并方式不一样，各种可并堆的效率还是有不少区别的。

	左偏堆切片树（比有效dep大小堆）	siz左偏堆（比siz大小堆）	斜堆	siz加权随机堆	1/2概率斜堆（完全随机堆）
Time	6936 ms	7216 ms	5844 ms	17468 ms	10040 ms

2.25

BZOJ 2049 [Sdoi2008]Cave 洞穴勘测。这道题目，之前已经写过2遍题解了。第一遍11.27，那时刚会LCT；第二遍1.9，听说了玄学可卡的并查集维护树形态+提根，之后就去写了“BZOJ 3237 [Ahoi2013]连通图”。3237可以用线段树分治做，这道题目也一样，而且跑得还不慢（至少比LCT快），但是因为栈调用，空间还是比LCT大3.43倍的，而LCT则比并查集大3.09倍。

	LCT	玄学可卡并查集	线段树分治
Time	1792 ms	348 ms	1452 ms
Space	2776 kb	896 kb	9524 kb

 

BZOJ 3339 Rmq Problem & 3585 mex。询问区间的mex，使用线段树进行合并是比较困难的。我们可以考虑莫队，则有一个全局桶涉及O(nsqrt)次单点修改与O(m)次查询。这个桶如果分块，则可以O(1)单点修改O(sqrt n)查询，和BZOJ 3236几乎一样。而这两道题目唯一的区别是序列中数的值域范围不同，离散化？NoNoNo！直接无视掉太大的数就行了。

不过，BZOJ上的这两道题，Hzwer还给出了线段树O(nlog n)的做法，和基站选址很像。就是说，我们可以for一遍，预处理出所有r的1~r的SG值。之后将l向右推进，考虑l~r与l+1~r的SG值到底有什么区别。就是说，如果l+1~r之间有l的值，则其SG值不变。如果没有，则SG值与l的值取个min。预处理出每个点的后继，使用线段树，区间修改削值单点查询即可（左端点预先排好序）。不可差分的东西用树状数组是不行的。两者效率如何，以BZOJ 3339为例。

	莫队+分块	递推+线段树
Time	11752 ms	668 ms
Space	6368 kb	11788 kb

Codeforces 940F Machine Learning。单点修改，询问区间mex。带修改莫队，l和r按n^2/3分块，然后按t排序，执行时先将l和r对位再将t对位。这样，关于t就会进行O(n^1/3*n^1/3)次O(n)的移动，关于l和r就会进行O(n)次O(n^2/3)的移动，共O(n^5/3)次单点修改，O(m)次查询，使用分块维护全局桶则是O(n^5/3)的复杂度，n=1e5的情况下4s还是够的。第一次写带修莫队，手脚还略显笨拙。交上去最开始TLE了，因为我的大块开的是(int)(pow(n,2/3)+0.5)，看似正确实际上2/3=0。后来又WA了，因为离散化后最多会有2*N个数字，然而我只开了N的数组，而且Codeforces上数组越界并不会RE……

BZOJ 1095 [ZJOI2007]Hide 捉迷藏。这道题有三种做法：动态点分，括号序列，树链剖分。

动态点分则需要3种可删堆，堆个数O(n)，空间O(nlog n)。单点修改涉及到O(log n)的分治区域，每个分治区域都涉及堆的操作，故时间复杂度为O(nlog²n)。3种堆分别如此：C[u]表示u的分治区域到其分治父亲距离的集合，B[u]表示u的各分治儿子到u的最大距离（即各分治儿子的C[u]堆顶）且若u为黑点塞入0，A表示各分治区域过分治根的最大路径（各个u的B[u]的堆顶两个之和）。询问时直接询问A堆顶，修改时先修改u自己的B处理如果过u的A的贡献，然后每层处理出C以及对分治父亲的B的影响，使用ST表可以O(1)查询距离。

括号序列也是一个很妙的做法。写出括号序列，可以发现两点之间的路径所过点与距离都可以与两点对应括号间的括号对应。使用线段树进行合并就可以方便地查询了。

树链剖分只有jiry_2会，正在申请中……

	动态点分+堆	括号序列线段树	树链剖分(jiry_2)
Time	7580 ms	2872 ms	5196 ms
Space	83712 kb	22736 kb	41044 kb
Code Length	4686 B	3222 B	4257 B

2.26

BZOJ 2388 旅行规划。分块+凸包。给区间加上一个等差数列，给区间加上一个值，询问区间最大值。这个东西使用线段树和平衡树很难update，那就不update。使用分块，考虑如何给一整个块加上一个等差数列。发现可以打标记k&b表示一条线，之后便可加上每个点的原值aa来查询单点。但如何询问一个块的最大值？如果列出式子，移项后可以发现，要让截距最大，要用-k[block]来切割这些(i,aa[i])，选切到的第一个点。这个于是可以使用凸包维护，修改时若修改一整个块则动k&b，若修改部分点则动aa并将整个块重构凸包。询问时，部分点可以直接查询，一整块则可以在凸包上二分到最优点再查询。如果块的大小是S，则修改复杂度为O(S+n/S)，询问复杂度则是O(S+n/S*logS)。

 

而调试这道题目的时候，犯了一些不可言说的错误。例如，求凸包时已经定位到块a却依旧调用belong[a]*S+1~belong[a]*S+S，二分的时候带入的是+k[block]。不过整体还好，提交就AC了。

 

不过，S的大小也是有讲究的。明显当S~n/S*logS时答案最优，但是我之前算错了S=sqrt(n*log2(n))就非常慢，S=sqrt(n)则快上不少，后来又算错了S(S²logS~n)慢了一些，再之后算出了正确的S(S²/logS~n)却也挺慢。并不知道为什么sqrt(n)最快，可能这就是理论与实际的些许差别吧。我sqrt的排到了rank 3，然而并不知道自己前面那两个CDQZ&THU学长是怎么干的，我的空间只有2416 KB而他们则高达16352 KB，难不成是线段树……

S=	sqrt(n*log2(n))	sqrt(n)	S2logS~n	S2/logS~n
Time	34380 ms	13456 ms	17616 ms	27516 ms
n=1e5时块大小	1287	317	121	1000
n=1e5时块个数	87	317	827	100

BZOJ 3005 体育课。和BZOJ 2388几乎一样。不过多了交换两个位置，只需要先把真实值都存下来，再各自加上真实值的差量即可。

3.1

　　感觉好久都没有做过题了啊……初七（22号）回来，考了2天试。之后搞了3天DS，27号开始搞MA，第一天看了一天的模方程，之后28号休息（颓）了一天，3月1号做了一些模方程的题目，3月2号看完了MYY的“再探FFT”并写了一篇学习笔记，3月3号考试并交流。

BZOJ 1420 Discrete Root / 1319 Sgu261Discrete Roots。已知k, a, 大质数p，求x ^ k=a (mod p)的所有根[0,p)。IDY的modlog的简化版，该题更普通的版本是BZOJ 2219 数论之神。我少特判了a=0的情况，此时若k=0则有x=0否则无解。之后，就可以求出p的原根g，有indx*k=inda (mod P-1)成立。之后就变成了一元一次同余方程（二元一次不定方程）。

BZOJ 2693 jzptab。觉得这题跟BZOJ 2154 Crash的数字表格没什么不一样的。为什么过不了呢……

BZOJ 3122 [Sdoi2013]随机数生成器。这题还好，只是特判很多。最后一个地方是+1在括号内或括号外会影响0和P的正确性。综合性挺强的。

Codeforces 360D Levko and Sets。这题真的非常优秀。以为想到原根就完了，没想到把阶和循环节那套理论也扯进来了，最后还调和级数容斥，实在是一波激起一波浪。

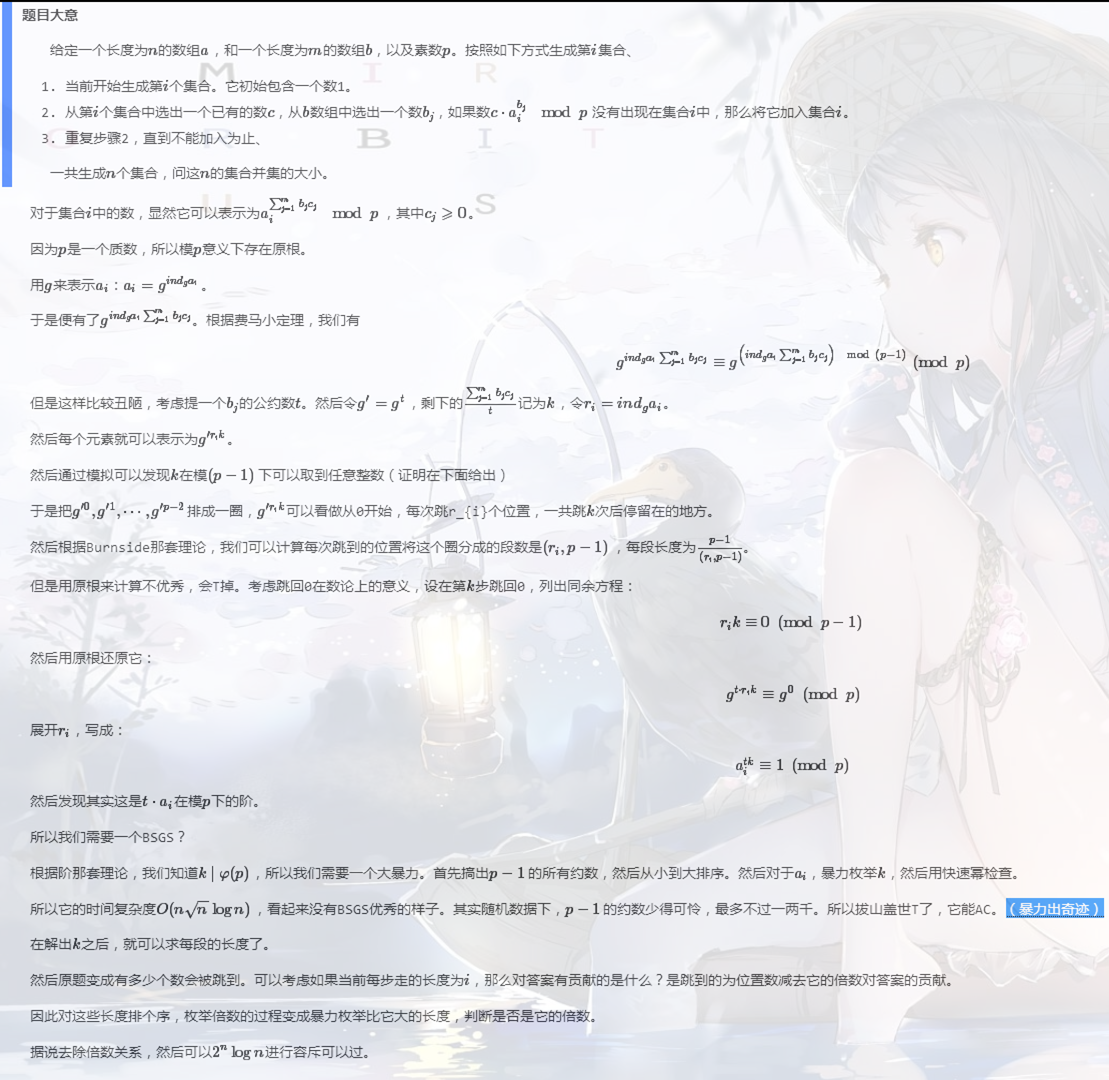
一些基础东西的证明：

3.4

BZOJ 5120 / LOJ 2321 [2017国家集训队测试]无限之环。YJQ讲过：N*M的网格图，每个格子的四个方向都有可能有一个插头。每次可以选择一个格子旋转90度，方向任意。求最少的旋转次数，使得不会有插头对着空气。当时ta并没有给出题号，只说这是一道清华集训的题目，出题人在临考之前才发现直线型管道有锅，临时修改才成事。因为是网格图，而且插头相对的就是在网格图上的边相邻，很容易想到二分图染色。每个点再定义内部费用，很好定义但写起来确实又臭又长。我的做法是把15种管道归纳至5种情况（5*2=10）并适当旋转，但犯了一个Naive的错误，直线型管道要么不转要么转1次不过转1次的被我写成了2次。改正之后交上去，BZOJ上跑了15000ms+，LOJ上跑了7000ms左右，加上LLL和SLF也没有什么用。之后用ZKW，BZOJ上20000ms，LOJ上9000ms。霎时非常的迷乱，别人可以才100ms+啊！于是看了，学到了。ZKW费用流，先SPFA建出最短路图，之后再沿最短路图DFS增广，同样返回flow，cost中间计算，长得跟DINIC很像。但是，DFS的时候会很奇葩地出现环导致死循环。我的做法是SPFA建出最短路图后，多次DFS每次把vis数组清空保证一个点不会在一次DFS中多次访问（源汇点除外）。而优化的做法，是不每次清空vis数组，而是直接跑。如此，就快了几十倍。

3.5

BZOJ 1565 [NOI2009]植物大战僵尸。最大权闭合子图。这道题目很明显，每个点一个命题，表示自己是否被吃。中间的依赖关系（后排依赖前排，受保护位置被攻击位置依赖）建成INF边。样例很良心地把依赖环突出了出来，如果没有，可能真的想不到先tarjan找SCC，把这些相互接应开了挂的点指出来。这些RMB植物真的很恶心！

BZOJ 3774 最优选择。二分图染色，之后再连是非边。不可不说的是，这个和“BZOJ 1475 方格取数”很像。

3.7

BZOJ 4832 [Lydsy2017年4月月赛]抵制克苏恩。简单记忆化搜索。

BZOJ 1419 Red is good。简单DP。但卡空间需要滚动。保留六位小数不允许四舍五入有两种做法：1.减去5e-7后输出；2.乘上1e6成long long（不需要floor因为强转直接截尾），再除以1e6输出double或输出除以1e6的商和小数点和06化的除以1e6的余数。

BZOJ 1415 [Noi2005]聪聪和可可。记忆化搜索，模拟。先n次BFS预处理出两点距离，之后记忆化搜索。如果两点相同，那么0次；如果dis≤2，那么1次；否则至少有一个回合，就这么做就完了。不知道这道题目是否可以出卡人的数据，但这题肯定是拓扑的。因为每回合下来，猫鼠距离至少减少1（如果猫只走1步就有点玄了）。

3.8

BZOJ 3717 [PA2014]Pakowanie。状态压缩DP，90s的题最开始常数过大还TLE了……问题是有n≤24个不同大小的物品放进m个不同规格的背包里，最少需要的背包个数。很明显，我们最终选择的背包一定是前几个最大的，但是24个物品放进去的顺序会产生很大的影响。于是我们可以这样设计状态：f[S]表示状态为S的这些物品放进背包里至少要用几个最大的背包，最后一个占用了多少空间。这个可以很容易地比较优劣，每一次枚举最后一个放入就可以了。时间复杂度O(n*2^n-1)，空间复杂度O(2ⁿ)。

BZOJ 2216 [Poi2011]Lightning Conductor。因为函数图象是sqrt，画一画就知道有决策单调性了。可以使用单调队列维护，但是弹出队尾的时候必须二分一下，因为我比较傻，二分的边界乱写，问题十分严重为此整整调了一个晚上。而YYF使用的分治做法下午就AC了……写了单调队列之后，我也在10分钟之内写出了分治的做法……只有知道什么是苦才能懂得什么叫甜啊~~~

3.9

BZOJ 2091 [Poi2010]The Minima Game。吃饭的时候YYF说ta做了的题目，一道博弈。由于是两人想尽量拉大分差，而且贪心的考虑一定每一次都取前几个……但是想起来还是好复杂……怎么办呢？考虑把过程反着来！计算先手在还剩多少个数的时候所能拉最大分差，然后O(n²)的转移救出来了……可是n≤1e6怎么办啊？可以发现

3.10

BZOJ 2819 Nim。单点修改询问路径异或和，路径异或和可以差分且因为n≤5e5所以只能O(nlogn)转化为子树修改单点查询，又因为修改可差分能上树状数组。但是，需注意的一点是，(u,v)路径异或和=(u,1)异或和^(v,1)异或和^LCA的值。记得在YALI的NOI WC时，有一天陈彦儒跟我说，胡一淳犯了很不可饶恕的错误……求路径异或和用LCA！胡一淳居然……但是，路径异或和确实要求LCA哈哈哈哈哈哈。

3.12

BZOJ 4131 并行博弈。典型的组合游戏。考虑一个游戏的SG值如何定义，稍微找一找规律可以发现，SG或为1或为0，(1,1)为1时SG为1，(1,1)为0时SG为0……因为每一次操作都一定会让(1,1)的值改变。最后异或起来就出了结果。然而为什么我没有看出来……

BZOJ 1435 [ZJOI2009]多米诺骨牌。执行过程很恶心但写起来其实还好（只要头脑清晰调试不出锅），为了避免出锅先照着STD敲了一遍，AC之后再自己敲一遍。但第二遍还是出现了一些问题，例如中间的插头DP那块STD是逆推的，而我写顺推时才意识到这一点。最后容斥的时候，什么时候配+1什么时候配-1也是很要命的问题。这道题目在17年2月CKY考状压的时候就见过了，只觉得是一道超级大神题。前几天在想的时候一直想的是把跨行放进状压里，处理出n行若干列的放置情况最后再列上容斥。现在再看当然知道不行了，因为单是n行若干列跨行就必须自己跨行，但现在若干块在一起就只需要挑一个跨行就可以了。这样的二维容斥……预处理出方方正正一块的DP值，之后一维暴力2^M容斥，另一维DP处理（很像WXH'S Road），处理的时候必须若干块绑在一起看。空间复杂度为O(2^M+N²M²)，时间复杂度O(N²Σ(M+1-i)i*2ⁱ+2^M*N²*M)。

BZOJ 4571 [Scoi2016]美味。可持久化trie可以处理x^区间ai求max的问题，但是这道题要求处理的是x^(区间ai+b)求max的问题。怎么办呢？考虑可持久化trie的原理，就是从高位逐步定到低位能凑1就凑1点集越来越小的过程。而现在要加一个b，怎么办呢？我们可以惊喜的发现，当高位一定时这一位又要取1，那么值域中灵活的就只有后面的那些位了，这刚好是一段连续的值域，加减同一个数后还是一段连续值域，所以就可以用主席树解决了。每个询问要在主席树里面找log次，复杂度O(Qlog²V)。

BZOJ 4567 [Scoi2016]背单词。觉得题意好迷……WA了好几遍才知道题目是什么意思。就是说，给你若干个字符串，让你重新排顺序，假设是字符串Si后缀的集合为Ai，若Ai中的串有排在Si后面的则要付出n*n的代价，否则需要付出x-y的代价，x指Si的位置，y指Ai中最靠后的位置。不难发现，这形成了一棵树的结构，通过反向往trie加入串我们能够轻松得到这棵树的结构（把空串也当作串）。如果对这棵树进行DFS，显然最后代价和≤n*(n+1)/2，所以n*n就相当于禁止。现在问题就变成了，对树进行DFS重标号，所有儿子到父亲标号之差的和最小是多少。考虑现在对u的子树进行重标号，问题可以拆成对v的子树进行重标号，调整对儿子v的访问顺序。很容易能够发现其中的无后效性。我们可以直接按v子树的大小来排序，小的排前面就像排队接水一样。另外，这题正着来直接用AC的fail树来构树也是可以的。

BZOJ 4361 isn。那天WYS做这道题目的时候，卡了好久好久的常数，最后还是没有卡过ccz181078，当了一个rank 2。记得当时他还说，ccz怎么做到的我360ms他居然284ms卡不过啊！结果今天我做这道题目，第一发交上去8msWA，非常痛苦于是差错最后发现只是少了一个%MOD……交上去跑得飞快，就当了RANK1了。但光说这道题目，还是很优秀了。我们要删若干个数，直到序列非降为止，问方案数。考虑最后序列有i个数，如果没有“直到……”，那么方案数=长为i的非降序列个数*(n-i)!，但是很有可能在有更多数的时候停下来。考虑如果之前不停下来，删删删到最后i个数，一定经历过长为i+1整个序列非降的时刻，而那时刻的每一种方案再任意删一个数就是i个数了，如此考虑刚好不重不漏。容斥啊！

3.14

BZOJ 3620 似乎在梦中见过的样子。既可以暴力O(n)次KMP，就像动物园那样维护一个“一半”指针；也可以使用后缀数组，然后枚举左端点再枚举LCP的起始点，最后会得到若干合法的区间，这并不需要使用什么高端数据结构（连折叠并查集也不需要），只需要在序列上差分只要值>0就是可行的右端点了。

3.15

BZOJ 4199 [Noi2015]品酒大会。据说是IDY跪倒MHY笑傲天地的题目，据说当时一个写了后缀数组一个写了SAM，然后一个写挂了……其实不管带不带M，都是在模拟后缀树。其实并不难，就在后缀树的结点进行相应的更新，最后f[i]再更新f[i-1]就行了。但是，要特别注意反串SAM的后缀树中每个叶子对应哪个后缀。

BZOJ 4974 [Lydsy八月月赛]字符串大师。用KMP的fail数组构造最小原串，和BZOJ 3325 [Scoi2013]密码（用Manacher的pal数组构造最小原串），BZOJ 4319 cerc2008 Suffix reconstruction （用SA/RANK数组构造最小原串），还有BZOJ 4104 [Thu Summer Camp 2015]解密运算（BZOJ 1031 [JSOI2007]字符加密Cipher的数组构造原串，JRY在WC2017上《通信题与数据压缩算法》所讲的Burrows Wheeler transform） 凑成了一组题目。这类题目其实就是根据数组找到原串一些位置字符的相等不等偏序关系，然后构造一个串出来。

？？？BZOJ 2754 [SCOI2012]喵星球上的点名。

3.17

BZOJ 4445 [Scoi2015]小凸想跑步。半平面交第一题。考试的时候一共4个半小时把4个小时都gang在上面，最后实在不想写“ax+by+c≥0”的直线转化式子，一分都没有，其实根本不复杂，只是可能调试特别特别犯。

BZOJ 2618 [Cqoi2006]凸多边形。改一改就是啦。

3.18

HDU 5325 Crazy Bobo。此题挺精妙的，要在树上找到最大的联通块，使得连接权值相邻的两点u,v的道路中任意节点x的权值都比u,v的小。稍作归纳推理，题目的要求就是找到一个联通块，使得从权值最小的点出发，然后不断访问权值渐渐增大的点，所经过的都是已经访问过的点。就是说，我们按权值不断放入点，联通块始终是联通的，就是说把权值最小的当成根，然后儿子的权值都比父亲大。那这样，思维就很显然了。我们可以把树的无向边钦定成有向边，使得永远是权值更小的点指向权值更大的点，然后我们只需要把每个点能够到达的点的个数取个max就可以了，这个显然可以记忆化搜索（因为满足拓扑序），就解决了。

3.20

BZOJ 2642 Pku3968 Jungle Outpost。二分答案+半平面交，因为这是个量变产生质变的东西。至于怎么check？不可能把所有的方案都弄出来，那就选k个连续的点，因为选了这些直线，<k个连续的点的直线都没有用了，而任何不连续的都可以变成若干连续的交，就解决了。

3.21

BZOJ 1115 [POI2009]石子游戏Kam。阶梯NIM。

3.25

BZOJ 2743 [HEOI2012]采花。离线+树状数组。

3.29

BZOJ 4641 基因改造。简单KMP，比较前驱，使用hash亦可。

3.30

BZOJ 1090 [SCOI2003]字符串折叠。区间DP。转移分3种，其实很好想。一，中间切断另开新段+M；二，结尾几个直接暴力输出来，以便前面的重复输出来；三，对中切断后半部分直接用前面的+R。只是我太傻了，第三种转移要求前半部分不再另开新段，于是就需要再加一个bool变量。这就应该结束了，但是我居然只改了记忆化搜索的函数而没有动数组。

BZOJ 1068 [SCOI2007]压缩。区间DP。转移更好想，因为不会有前面什么存下来的操作。只是，我实在是……枚举循环节的长度却不for到1处理数字时还直接把循环节长度扔进去……还有，第一发交的时候太急，居然调试用的while(true)都没有去掉，这道题只有10s却给了我一种卡OJ的即视感。

未完待续……