BZOJ 3529 [Sdoi2014]数表

3529: [Sdoi2014]数表

Description

    有一张N×m的数表，其第i行第j列（1 < =i < =礼，1 < =j < =m）的数值为能同时整除i和j的所有自然数之和。给定a，计算数表中不大于a的数之和。

Input

    输入包含多组数据。
    输入的第一行一个整数Q表示测试点内的数据组数，接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。

Output

    对每组数据，输出一行一个整数，表示答案模2^31的值。

Sample Input

2
4 4 3
10 10 5

Sample Output

20
148

HINT

1 < =N．m < =10^5  ， 1 < =Q < =2×10^4

Source

Round 1 Day 1

---

 

　　对于这种套路题，似乎已无什么新意，在此粗粗列举一下。

　　BZOJ 1968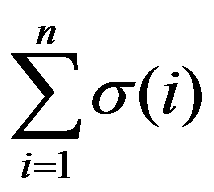  

　　BZOJ 2005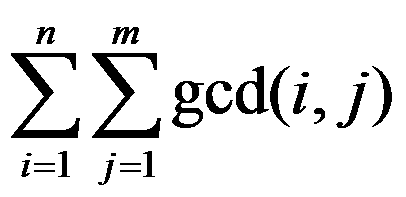 

　　BZOJ 2301（1101） 再加上区间的加加减减

　　BZOJ 3309 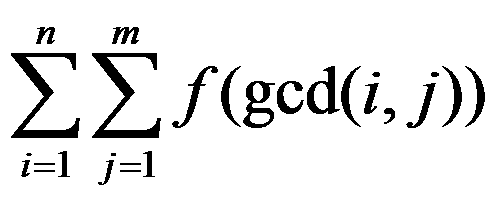 f(n)指n所含质因子的最大幂指数

　　BZOJ 2820

　　BZOJ 4407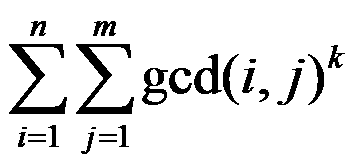

　　BZOJ 2693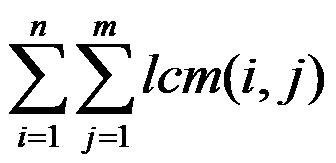 

　　BZOJ 3994 

　　我们可以大致发现，这种题目通常就是先展开，再收缩，最后算一下替代品。中间十足充分的利用了性质，就可以做出一道题。做这种题常常会令人心旷神怡，只是因为太难出，所以似乎并不能常常出现在OI赛场上。

　　但是，对于这种题目，如果能充分理解并掌握，那么你就会很好地理解整数到底意味着什么，整除到底意味着什么。如果这时候还能有一本《组合数学》打辅助，数论应该就没有什么问题了。

　　在这样的推导之中，我们常常用到这个式子。

　　这个式子的意义极其重大，因为如果会推这个式子，还知道积性函数是什么，那么就能秒掉不少题了。

　　对于这道题，我们就是要算出。但是，题目要求，第i个询问中算数的，这就需要离线了。我们把询问排个序，保证之后就可以搞了。随即把所有的与预处理出来，然后把sigma数组排个序，之后处理每个询问。这样，每个sigma就会一个个的加入我们的统计结果，毕竟是调和级数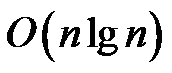。因为在加入时只会影响d的倍数，而我们查询时需要计算前缀和，这就可使用树状数组。

　　至此，这道题就算完了。因为mod那个神奇的数，所以只需要在最后ans&0x7fffffff就好了。

/**************************************************************
    Problem: 3529
    User: Doggu
    Language: C++
    Result: Accepted
    Time:3488 ms
    Memory:3308 kb
****************************************************************/
 
#include <cstdio>
#include <cstring>
#include <algorithm>
const int N = 20000 + 50;
const int RANGE = 100000;
struct DATUM {
    int n, m, a, id;
    bool operator<(const DATUM &rhs) const {
        return a<rhs.a;
    }
}data[N];
std::pair< int, int > sigma[RANGE+100];
int ans[N], mu[RANGE+100], minpa[RANGE+100], BOUND;
 
int prime[10000], ptot;
bool vis[RANGE+100];
void init_sigma() {
    mu[1]=1;sigma[1].first=1;
    for( int i = 2; i <= BOUND; i++ ) {
        if(!vis[i]) prime[++ptot]=i, mu[i]=-1, sigma[i].first=i+1, minpa[i]=i;
        for( int j = 1; j <= ptot; j++ ) {
            if((long long)i*prime[j]>BOUND) break;
            vis[i*prime[j]]=1;
            if(i%prime[j]==0) {
                mu[i*prime[j]]=0;
                if(i==minpa[i]) sigma[i*prime[j]].first=sigma[i].first+minpa[i]*prime[j];
                else sigma[i*prime[j]].first=sigma[i/minpa[i]].first*sigma[prime[j]*minpa[i]].first;
                minpa[i*prime[j]]=minpa[i]*prime[j];
                break;
            }
            mu[i*prime[j]]=-mu[i];
            sigma[i*prime[j]].first=sigma[i].first*sigma[prime[j]].first;
            minpa[i*prime[j]]=prime[j];
        }
    }
    for( int i = 1; i <= BOUND; i++ ) sigma[i].second=i;
}
 
int aa[RANGE+100];
void add(int pos,int val) {for( int x=pos; x<=BOUND; x+=x&-x)aa[x]+=val;}
int query(int pos,int val=0) {for( int x=pos; x; x-=x&-x )val+=aa[x];return val;}
 
int last=1;
void solve(int a) {
    while(sigma[last].first<=a) {
        int val = sigma[last].first, pos = sigma[last].second;
        for( int i = pos; i <= BOUND; i+=pos ) add(i,val*mu[i/pos]); 
        last++;
    }
}
 
int main() {
    int T;scanf("%d",&T);
    for( int i = 1; i <= T; i++ ) {
        scanf("%d%d%d",&data[i].n,&data[i].m,&data[i].a), data[i].id=i;
        if(data[i].n>data[i].m) std::swap(data[i].n,data[i].m);
        BOUND=std::max(BOUND,data[i].n);
    }
    init_sigma();
    std::sort(data+1,data+T+1);
    std::sort(sigma+1,sigma+BOUND+1);
    for( int i = 1, n, m; i <= T; i++ ) {
        n = data[i].n, m = data[i].m;solve(data[i].a);
        if(n>m) std::swap(n,m);
        for( int a = 1, ed; a <= n; a=ed+1 ) {
            ed=std::min(n/(n/a),m/(m/a));
            ans[data[i].id]+=(n/a)*(m/a)*(query(ed)-query(a-1));
        }
    }
    for( int i = 1; i <= T; i++ ) printf("%d\n",ans[i]&0x7fffffff);
    return 0;
}