GM(1,1) GM(2,1)
import numpy as np
import pandas as pd
data0 = r'G:\WECHAT\WeChat Files\wxid_op0z9xixesag22\FileStorage\File\2023-02\data.csv'
data = pd.read_csv(data0)
# 描述性统计分析
# description = [data.min(), data.max(), data.mean(), data.std()] # 依次计算最小值、最大值、均值、标准差
# description = pd.DataFrame(description, index = ['Min', 'Max', 'Mean', 'STD']).T # 将结果存入数据框
# print('描述性统计结果:\n',np.round(description, 2)) # 保留两位小数
# 代码6-2
# # 相关性分析
# corr = data.corr(method = 'pearson') # 计算相关系数矩阵
# print('相关系数矩阵为:\n',np.round(corr, 2)) # 保留两位小数
# 代码6-3
# 绘制热力图
import matplotlib.pyplot as plt
# import seaborn as sns
# plt.subplots(figsize=(10, 10)) # 设置画面大小
# sns.heatmap(corr, annot=True, vmax=1, square=True, cmap="Blues")
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# plt.title('相关性热力图')
# plt.show()
# plt.close
from sklearn.linear_model import Lasso
#
# lasso = Lasso(1000)
# lasso.fit(data.iloc[:,0:13],data['y'])
# print('相关系数为:',np.round(lasso.coef_,5))
#
# print('相关系数非零个数为:',np.sum(lasso.coef_ !=0))
# mask = lasso.coef_ !=0
# print('相关系数是否为0:',mask)
#
# mask = np.append(mask,True)
# outputfile = r'G:\data\data\new_reg_data.csv'
# new_reg_data = data.iloc[:,mask]
# new_reg_data.to_csv(outputfile)
# print('输出数据的维度为:',new_reg_data.shape)
import sys
#('G:\data\data\code')
from GM11 import GM_1_1
from Gm21 import predict
# GM = GM_1_1()
# data1= r'G:\data\data\new_reg_data.csv'
# new_reg_data1 = pd.read_csv(data1)
# new_reg_data1.index = range(1994,2014)
# new_reg_data1.loc[2014] = None
# new_reg_data1.loc[2015] = None
# new_reg_data1.loc[2016] = None
# cols = ['x1','x3','x4','x5','x6','x7','x8','x13']
# print((new_reg_data1.loc[range(1994,2014),'x1'].values))
# for i in cols:
# GM.set_model(new_reg_data1.loc[range(1994,2014),i])
# # print(GM.predict(1)[0])
# # print(GM.predict(2)[1])
# new_reg_data1.loc[2014,i] = GM.predict(1)[0]
# new_reg_data1.loc[2015,i] = GM.predict(2)[1]
# new_reg_data1.loc[2016,i] = GM.predict(3)[2]
# new_reg_data1[i] = new_reg_data1[i].round(2)
# outputfile1 = r'G:\data\data\new_reg_data_GM11.xls'
# y = list(data['y'].values)
# y.extend([np.nan,np.nan,np.nan])
# new_reg_data1['y'] = y
# # new_reg_data1.to_excel(outputfile1)
# print('预测结果为:\n',new_reg_data1.loc[2014:2016,:])
data1 = r'G:\data\data\new_reg_data.csv'
new_reg_data1 = pd.read_csv(data1)
new_reg_data1.index = range(1994,2014)
new_reg_data1.loc[2014] = None
new_reg_data1.loc[2015] = None
new_reg_data1.loc[2016] = None
cols = ['x1','x3','x4','x5','x6','x7','x8','x13']
for i in cols:
print(i)
data21 = np.array((new_reg_data1.loc[range(1994, 2014), i]))
predict_data = predict(data21)
result = np.ediff1d(predict_data)
print('原数据:', data21[:])
print('预测结果:', result)
# # print(GM.predict(1)[0])
# # print(GM.predict(2)[1])
new_reg_data1.loc[2014,i] = result[len(result)-1]
new_reg_data1[i] = new_reg_data1[i].round(2)
for i in cols:
print(i)
data21 = np.array((new_reg_data1.loc[range(1994, 2015), i]))
predict_data = predict(data21)
result = np.ediff1d(predict_data)
print('原数据:', data21[:])
print('预测结果:', result)
# # print(GM.predict(1)[0])
# # print(GM.predict(2)[1])
new_reg_data1.loc[2015,i] = result[len(result)-1]
new_reg_data1[i] = new_reg_data1[i].round(2)
for i in cols:
print(i)
data21 = np.array((new_reg_data1.loc[range(1994, 2016), i]))
predict_data = predict(data21)
result = np.ediff1d(predict_data)
print('原数据:', data21[:])
print('预测结果:', result)
# # print(GM.predict(1)[0])
# # print(GM.predict(2)[1])
new_reg_data1.loc[2016,i] = result[len(result)-1]
new_reg_data1[i] = new_reg_data1[i].round(2)
outputfile1 = r'G:\data\data\new_reg_data_GM21.xls'
y = list(data['y'].values)
y.extend([np.nan,np.nan,np.nan])
new_reg_data1['y'] = y
new_reg_data1.to_excel(outputfile1)
print('预测结果为:\n',new_reg_data1.loc[2014:2016,:])
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR
inputfile = r'G:\data\data\new_reg_data_GM21.xls' # 灰色预测后保存的路径
data = pd.read_excel(inputfile) # 读取数据
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13'] # 属性所在列
data.index = range(1994,2017)
data_train = data.loc[range(1994,2014)].copy() # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std # 数据标准化
x_train = data_train[feature].values # 属性数据
y_train = data_train['y'].values # 标签数据
linearsvr = LinearSVR() # 调用LinearSVR()函数
linearsvr.fit(x_train,y_train)
x = ((data[feature] - data_mean[feature])/data_std[feature]).values # 预测,并还原结果。
data['y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y']
outputfile = r'G:\data\data\new_reg_data_GM21_revenue.xls' # SVR预测后保存的结果
data.to_excel(outputfile)
print('真实值与预测值分别为:\n',data[['y','y_pred']])
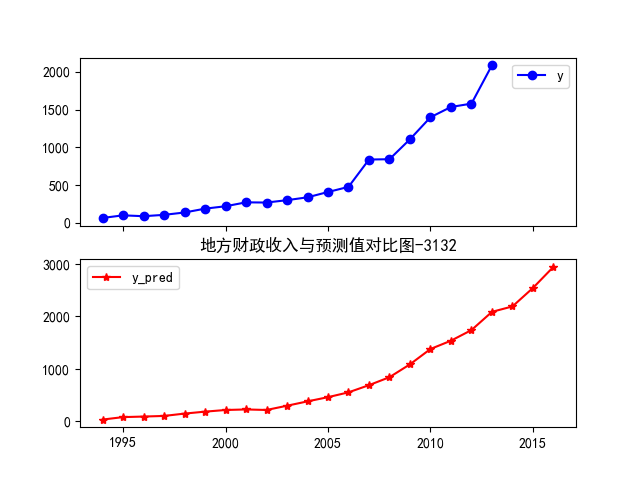
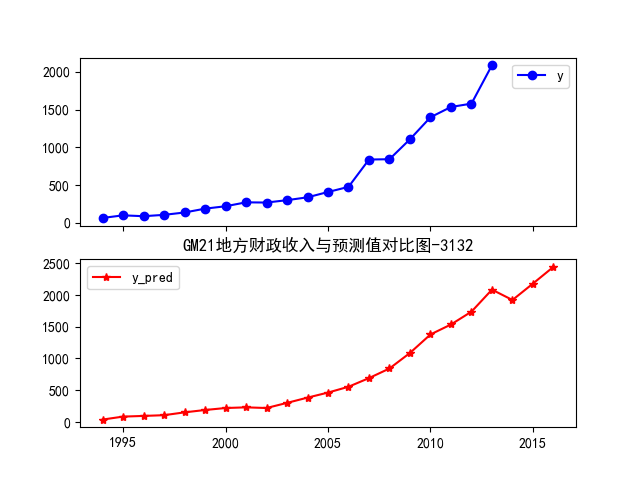
fig = data[['y','y_pred']].plot(subplots = True, style=['b-o','r-*']) # 画出预测结果图
plt.title('GM21地方财政收入与预测值对比图-3132')
plt.show()
GM(1,1)
import numpy as np
import matplotlib.pyplot as plt
class GM_1_1:
"""
使用方法:
1、首先对类进行实例化:GM_model = GM_1_1() # 不传入参数
2、使用GM下的set_model传入一个一维的list类型数据: GM_model.set_model(list1)
3、想预测后N个数据:GM_model.predict(N)
想获得模型某个参数或实验数据拟合值,直接访问,如:GM_model.modeling_result_arr、GM_model.argu_a...等
想输出模型的精度评定结果:GM_model.precision_evaluation()
"""
def __init__(self):
self.test_data = np.array(()) # 实验数据集
self.add_data = np.array(()) # 一次累加产生数据
self.argu_a = 0 # 参数a
self.argu_b = 0 # 参数b
self.MAT_B = np.array(()) # 矩阵B
self.MAT_Y = np.array(()) # 矩阵Y
self.modeling_result_arr = np.array(()) # 对实验数据的拟合值
self.P = 0 # 小误差概率
self.C = 0 # 后验方差比值
def set_model(self, arr: list):
self.__acq_data(arr)
self.__compute()
self.__modeling_result()
def __acq_data(self, arr: list): # 构建并计算矩阵B和矩阵Y
self.test_data = np.array(arr).flatten()
add_data = list()
sum = 0
for i in range(len(self.test_data)):
sum = sum + self.test_data[i]
add_data.append(sum)
self.add_data = np.array(add_data)
ser = list()
for i in range(len(self.add_data) - 1):
temp = (-1) * ((1 / 2) * self.add_data[i] + (1 / 2) * self.add_data[i + 1])
ser.append(temp)
B = np.vstack((np.array(ser).flatten(), np.ones(len(ser), ).flatten()))
self.MAT_B = np.array(B).T
Y = np.array(self.test_data[1:])
self.MAT_Y = np.reshape(Y, (len(Y), 1))
def __compute(self): # 计算灰参数 a,b
temp_1 = np.dot(self.MAT_B.T, self.MAT_B)
temp_2 = np.matrix(temp_1).I
temp_3 = np.dot(np.array(temp_2), self.MAT_B.T)
vec = np.dot(temp_3, self.MAT_Y)
self.argu_a = vec.flatten()[0]
self.argu_b = vec.flatten()[1]
def __predict(self, k: int) -> float: # 定义预测计算函数
part_1 = 1 - pow(np.e, self.argu_a)
part_2 = self.test_data[0] - self.argu_b / self.argu_a
part_3 = pow(np.e, (-1) * self.argu_a * k)
return part_1 * part_2 * part_3
def __modeling_result(self): # 获得对实验数据的拟合值
ls = [self.__predict(i + 1) for i in range(len(self.test_data) - 1)]
ls.insert(0, self.test_data[0])
self.modeling_result_arr = np.array(ls)
def predict(self, number: int) -> list: # 外部预测接口,预测后指定个数的数据
prediction = [self.__predict(i + len(self.test_data)) for i in range(number)]
return prediction
def precision_evaluation(self): # 模型精度评定函数
error = [
self.test_data[i] - self.modeling_result_arr[i]
for i in range(len(self.test_data))
]
aver_error = sum(error) / len(error)
aver_test_data = np.sum(self.test_data) / len(self.test_data)
temp1 = 0
temp2 = 0
for i in range(len(error)):
temp1 = temp1 + pow(self.test_data[i] - aver_test_data, 2)
temp2 = temp2 + pow(error[i] - aver_error, 2)
square_S_1 = temp1 / len(self.test_data)
square_S_2 = temp2 / len(error)
self.C = np.sqrt(square_S_2) / np.sqrt(square_S_1)
ls = [i
for i in range(len(error))
if np.abs(error[i] - aver_error) < (0.6745 * np.sqrt(square_S_1))
]
self.P = len(ls) / len(error)
print("精度指标P,C值为:", self.P, self.C)
def plot(self): # 绘制实验数据拟合情况(粗糙绘制,可根据需求自定义更改)
plt.figure()
plt.plot(self.test_data, marker='*', c='b', label='row value')
plt.plot(self.modeling_result_arr, marker='^', c='r', label='fit value')
plt.legend()
plt.grid()
return plt
GM(2,1)
def predict(data):
a_x0 = np.ediff1d(data).T
B = np.array([-data[1:], np.ones([len(data) - 1])]).T
Y = a_x0
u = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Y)
a, b = u[0], u[1]
return [(b / (a * a) - data[0] / a) * math.exp(-a * i) + b / a * i + (1 + a) / a * data[0] - b / (a * a)
for i in range(len(data)+2)]
GM(1,1)
GM(2,1)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号