2023.6 做题记录
6.1
[ICPC2022 Xi'an R] Tree
标签:线段树,长链剖分
来源:ICPC2022 Xi'an R
写了个非常丑陋的 \(O(nlogn)\),线性的正解移步lg题解区吧。
令 \(dep_i\) 为点 \(i\) 的深度,其中 \(dep_1=1\),不难发现答案最多是叶子数量与最大的深度取 \(min\),这时因为每个叶子剥一条到根链出来一定可以覆盖这棵树,把同一层的所有点放在一个集合也可以覆盖这棵树。
然后我们考虑怎么样调整答案,考虑一个贪心,每次找到当前深度最大的叶子,然后剥去这个叶子到根的链,已经填过的集合数量+1,然后根据当前的叶子数量和最大深度更新答案,不难通过调整法证明其正确性。
剥去链可以通过均摊删除的方法,如果往上暴力删除的过程中发现某个祖先之前已经被删掉了,根据我们的操作这个祖先上面的点也一定被删掉了。
删掉一个点的时候需要把子树内还存在的叶子的深度-1,不难通过 dfs 序线段树实现。
复杂度是非常丑陋的 \(O(nlogn)\),有很多简单好写的线性做法。
[ICPC2022 Xi'an R] Bridge
标签:线段树
来源:ICPC2022 Xi'an R
假设我们先把这个 \(n\times (m+1)\) 的图建出来,连边 \((a,b) \rightarrow (a,b+1)\) 。
把每次的修改操作稍作变换,改为删掉 \((a,b) \rightarrow (a,b+1)\) 和 \((a+1,b) \rightarrow (a+1,b+1)\),连上 \((a,b) \rightarrow (a+1,b+1)\) 和 \((a+1,b) \rightarrow (a,b+1)\),这样修改后的图还是 \(n\) 条链,并且仍然符合题意。
我们给每个点 \((a,b)\) 初始标上颜色 \(a\),于是可以把修改操作看做交换两个链的一段后缀交换,查询某个链最后一个点的颜色。
这个可以用平衡树实现,但是又更好写的做法,考虑开 \(n\) 个动态开点线段树,用 \(std::map\) 维护每种颜色的出现位置(所属的链),所有线段树公用一个线段树就可以简单实现交换节点了。
具体的,考虑交换时先给会用到的节点 push_down,把颜色更新,交换后从下往上更新,在 push_up 时更新每个线段树节点的父亲,并清空除了叶子的点的颜色。
修改时先用 \(std::map\) 找到第一个小于要交换的后缀的点所在的链,然后不断跳父亲找到所属线段树的根,之后就可以做线段树上的操作了,暴力跳复杂度是线段树的树高,是 log 级别的。
于是时空复杂度都是 \(O(nlogn)\)。
还有很多操作分块的 \(O(n\sqrt n)\) 做法,值得学习一下。
6.8
【UR #25】见贤思齐
标签:倍增
来源:UR#25
思路来自zak神仙的题解,补充一些自己口胡的证明。
记 \(f(x,i)\) 表示 \(i\) 时刻 \(x\) 的答案,因为受到 \(p_i\) 的影响,所以这个函数的取值有两种,一种是自己增加,即为 \(a_x+i\);一种来自 \(p_i\),即为 \(f(p_x, i-1)+1\),不难得到两种要取最小值,因为要考虑初值 \(a_x\),所以我们可以写出这样的计算 \(f(x,i)\) 的式子:
这个 \(+i\) 看上去不太好处理,不放设 \(g(x,i)=f(x,i)-i\),上式可以变为:
直接求出所有 \(g\) 是困难的,但是观察所有的 \(g(x,i)\),不妨先忽视 \(i\) 这一维,然后把 \(a_x\) 记作常量 \(A_x\),同理记 \(a_x-i\) 为 \(C_x\),不难发现我们可以把 \(g\) 表现为分段函数的形式。
其中 \(y=p_x\) 。不妨再写一个 \(g(y)\):
做一个换元,为了简单,我们省去常量,只看 \(g(x)\) 与 \(g(z)\) 的关系。
观察到函数做换元后依然是形式相同的分段函数,这启示我们维护一个分界线 \(l,r\),初始 \(l\) 极小,\(r\) 极大,每跳一次,把 \(l\) 和 \(a_x-i\) 取最大,\(r\) 和 \(a_x\) 取最小,容易观察到当 \(l\geq r\) 时函数变为常量,直接计算即可。
注意特殊的一点是跳一次时 \(l\) 做过操作后需要先进行一次 \(l\geq r\) 的判断,这个是相当于先给 \(g(z)\) 做预判,如果 \(g(z)\) 的下界已经充分大,那么分段函数会提前变为常量。
这个可以简单倍增维护,复杂度 \(O((n+q)\log V)\)。
6.11
CF809E Surprise me!
标签:莫比乌斯反演,虚树
来源:树上问题作业
这题给我最大的帮助是让我学会了拆欧拉函数。
直接放结论:
证明可以参考这个
有这个结论就可以把 \(\phi(a_x,a_y)\) 拆出来,就好做多了。
然后一通推式子得到:
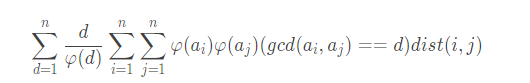
观察到有等于关系,不妨转化为整除关系。
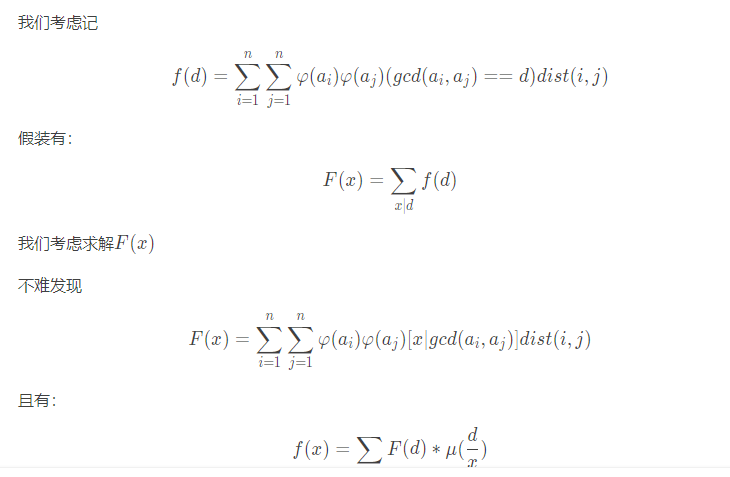
求 \(F(d)\) 可以把所有 \(d|a_x\) 拿出来建虚树,那么直接跑一个带权数点对的DP就可以了。
因为保证点权是排列,所以建虚树的总点数是调和级数级别 \(O(nlogn)\),所以虚树的复杂度是 \(O(nlog^2n)\),其他的东西都是可以 \(O(nlogn)\) 做的,所以总复杂度 \(O(nlogn)\)。
6.13
CF1628E Groceries in Meteor Town
标签:kruskal 重构树,线段树
来源:树上问题作业
题目相当于求到所有白色点的瓶颈边,典中典 kruskal 重构树,转化为求所有白点和当前询问点的lca。
关于点集的lca的一个结论是点集中 dfn 最小和最大的点的 lca,证明可以考虑所求的点需要满足子树的 dfn 区间完整包含整个点集并且深度最大,不难发现这个结论求的点一定是符合要求的。
于是线段树维护当前白色点最小/大的 dfn 即可,修改是区间覆盖,特判一些无解的情况。
复杂度 \(O(nlogn)\)。
6.14
AT CF J Tree MST
标签:最小生成树,boruvka
来源:boruvka 练习
用这道题整理一下 boruvka 算法。
求 MST 的若干种算法中,最常见的是 kruskal,但是还有一种基于连通块的贪心算法叫做 boruvka,和 kosarajo 一样都是容易被遗忘但是在特殊的题中会有重要作用的算法。
对比一下 kruskal 和 boruvka,kruskal 是对边排序然后生成连通块,复杂度是 \(O(mlogm)\),而 boruvka 是对每个连通块求出对其他连通块的最优边,因为每做一次合并连通块会至少减少一半,所以复杂度是 \(O(mlogn)\)。
boruvka 的优势在于如果图有特殊性质并且边的数量非常大时,有时候并不需要把所有边都遍历一遍,所以特殊情况下 boruvka 的复杂度可能是 \(O(nlogn)\)。
例如这题,给出的图是完全图,kruskal 是很难做的,但是 boruvka 就相对简单一些。
考虑怎么样求出连通块间的最优边。先把题目的式子拆一下,变成 \(w_x+w_y+dis_x+dis_y-2dis_{lca(x,y)}\),现在重点在于解决 lca 的问题。
因为 boruvka 外层 while 循环会进行 \(O(logn)\) 次,所以只要我们中间计算最优边的过程复杂度是 \(O(n)\) 到 \(O(nlogn)\) 就比较合理。
考虑枚举 lca,我们可以预处理出子树内的最小的 \(w(y)+dis_y\),然后从上到下求出 \(x\) 的祖先们的最小的 \(y\) ,然后更新 \(x\) 所在连通块和 \(y\) 所在连通块的最优边。
但是问题在于如果 \(x\) 和 \(y\)z 在同一连通块就寄了,针对这种去重,一种巧妙的方式是记录一个次小值 \(y2\),满足 \(y2\) 和 \(y\) 不在同一连通块,这样就算 \(x\) 和 \(y\) 冲突了还有一个备选方案。
于是求最优边的复杂度是 \(O(n)\) 的(视并查集复杂度是常数),那么整体复杂度就是 \(O(nlogn)\) 的。
不过本题还是存在 kruskal 的做法的,下面这题大概是不存在 kruskal 只能用 boruvka 的。
20230613 NOI模拟赛T1
题意:给一个 \(n\) 个点的完全图,有 \(m\) 条特殊边给定权值,其他的边权定义为两个端点的差的绝对值(\(|x-y|\)),求最小生成树,\(n\leq 1e9,m\leq 1e5\)。
这 1e9 个点和大概 1e18 级别的边量肯定不能 kruskal,考虑用 boruvka。
boruvka 一个解题思路上的优点在于外层循环是 \(O(log点数)\),所以内层计算最优边可以设计相对暴力的算法。
不考虑特殊边,一定会选 1 到 2,2 到 3,等等这样一个边权为 1 长度为 \(n-1\) 的链,而且这个是非常优的,所以我们考虑离散化下来这 \(m\) 个特殊边的端点,端点之间的肯定是连成这样边权是 1 的链,我们接下来要做的就是把这些链之间找最优边然后合并。
考虑题目的边权是绝对值,在不考虑特殊边时肯定是向相邻的链连边最优,这个可以用链表维护向左/右第一个不在当前连通块的点解决。
剩下的就是特殊边,因为总边数是 \(m\),所以每个特殊边的端点暴力向两边拓展复杂度是均摊 \(O(m)\) 的,只需要判断不在同一个连通块中的点是否是自己连出来的特殊边的端点,如果是则继续借助链表跳。
这样内层是均摊 \(O(m)\) 的,因为初始一共有 \(O(m)\) 个连通块,所以最多合并 \(O(logm)\) 次,总复杂度 \(O(mlogm)\)。
6.15
[JOI Open 2022] 放学路
标签:点双,广义串并联图
来源:广义串并联图练习
感觉这题并不是广义串并联图的题,只能说操作有点相似罢了,应该说是点双好题。
广义串并联图的定义是没有同胚于 \(K_4\) 的子图的图,这题的图显然不是,但是部分分 \(m-n\leq 13\) 启发可以借鉴广义串并联图中的一些操作。
考虑是否能删去一些点使得删去点后的图等价,这里的等价表示为新图中最短路仍然存在,如果原图存在不同于最短路的路径,新图中也必须存在这样的路径,但可以不是原图中的那条。
首先1号点和 \(n\) 号点无论如何都不能删,考虑其他点,如果是1度点直接删掉没有影响,如果是2度点删掉后新边权为原来的边权和。
叠重边复杂一些,如果两条重边权值一样,那么叠起来没有影响,如果不一样,需要考虑一些额外的东西。
注意到一个部分分时保证整个图形成一个点双,假设现在叠重边的大环境是整个图是一个点双,那么两条边权值不同肯定代表存在不同于最短路的路径,直接判断有解。
现在仍然讨论一个点双的情况,我们不断重复上述操作直到不能再操作,考虑这时候如果点双内存活的点数 >3,那么肯定有解,证明如下。
因为不能继续广义串并联图的操作,所以点双内至少有4个点,那么图中一定至少有一个导出子图同构于下图
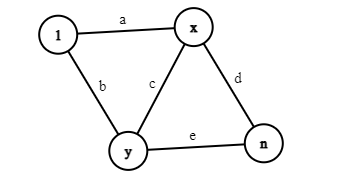
通过待定系数法解方程可以得出一定有解。
那么假如原图不是一个点双,考虑怎么样把原图变成一个等价的点双做上面的算法。
结论是直接加入无向边 \((1,n,dis)\),其中 \(dis\) 表示最短路长度。
感性证明考虑我们广义串并联图操作中删除的点集中的点 \(x\),如果存在 1 到 \(n\) 的简单路径经过 \(x\),那么新图中这条简单路径一定成环(必要性),如果 \(x\) 不属于新图中的点双,那么 \(x\) 到 1 和 \(n\) 所在的点双一定要经过一个割点,那么在原图中就不存在 1 到 \(n\) 经过 \(x\) 的简单路径(充分性)。
于是只需要维护删点操作即可,用 std::unorderd_map 之类的哈希表即可,复杂度 \(O(m*hash)\)。
6.17
[SNOI2020] 生成树
标签:广义串并联图
来源:广义串并联图练习
做了这题才认识到广义串并联图方法的强大。
如果只是仙人掌,显然答案是所有环长度之积,但是题目在仙人掌的基础上加上了一条边,传统的点双解法就要变得很麻烦了,而广义串并联图解决这个问题是简单的。
首先仙人掌加一条边还是广义串并联图,一定可以缩成一个点,这是因为如果不能的话说明图中存在同胚于 \(K4\) 的子图,容易发现不能通过仙人掌加一条边得到 \(K4\)。
所以要做的只有设计缩点和叠重边的操作,生成树计数问题考虑每条边的贡献,设 \(f_i\) 表示这条边出现在生成树上的方案数,\(g_i\) 为没有出现,这里的边可以是经过操作后缩合的边。
初始时,我们有 \(f_e=重边e的数量,g_e=1\),这是显然的。
缩一度点直接把 \(f_e\) 累乘到答案里面。
缩二度点需要考虑伸出的两条边不能同时不存在与生成树中,容易得出 \(f'_e=f_{e1}*f_{e2},g'_e=f_{e1}g_{e2}+g_{e1}f_{e2}\) 。
叠重边需要考虑两条重边不能同时存在生成树中,也容易得出 \(f'_e=f_{e1}g_{e2}+g_{e1}f_{e2},g'_e=g_{e1}*g_{e2}\)。
用hash表维护删点操作即可,用std::(unorderd_)map复杂度为 \(O(mlogm)\)。
6.18
CF650E Clockwork Bomb
标签:构造
来源:树上问题作业
简单构造题,难度虚高。
考虑如果不考虑最小化操作数,首先一定是有解的,具体的,可以给第二棵树每个点钦定一个父亲,然后dfs第一棵树,从叶子开始,如果这个点在第一棵树上的父亲不是第二棵树上的,就把这个边删掉,连出来这个点在第二棵树上到父亲的边,因为是从叶子开始所以不会出现第一棵树操作后产生环的现象,相当于强行钦定一个拓扑序。
先考虑操作数下界,显然是 \(n-1-same\),\(same\) 表示两棵树上相同的边数。
考虑一定可以构造到这个下界,具体的,可以提前把这些两棵树上相同的边缩成一个连通块,缩完点后再跑上述算法,注意一点是连通块的根需要设为连通块内在第一棵树上深度最浅的点,容易发现这样的点是唯一的,合并时新增的边的端点是并查集的根和他在第二棵树上的父亲。
复杂度是并查集复杂度,可以认为是 \(O(n)\)。
CF1383C String Transformation 2
标签:构造,状压DP
来源:树上问题作业(树上问题?)
很逆天的构造。
第一步转化是简单的,考虑给每种字符开一个节点,求按时间顺序添加若干条有向边的方案,使得对于每个位置的 \(A_i\) 和 \(B_i\),都存在一条加入时间递增的路径,下文称这个图是原图。
考虑构造一个图,仍然给每种字符开一个节点,直接连有向边 \(A_i\) 到 \(B_i\),下文称这个图是新图。
先考虑一种构造方法,跟弱连通块数和导出DAG子图大小有关,考虑把整个图划分为若干个弱连通块,每个弱连通块的问题独立,单独考虑一个的,设这个弱连通块的大小是 \(n\),最大导出DAG子图的大小是 \(m\)。
考虑把点重新标号,使得导出DAG的一个拓扑序是 1,2,……,\(m\),在原图按顺序连边 \((m+1,m+2),(m+2,m+3),……,(n-1,n),(n,1),(1,2),(2,3)……(m-1,m),(m,m+1),(m+1,m+2),(m+2,m+3),……,(n-1,n)\)。
容易发现除了DAG中的逆序顶点对,其他所有顶点对都存在一条时间递增的路径,我们一共加入了 \(2n-m-1\) 条边,回到整个图,答案就是总点数-最大导出DAG大小-弱连通块数。
感觉这个东西很优秀,于是考虑证明这是答案下界。
还是看每个弱连通块中的独立问题,考虑由这个弱连通块构造出来的原图中的点集起码也是个弱连通块,毕竟要考虑到弱连通块的定义。
考虑增量法构造,我们维护新图弱连通块的形成情况和导出DAG子图的情况,初始每个点都是独自一个弱连通块,原图中还没有加边,考虑在原图中每加一条边产生的变化。
若两端点现在不属于同一个弱连通块,那么把这两个块合并,块数-1,导出DAG子图大小不变。
否则,有可能现在成了一个环,为了保险起见,如果两个端点都在现在的导出DAG子图中,就移除掉其中一个,所以块数不变,导出DAG子图大小最多-1。
因为最终原图一定会形成一个弱连通块,所以第一种情况一定出现了 \(n-1\) 次,那么就有不等式 \(m\geq n-(e-(n-1))\),得到 \(e\geq 2n-m-1\),回到整个图中,就有 \(e\geq 2n-m-c\),其中 \(c\) 是弱连通块数。
于是做一个求最大导出DAG子图的DP就好,因为只有20种子图,所以 \(2^{|\sum|}|\sum|\) 的DP是可以接受的。
CF757G Can Bash Save the Day?
标签:边分治,线段树
来源:树上问题作业
虽然拆贡献是典中典,但是理论正解是边分治,用树剖+主席树逃课了。
把贡献拆成 \(dis_x+dis_y-2dis_{lca(x,y)}\),然后就可以3log做了,具体的,用树套树,外层序列,内层dfn,查询修改都是3log。
但是观察修改是形如交换序列相邻的元素,如果表示为前缀关系的话,只会影响到一个前缀信息,也就是第修改位置个,那么对应到表示前缀的主席树上,就只需要单独修改这一棵线段树就好。
然后就没了,但是这题卡常卡空间,借鉴了一些别人的技巧:
1 .区间修改使用标记永久化。
2 .定期重构所有的主席树来节省空间,实测重构 \(\frac{m}{3e4}\) 次就足够了。
值当是一道练习标记永久化和卡常技巧的题了,边分治dame。
6.19
[ARC162D] Smallest Vertices
标签:计数DP,prufer序列
来源:ARC162订题
没想到正解居然和prufer序列没多大关系。
首先一个结论是有度数限制的有根树个数是 \(\frac{(n-2)!}{(d_{root}-1)\prod_{i\neq root}d_i}\),证明就是裸的有根树prufer序列,只需要考虑最后一个元素一定是根即可。
1肯定在每个树中都满足要求,然后考虑所有度数为0的点也一定满足要求,所以这些点满足要求的树的个数都是上式,直接加起来。
下面的东西是我场上没想到的。注意:prufer序列很难表示一棵树的子树,所以遇到子树相关大概率要换一些别的计数方法了。
现在考虑所有 \(i>1\) 并且 \(d_i>0\) 的点 \(x\),假设确定了子树的点集是 \(s\),并假设这个点集 \(s\) 的度数限制可以保证存在生成树,那么可以分开计算,先算以 \(x\) 的子树的生成树个数,再把这棵子树缩成一个点,计算整棵树的生成树个数,有式子:
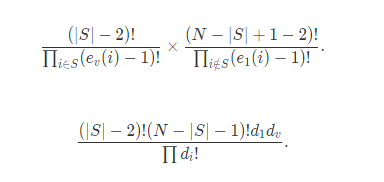
因为是要求子树内的点都大于 \(x\),所以倒着DP做一个背包,用 \(f_{i,j}\) 表示 \(i\) 个点度数和为 \(j\) 的方案数,复杂度 \(O(n^3)\),其他部分的复杂度都是 \(O(n)\) 或 \(O(n^2)\),所以总复杂度为 \(O(n^3)\)。
[ARC162E] Strange Constraints
标签:计数DP
来源:ARC162订题
思维难度不大的题。
没想到题解的第一步转化,原来的限制确实很"strange",考虑转化一下,设 \(d_i\) 表示 \(i\) 在 B 序列的出现次数。
首先肯定还是有 \(d_i\leq A_i\),接下来把考虑 \(d_{B_i}\leq A_i\) 转化为对于每种颜色 \(i\) 找到 \(d_i\) 个位置放置满足 \(d_i\leq A_i\)。
转化为放置问题就简单多了,考虑从 \(d_i\) 大的开始DP,设 \(f_{i,j,k}\) 表示考虑到 \(d_x=i\) 的所有颜色,已经填了 \(j\) 种颜色,用了序列的 \(k\) 个位置,转移枚举新增的颜色种类数 \(l\),有:
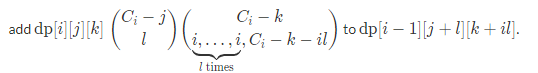
其中 \(c_i\) 表示 \(A_x\geq i\) 的个数。
看上去是 \(O(n^4)\) 的DP,实际上考虑当前枚举 \(i\) 时颜色种类数 \(j\) 一定有 \(j\leq \frac{k}{i+1}\),最坏的情况就是所有 \(k\) 个位置填的都是 \(d_x=i\) 的颜色,\(l\) 显然也是有界的,具体的是 \(l\leq \frac{n}{i}\)。
所以实际的计算量是 \(\sum_{i=1}^{n}n\frac{n}{i+1}\frac{n}{i}\),显然小于等于 \(n^3\sum_{i=1}^{n}\frac{1}{i(i+1)}\),右边裂项求和就是 \(\frac{n^4}{n+1}\),所以实际计算量是 \(O(n^3)\) 的。
6.23
CF1510J Japanese Game
标签:构造,贪心,枚举
来源:0623模拟赛
逆天模拟赛,不想写总结,但是题还是挺有意思的。
作为模拟赛考这题的时候是要求构造出一个合理解,虽然获得每个连续段的长度可以轻松构造出解。搬出题人下发了个std,试了一下居然是真的在检验方案的合法而不是单纯看一下输出是1的位置输入是否是1,很震惊,就开始逆向思考std是怎么写的,相当于如果知道连续段数量和每个的长度怎么知道解对不对。
一开始觉得是先把连续段尽量靠左放,再把连续段尽量靠右放,取个并集,但是被这样的连续段数组:n=10,p={4,2} 给 hack 掉了。
后来从本质出发,对于当前的连续段,把他之前的尽量靠左,之后的尽量靠右,这样就给他腾出来一片生存空间,然后在这个空间中他最靠左和最靠右的位置的交集就是一定被覆盖的位置。
有了这个结论就很显然可以给输入数组中的每个连续1段划分一个生存空间,问题就在于划分多大,以及如果原来就不存在生存空间的连续段不能忽视掉。
手玩一下发现长度为2和3的空白是可以通过在左边填满右边填1个来满足要求,任意长度 >3 的段都可以拆解为若干2和3的和,并且可以轻松证明他们之间是独立的,于是我上午的想法是让每个连续1段划分的生存空间尽量少,这样空白越大似乎越可能合法。
但是这样会面临一个难题:空白为0,也就是不存在空白时是合法的,但是空白是1是不合法的,就很难受。自己做卡在这里就不会做了。
正解比我想想的简单,因为每个连续1段连续划分的生存空间肯定不需要超过3,否则可以通过扣掉一些2和3来满足不超过3,那么只需要枚举所有的连续1段的生存空间即可,这个不超过3,并且直接要求所有连续1段的生存空间都是这个可以发现如果有合法方案一定可以枚举到。
所以再遇到难以讨论的情况,就试着通过转化成小规模的枚举问题来简化讨论量或者就不需要讨论了,有时候就可以化繁为简。
CF794G Replace All
标签:范德蒙德卷积,莫比乌斯反演,最大公因数
来源:0623模拟赛
先不考虑?的存在
首先考虑 \(a=b\) 的情况,不难发现这时候答案是 \(\sum_{i=1}^{n}2^i\)。
如果 \(a\neq b\),需要讨论 \(a,b\) 种两种字符的数量差。
先给一个结论,现在这种情况填的二进制串对 \((s,t)\) 一定满足存在一个循环周期 \(|c|\) 使得 \(s\) 和 \(t\) 是由若干个 \(c\) 拼接形成的,其中 \(|c|=\gcd(|s|,|t|)\)。
证明很多人说可以考虑字符串匹配过程是一个辗转相除的过程,就有结论是最大公因数,感性理解很对,记结论就完了。
现在假设 \(a\) 的字符A数量多 \(va\),\(b\) 的字符B数量多 \(vb\)。
分类讨论,如果 \(va=vb=0\),答案就是 \(\sum_{i=1}^{n}\sum_{j=1}^{n}2^{\gcd(i,j)}\),莫反得到 \(\sum_{k=1}^{n}2^k\sum_{d=1}^{\lfloor \frac{n}{k} \rfloor}\mu(d)\lfloor \frac{n}{kd} \rfloor^2\)。
这个式子可以直接整除分块,也可以通过
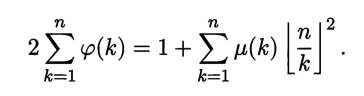
化为欧拉函数,都是 \(O(n)\) 的。
接下来是 \(va\neq vb\) 的情况,容易发现如果 \(va\) 或 \(vb\) 有一个是0或者两者符号相同都是不合法的,排除这些后让 \(va\) 和 \(vb\) 都取绝对值。
假设 \(va\perp vb\) ,否则除以他们的最大公因数。
设 \(|s|=x\times va\),\(|t|=x\times vb\),则有 \(x\leq \lfloor \frac{n}{max(va, vb)}\rfloor\),于是就是单纯的等差数列求和,即 \(\sum_{x=1}^{limit}2^x\)。
有了这些结论,剩下的就是考虑?了,设 \(a\) 中有 \(ca\) 个,\(b\) 中有 \(cb\) 个,记 \(f(x, y)\) 表示 \(va=x,vb=y\) 时上面问题的答案,那么有:
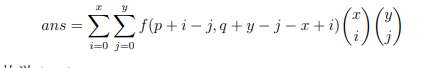
因为差值是 \(O(n)\) 的,所以考虑通过枚举差值化简,通过范德蒙德卷积的推论得到:
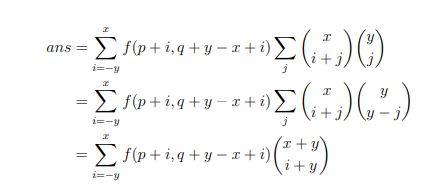
就做完了,复杂度瓶颈在上面求 \(f\) 时需要求 \(gcd\),所以是 \(O(nlogn)\)。
一些证明:
提到的莫比乌斯函数与欧拉函数间的转化:

[ARC162F] Montage
标签:计数DP
来源:ARC162订题
性质还是比较好推的,从如果左边的对角线乘积是1时右边对角线的情况如何来讨论,最终可以证明如果一个填1的位置正下方有0,那么这个0右下角都是0,四个方向类似的结论。
有一个地方在于全0行/列比较难处理,官方题解也是简单粗暴,直接删去全0行/列,那么现在问题就变成了求所有 \(a\times b\) 的矩形的数量满足左下角和右上角是1,每行每列至少有一个1,如果存在一对1的位置是左上角和右下角,那么这个小矩形内都是1。
转化成轮廓线,记录上轮廓线的到上边界的长度 \(l\),下轮廓线到下边界的长度为 \(r\),那么要求就等价于 \(l+r+1\leq b\),并且 \(l\) 上涨时不能高于上一次的 \(b-r\)。
于是可以设计DP,用 \(f_{i,l,r}\) 来表示DP到第 \(i\) 列的方案数,转移形如 \(f_{i,l,r}\rightarrow f_{i+1, l'\leq l,r'\geq r}\),并且还要注意 \(l\) 上涨时不能高于上一次的 \(b-r\)。
这个DP单次做是可以二维前缀和优化到 \(O(ab^2)\) 的,通过枚举 \(a\leq n, b\leq m\) 后复杂度是 \(O(n^2m^3)\),不能接受。
实际上我们不需要考虑 \(a,b\) 具体是什么,可以假设 \(b=m\),那么更新答案的时候因为要求右上角是0,所以更新到 \(m-l\) 的位置即可,相当于认为强行把上轮廓线与上边界重合。
于是就做完了,最后乘一下选出来 \(a,b\) 的方案即可,即 \(C_{n}^{a}C_{m}^{b}\)。
时间复杂度 \(O(nm^2)\),空间可以做到 \(O(m^2)\)。
6.24
CF1296E String Coloring
标签:Dilworth 定理
来源:?
被 Dilworth 定理橄榄了,借这道简单的应用题稍微整理一下。
Dilworth 定理是应用在偏序集上的,用来转化偏序集的最大/小反链覆盖问题。
在OI中主要应用在图论或者可以转化到图论上的问题,那么元素间的偏序关系就可以看做两个点间的有向边。
一些定义:
链:称一个点集为链,当且仅当对于链上的任意两点 \(x,y\),存在 \(x\) 到 \(y\) 或 \(y\) 到 \(x\) 的路径。
反链:称一个点集为反链,当且仅当对于链上的任意两点,不存在任何从 \(x\) 到 \(y\) 或从 \(y\) 到 \(x\) 的路径。
那么根据 Dilworth 定理,有最小反链覆盖=最长链,最小链覆盖=最长反链,常见的是前者,并且常见的是在DAG上求最长链。
回到这题,不难看出元素是下标,偏序关系是两个下标字符值的大小,那么问题就转化为了求这个有向图上的最小链覆盖,这里的链实际上就是最长非严格递增子序列。
那么根据 Dilworth 定理,就变成了求最长反链,对应的就是最长严格下降子序列,第一问解决。
那么构造也是简单的,只需要倒着做DP,把每个点的颜色赋为以它结尾的最长严格下降子序列的长度即可,证明考虑把颜色相同的划分到一条链上,也就是非严格递增子序列中。
于是就做完了,复杂度 \(O(26\times n)\)。
看到最小化划分的数量这种的,很有可能就和 Dilworth 有关,先要抓住偏序集的定义,找到元素和偏序关系,然后再分析原问题的覆盖是链还是反链做进一步的转化。
POJ1065 Wooden Sticks
标签:Dilworth 定理,贪心
来源:?
这题的偏序关系题目已经明显给出了,题意也很容易看出来是求最小链覆盖,于是要求解最长反链。
一开始觉得最长反链跟补图最大团差不多,因为原图是传递闭包的DAG,就直接拆点二分图直接做DAG最小路径覆盖,复杂度 \(O(n^{2.5})\),轻松TLE。
回过头想一下,不难想到任何一条反链按照优先第一维升序,相同时第二维降序,整体看第二维一定是个严格递减序列,证明可以考虑反证法。
于是把所有元素按第一维排序,跑一个LDS即可,可以做到 \(O(nlogn)\),不过原题数据范围 \(O(n^2)\) 也是能过的。
PS:POJ3636 Nested Dolls和这题几乎一样,只需要注意排序的偏序关系。
[ABC236Ex] Distinct Multiples
标签:计数DP,容斥,状压DP
来源:?
很妙的容斥,和这题很像。
考虑建一个有 \(n\) 个点的图,如果两个点的数字相等就连一条边,这张图所有的边都有可能出现,定义一个边集 \(S\) 的答案是 \(f(S)\),那么要求的容斥一下就是 \(\sum_{S}(-1)^{|S|}f(S)\)。
直接枚举边集计算复杂度起码是 \(O(2^{C_{n}^{2}})\) 的,不能接受,考虑把边放到点上。
定义 \(g(T)\) 表示 \(\lfloor \frac{m}{lcm_{i\in T}d_i} \rfloor\),也就是要求点集内填的数字都是相同的。
为了方便求答案,定义 \(dp(T)\) 为仅考虑点集 \(T\) 形成的边集 \(S'\) 的 \(\sum_{S\subset S'}f(S)\),按套路枚举点集内某个点所在的点集切割掉,得到 \(dp(T)=\sum_{T'\subset T,u\in T'}g(T')h(T')dp(T\setminus T')\),其中 \(h(T)\) 表示点集 \(T\) 的边集 \(S''\) 的 \(\sum_{S\in S''}(-1)^{|S|}\),这里要求边集 \(S\) 必须使 \(T\) 连通,否则就失去了切割点集的意义。
考虑对于 \(|T|\) 相等的 \(T\),在本题中相当于都是完全图,所以他们的 \(h(T)\) 是相等的,只需要考虑 \(h(|T|)\) 即可。
首先一定有 \(h(1)=1\),接下来考虑 \(h(i\geq 2)\)。
必须连通很困难,而根据二项式定理我们知道 \(\sum_{S\subset T}(-1)^{|S|}=[|T|=1]\),所以在 \(i\geq 2\) 时不考虑必须连通的容斥系数和是0,因此可以通过计算不连通的取补集。
考虑枚举某个点所在的点集大小 \(j\),不难发现如果 \(j\leq i-2\),那么新增奇数条边和新增偶数条边的方案数相等,互相抵消,所以只需要考虑 \(j=i-1\) 的情况,因为必须含有钦定的点,所以有 \(n-1\) 种,每种都是新增了一个点,所以有递推式 \(h(i)=0-(i-1)h(i-1)\)。
于是 \(h\) 可以 \(O(n)\) 预处理,\(g\) 可以 \(O(n2^nlogm)\) 预处理,做DP是枚举子集的复杂度也就是 \(O(3^n)\),可以通过。
bonus:如果像开头提到的那题一样是通过给定边的方式指定一些点对不能相等,应该也是可以做的,处理 \(h\) 的复杂度会高一些。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号