Binary Search Tree 1（EOlymp - 4146、AVL模板题）

题面

题目链接：传送门

题意

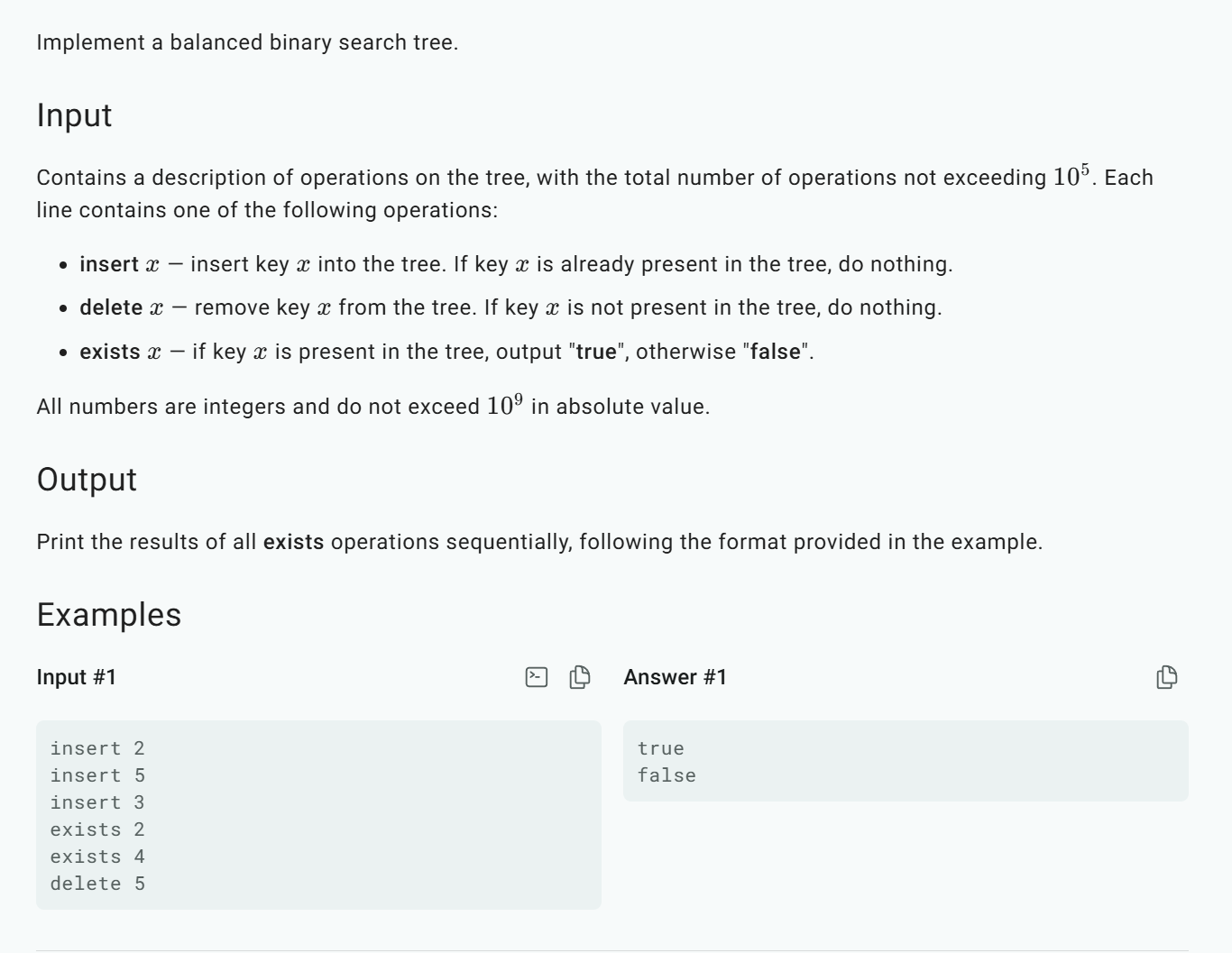
实现一棵bst的插入、删除、查找功能

思路

可以用set之类的模拟，但最近在学avl，所以就来调试avl模板

代码

#include <cmath>
#include <queue>
#include <cstdio>
#include <string>
#include <iostream>
using namespace std;

typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
 
#define fi first
#define se second
#define lson (rt<<1)
#define rson (rt<<1|1)
#define lowbit(x) (x&(-x))
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]"<<endl
#define FIN freopen("./in.txt","r",stdin)
 
const double eps = 1e-8;
const int mod = 1000000007;
const int maxn = 1000000 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;

int x;
char op[10];

#define stature(x) (x ? (x)->_h : -1 ) // 节点高度，空节点高度为-1
#define BalFal(x) (stature(x->lc) - stature(x->rc)) // 平衡因子
#define AVLBalance(x) (BalFal(x) >= -1 && BalFal(x) <= 1) // avl平衡条件
// 儿子中较高者，如果左右子树树高相等则优先考虑和父节点同方向的儿子
#define tallerChild(x) (\
    stature(x->lc) < stature(x->rc) ? x->rc : (\
    stature(x->lc) > stature(x->rc) ? x->lc : (\
    (x->fa && x->fa->lc == x) ? x->lc : x->rc\
)\
)\
)
// 获取来自父亲的引用，以保证与其他部分连通
#define FromParentTo(x, _root) ( (x->fa) ? (x->fa->lc == x ? x->fa->lc : x->fa->rc) : _root)

template <typename T>
struct AVLNode {
    T val;
    int _h;
    AVLNode *fa, *lc, *rc;

    AVLNode(T v, int h = 0, AVLNode *f = nullptr, AVLNode *l = nullptr, AVLNode *r = nullptr) : val(v), _h(h), fa(f), lc(l), rc(r) {}

    void updateHeight() {
        _h = 1 + max(stature(lc), stature(rc));
    }

    bool operator == (const AVLNode* x) const {
        return val == x.val;
    }

    void updateHeightAbove() {
        updateHeight();
        if (fa) fa->updateHeightAbove();
    }

    AVLNode* Succ() {
        AVLNode *ret = this;
        if (ret->rc) {
            ret = ret->rc;
            while (ret->lc) {
                ret = ret->lc;
            }
        } else {
            while (ret->fa && ret == ret->fa->rc) {
                ret = ret->fa;
            }
            ret = ret->fa;
        }
        return ret;
    }
};

template <typename T>
class AVL {
    AVLNode<T> *_root;
    AVLNode<T> *_hot;

public:
    AVL(AVLNode<T> *r = nullptr) : _root(r) { _hot = nullptr; }

    ~AVL() {
        destory(_root);
    }

    void destory(AVLNode<T> *cur) {
        if (!cur) return;
        destory(cur->lc);
        destory(cur->rc);
        delete cur;
    }

    AVLNode<T>*& search(const T& e) {
        if (!_root || _root->val == e) {
            _hot = nullptr;
            return _root;
        }
        _hot = _root;
        while (true) {
            AVLNode<T> *&ret = e < _hot->val ? _hot->lc : _hot->rc;
            if (!ret || ret->val == e) return ret;
            _hot = ret;
        }
    }

    void connect34(AVLNode<T> *a, AVLNode<T> *b, AVLNode<T> *c, AVLNode<T> *T0, AVLNode<T> *T1, AVLNode<T> *T2, AVLNode<T> *T3) {
        a->lc = T0;
        if (T0) T0->fa = a;
        a->rc = T1;
        if (T1) T1->fa = a;
        a->updateHeight();

        c->lc = T2;
        if (T2) T2->fa = c;
        c->rc = T3;
        if (T3) T3->fa = c;
        c->updateHeight();

        b->lc = a, a->fa = b;
        b->rc = c, c->fa = b;
        b->updateHeight();
    }

    void rotate(AVLNode<T> *v) {
        AVLNode<T> *p = v->fa, *g = p->fa;
        int turnV = v == p->rc;
        int turnP = p == g->rc;

        AVLNode<T> *r = (turnP == turnV) ? p : v; // 旋转后子树的根节点
        (FromParentTo(g, _root) = r)->fa = g->fa;

        switch ((turnP << 1) | turnV) {
            case 0b00:
                connect34(v, p, g, v->lc, v->rc, p->rc, g->rc);
                break;
            case 0b01:
                connect34(p, v, g, p->lc, v->lc, v->rc, g->rc);
                break;
            case 0b10:
                connect34(g, v, p, g->lc, v->lc, v->rc, p->rc);
                break;
            default:
                connect34(g, p, v, g->lc, p->lc, v->lc, v->rc);
                break;
        }
    }

    AVLNode<T>* insert(const T& e) {
        AVLNode<T> *&ret = search(e);
        if (ret) return ret;
        AVLNode<T> *xx =  ret = new AVLNode<T>(e, 0, _hot);

        for (AVLNode<T> *g = _hot; g; g->updateHeight(), g = g->fa) {
            if (!AVLBalance(g)) {
                rotate(tallerChild(tallerChild(g)));
                break;
            }
        }

        return ret;
    }

    void removeAt(AVLNode<T> *&x, AVLNode<T> *&hot) {
        AVLNode<T> *w = x;
        AVLNode<T> *succ = nullptr;
        if ( !x->lc )
            succ = x = x->rc;
        else if ( !x->rc )
            succ = x = x->lc;
        else {
           w = w->Succ();
           swap( x->val, w->val );
           AVLNode<T> *u = w->fa;
           ( ( u == x ) ? u->rc : u->lc ) = succ = w->rc;
        }
        hot = w->fa;
        if ( succ ) succ->fa = hot;
        delete w;
    }

    void remove(const T& e) {
        AVLNode<T> *&fd = search(e);
        if (!fd) return;

        removeAt(fd, _hot);

        for (AVLNode<T> *g = _hot; g; g->updateHeight(), g = g->fa) {
            if (!AVLBalance(g)) {
                rotate(tallerChild(tallerChild(g)));
            }
        }
    }
};

int main(){
    AVL<int> avl;
    while (~scanf("%s%d", op, &x)) {
        if (op[0] == 'i') {
            avl.insert(x);
        } else if (op[0] == 'd') {
            avl.remove(x);
        } else {
            if (avl.search(x)) printf("true\n");
            else printf("false\n");
        }
    }
    return 0;
}